導讀
文章總結了降低Transformer模型復雜度的方法,包括Softmax Attention的計算復雜度、稀疏Attention方法等。
Transformer最重要的特性是Global Interaction,也就是說對于任意兩個位置的token(不論它們離的有多遠),它們之間都能直接進行信息交互。這個特性解決了傳統序列建模中長依賴的問題。
但Transformer也有一個典型問題:它的計算復雜度和空間復雜度均為 , 其中 為序列長度。
因此實際應用中很難將Transformer應用到長序列任務上,如包數萬個token的論文閱讀、書籍閱讀等任務。
解決Transformer計算復雜度的方法多種多樣。本文介紹其中最主流、最常見的一些方法。
Note:
為簡化,本文不單獨討論multi-head的情況。大多數方法都可以平移到到multi-head中。
本文主要討論Transformer的Decoder。通常Encoder和Decoder的唯一區別是Encoder中當前token可以attend到左邊和右邊的其它token,而Decoder中當前token只能attend到左邊token。所以本文介紹的這些方法都可以輕易地擴展到Encoder中。
1. Transformer的計算復雜度
首先來詳細說明為什么Transformer的計算復雜度是 。將Transformer中標準的Attention稱為Softmax Attention。令 為長度為 的序列, 其維度為 , 。 可看作Softmax Attention的輸入。
Softmax Attention首先使用線性變換將輸入 變換為Query、Key和Value:
(1)
(2)
(3)
其中 和 都是待訓練的參數矩陣; 是 和 的維度; 是 的維度。由此可得 的shape分別為:
(4)
(5)
(6)
在常見的Transformer中, 通常 。因此為了簡化符號, 我們假設后文中 , 并且只用符號 (Dimension)。
有了Q、K、V, Softmax Attention(SA)的計算如下:
(7)
容易看到,Softmax Attention的計算主要包含兩次矩陣乘法操作。
首先回憶一下矩陣乘法的計算復雜度。對于矩陣 和 , 它們的矩陣乘法共需要 次乘法運算。可以拿國內線性代數教材使用最多的計算方法來理解:為了計算這兩個矩陣的乘積, 需要拿矩陣 的每一行去與矩陣 的每一列做點積。因此總共需要 次點積。每次點積包含 次乘法和 次加法。考慮到加法復雜度遠小于乘法, 所以總的計算復雜度就是 。
這個 可以使用兩種方法理解:
第一種理解方法, 因為加法復雜度遠小于乘法, 所以忽略加法, 那么 計算復雜度中的base operator指的是乘法操作。
第二種理解方法, 因為 與 的量級一致, 所以 計算復雜度中的base operator 指的是乘加操作 (乘法和加法) 。
回到Transformer的復雜度問題上,前面提到Softmax Attention的計算主要包含兩次矩陣乘法操作。
第一次矩陣乘法是 , 結合上文關于矩陣乘法復雜度的結論和這兩個矩陣的大小(公式 (4)和公式(5)),可知 的復雜度為 。
第二次矩陣乘法是 sof tmax 的結果與 的乘積。sof tmax 輸出的矩陣大小為 , 矩陣 的大小為 (公式(6), 前文假設了 ), 所以這一次矩陣乘法的復雜度為 。
因為這兩次矩陣乘法是順序執行的, 所以總的復雜度為它們各自復雜度之和。因為這兩個復雜度相等, 相加只是引入了一個常數項, 所以可以忽略, 因此Softmax Attention總的復雜度就為
當我們只關心復雜度與序列長度 之間的關系時, 可以忽略 并將其寫為 。
這就是通常說的Transformer計算復雜度隨序列長度呈二次方增長的由來。容易看到,Transformer的空間復雜隨序列長度也呈二次方增長,即空間復雜度也為 。
這一節最后,我們用一幅簡單的圖來說明Softmax Attention中參與每個token的Attention Score計算的其它token的位置(只考慮Decoder)。該圖主要是為了與后文的一些其它復雜方法作對比。
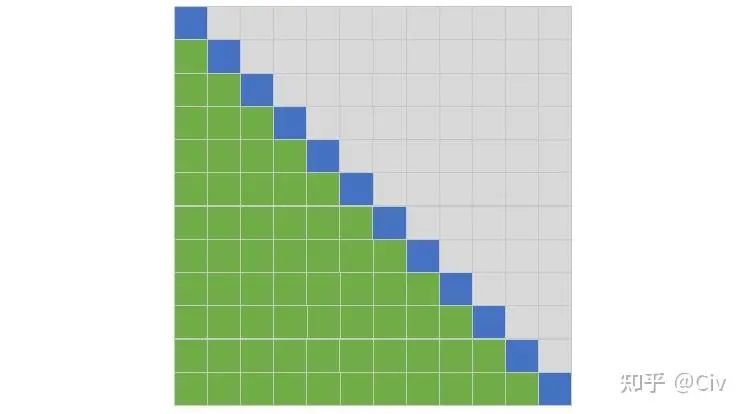
圖1 Softmax Attention中參與每個token的Attention Score計算的其它token的位置
這幅圖按如下方法理解:行和列都表示位置;藍色表示當前token,綠色表示參與當前token計算的其它token的位置。
例如,圖中有12行,可以看作該示例中序列長度為12。以第二行為例,它表示對于第二個位置的token(藍色位置,當前token),只有第一個位置的token會參與它Attention Score的計算。這其實就是Transformer中Decoder采用的方式:只能看當前token左邊的token。
為了簡化表述,后文會使用如下方式來表述:第二行中,第二個token只能attend到第一個token。
同理,在第三行中,第三個token可以attend到第一個和第二個token。
以此類推。
同時,也會采用被動表述。例如,在第二行中,第一個token被attended到第二個token。此時,第一個token也可以被稱為attended token。
2. Sparse Attention
再看一次圖1中的Softmax Attention,容易看到對于每一個token,它都會attend到它前面的所有token。所以通常說Softmax Attention是密集的(dense)。
與密集相對的就是稀疏(Sparse)了。Sparse Attention的主要思路是減少每個token需要attend的token數量。
比如,Softmax Attention對于每個token都要attend它之前的所有token。那么為了減少計算量,能不能只去attend之前的部分token?
2.1 Factorized Self-Attention (Sparse Transformer)
Paper:Generating Long Sequences with Sparse Transformers (2019)
Key Contribution:提出了兩種稀疏Attention方法:Strided Attention和Fixed Attention。這二者均可將Transformer的 復雜度降低至 。
Factorized Self-Attention的一個基礎假設是:在Softmax Attention中,真正為目標token提供信息的attended token非常少。
換言之,該假設意味著:對于Softmax Attention,在經softmax得到的Attention Weights中,其中大部分的值都趨于0,只有少數值明顯大于0。因此Attention Weight比較稀疏。
論文作者將Transformer用到了圖像自回歸任務中來表明他們假設的合理性,如圖2.1.1所示(圖2.1.1不容易懂,看后文解釋)。

圖2.1.1 Softmax Attention中Weight Vector稀疏性示意圖
解釋一下圖2.1.1。作者們用了128層的Transformer在CIFRA-10上做自回歸訓練。自回歸訓練是逐行逐像素來做的。
以圖a)中左上方的紅色汽車圖為例,圖中黑色區域(下方)是mask。模型下一步需要去預測mask中的第一個點。所謂第一個點,就是逐行看,看到的一個mask黑色點。圖中白色區域是Attention Weights。可以看到,有效的Attention Weights幾乎全部集中在當前待預測點周圍。所以此時的Attention Weights很像卷積的局部性。同時它也很稀疏,因為Attention Weights在較遠的位置幾乎全為0。
圖2中a、b、c、d是來自不同網絡層的Attention Weights。可以看到,雖然Attention Weights表現出的空間規律有所差異,但它們總體上都很稀疏:只有極少部分的位置被有效attend(Attention Weights明顯大于0,即圖中白色區域)。
基于這種稀疏性,作者們提出了兩種Attention方法。
注:針對這篇paper的Attention方法,本文不列具體公式。這是因為,這些方法其實都非常簡單,但公式反而繁瑣、不直觀。
第一種方法稱為Strided Attention。它又由兩種Attention機制構成,我們把它們分別記為SA1和SA2(原文沒有這種命名法,這里只是為了指代方便):
SA1: 每個token只能Attend它左邊相鄰的L個token。
SA2:每個token只能Attend它左邊部分token,這些attened token用如下方法選出:從自己開始往左邊數,每隔L就會有一個token可以attend(參見圖2.1.3,比較直觀)。
為便于理解,請參見圖2.1.2和圖2.1.3,我們假設L=3。

圖2.1.2 Strided Attention的SA1。圖中每個token只能attend到它左邊相鄰的L個token,圖中L=3。

圖2.1.3 Strided Attention的SA2,圖中L=3。
圖2.1.2中的SA1很容易理解,每一個當前token(每一行的藍色區域)只能attend到它左邊的L個token,圖中L=3。圖2.1.3中的SA2稍微復雜一點,從自己開始往左邊數,每隔L就會有一個token可以attend。比如圖2.1.3中最后一行,從當前token(藍色區域)開始往左邊數,相隔L個空格(3個空格)處遇到第一個綠色方塊可以attend(最后一行,第8列),然后再往左數L個(3個)空格,遇到第二個綠色方塊可以attend(最后一行,第4列),以此類推。
Strided Attention的SA1方法和SA2方法的本質是在選擇哪些token可以attend。
然后我們來看這兩種Attention方法怎么用在Transformer結構中。有三種方法:
交替使用。在第1個Transformer Block中使用SA1,然后在第2個Transformer Block中使用SA2,然后在第3個Transformer Block中又使用SA1,在第4個Transformer Block中又使用SA2,以此類推。這種方法能work的原因是:雖然SA1只能看左邊的L個相鄰位置,但可以認為在SA1中,每個token聚合了它左邊L個token的信息。因此在SA2,雖然它是跳著L個位置看的,但整體感受野等價于整個序列(因為每個attended token聚合了其左邊L個token的信息)。
聯合使用。將SA1選擇的attended token和SA2選擇的attended token合在一起使用。這個方法很簡單,就是在計算Attention時,首先用SA1去選擇一些token,再用SA2去選擇一些token,然后計算Attention時只使用選擇出的token參與計算即可。
多頭使用。類似Transformer采用的多頭機制,這里每個頭可以使用SA1、SA2或Transformer中的Softmax Attention。
然后來看 的選擇。只要將 的值設為 , 那么容易看到整個Strided Attention的計算復雜度就是 。雖然這個做法很不自然, 但是它確實能實現 的復雜度。
至此,我們介紹完了Strided Attention。
作者們提出的第二種Attention稱為Fixed Attention。Fixed Attention也有兩種機制,將它們分別稱為FA1和FA2。為了便于理解,需要把這兩種機制畫到一個圖里,如圖2.1.4所示。
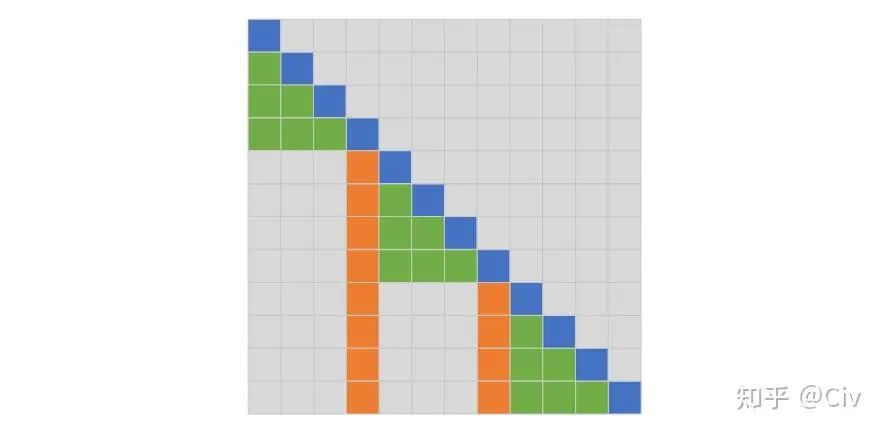
圖2.1.4 Fixed Attention中的FA1(綠色)和FA2(橙色),L=3
先看FA2,如圖中橙色區域。橙色區域的位置是固定的,即從左往右數,每隔L個位置,選中一個token。
理解了FA2,FA1的選擇方式就會容易理解了。對于每個當前token(藍色),往它左邊遍歷(綠色),直到遇到第一個FA2選中的token(橙色)。
Fixed Attention的使用方法和上文介紹的Strided Attention的三種方法一致(交替使用、聯合使用、多頭使用),不再贅述。
作者們的結論:Strided Attention適用于圖像、音頻;Fixed Attention適用于文本。
理由如下:Strided Attention在attended token的位置上做了強假設:哪些位置的token應該被attened,與當前token位置強相關。作者們認為這種適合圖像、音頻這類數據。而在文本上這類假設不成立。所以在Fixed Attention中,哪些位置的token應該被attened,與當前token位置無關。
講的再簡單點,圖像、音頻的局部信息很重要;而文本全局信息更重要。
總結:paper對新手不友好,簡單的事情用了公式來解釋,非常繁瑣。希望本文能比原文容易理解一點。
2.2 Blockwise Self-Attention
Paper:Blockwise Self-Attention for Long Document Understanding (2019)
Key Contribution:通過分塊來降低Softmax Attention的計算復雜度,方法簡單,且實驗效果較好。
前文提到了Transformer的時間復雜度和空間復雜度都為。Blockwise Self-Attention這篇Paper對空間復雜度做了更細致的分析。
一個模型的Memory Usage主要來自三部分:Model Memory、Optimizer Memory、Activation Memory。按照Transformer模型通常使用的Adam類優化器來看,Optimizer Memory是Model Memory的三倍。這是因為Optimizer Memory需要為每個參數存儲梯度、first momentum和second momentum。
Model Memory和Optimizer Memory可以直接計算出來。比如對于Model Memory,可以直接通過模型大小與參數類型(如FP16、FP32、INT8)來推算出精確值。同理,Optimizer Memory也可以精確計算出。而Activation Memory則與具體實現相關。所以在Paper中,作者們用PyTorch的內存分析工具來看訓練時總的內存開銷,然后減去Model Memory和Optimizer Memory,以此來估算Activation Memory。
作者們以BERT-base為例,分析了Model Memory、Optimizer Memory、Activation Memory三者的占比,其中Activation Memory獨占87.6%,屬于內存開銷最大的部分。畫一幅圖來總結上面提到的內容(注意圖中的memory usage的比例是針對BERT-base而言的):

圖2.2.1 BERT-base中內存分布示意圖
我們說的空間復雜度 主要指的就是Activation Memory這一部分。因為Model Memory和Optimizer Memory是線性復雜度 。
Blockwise Self-Attention的核心思想非常簡單:將一個長度為N的序列,平均分成n個短序列。當原始序列長度N無法被n除盡時,對原始序列進行padding,使它能被除盡。舉一個例子來說明Blockwise Self-Attention的計算過程。
假設序列長度 , 每個token的維度為 。在Transformer中, Q、K、V三個矩陣的大小都為 。在Blockwise Self-Attention中, 假設分塊數 , 那么每個分塊中的序列長度為 。所以輸入序列 可以劃分為 個子序列: 、 , 它們的大小都為 。同理可以把 ( 同理) 劃分成 個子矩陣:、 , 它們的大小也都為 。在計算Self-Attention時, 每個 會去選擇一個 和 來計算:(2.2.1)
在只有一個Attention頭的情況下, 選擇 和 的方法是:shifting one position。很簡單, 選擇 和 選擇 和 選擇 和 。換言之, 始終選下一個 和 ; 當 是最后一個block時, 選擇 和 。這個過程可以用取余數的符號寫出來, 但看著太繁瑣, 所以文字描述了。
多頭Attention情況下稍微麻煩一點。我們記序列 為單頭Attention情況下每個 對應的 和 的編號 :(2.2.2)
仍以上面的示例為例, 在單頭情況下, 的值為:(2.2.3)
它表示, 對應的 的值是2, 對應的 的值是 對應的 的值是1。
在多頭情況下, 第 個頭的 定義如下:(2.2.4)
例如, 按照上述示例, 第一個頭的 為:(2.2.5)
第二個頭的 為:(2.2.6)
因為分塊數 , 所以需要取余數(注意下標從1開始, 所以余 0 時替換為 即可),得到最終的結果:(2.2.7)
過程其實很簡單, 只是寫出來稍微麻煩一點。
最后來分析復雜度。由本文第一部分分析Transformer復雜度的結論可知, 公式(2.2.1)中的復雜度為 。因為對每一個分塊, 都需要用公式 (2.2.1) 進行計算, 所以總復雜度為:(2.2.8)
這既是計算復雜度,也是空間復雜度。
在原文中, 通常選為2。注意, 在大 計法中一般會忽略掉常數項。所以在這種意義下, Blockwise Self-Attention的復雜度仍為 。
但是大 計法的主要目的是理論分析, 并不為實際工程優化。所以即使在大 意義下復雜度沒有變, 但它實際計算量仍然減少了。沒有改變的 仍然意味著,Blockwise Self-Attention不能擴展到太大的 上,這就是大 計法的作用。
具體來看, 當 時, RoBERTa的訓練時間由原來的9.7天減少至7.5天。
總結:相比于Sparse Transformer中的Factorized Self-Attention,Blockwise Self-Attention更簡單,且從效果上來看,優于Factorized Self-Attention。
2.3 Longformer
paper:Longformer: The Long-Document Transformer (2020)
Key Contribution:設計了多種不同的Local Attention和Global Attention方法。
首先重新看一下Factorized Self-Attention (2.1小節)中的兩種Attention方法:Strided Attention和Fixed Attention。在Strided Attention中,又有兩種Attention機制,在前文中我們把它們分別稱為SA1和SA2(參考圖2.1.2和2.1.3)。SA1的作用是Local Interaction,而SA2的作用是Global Interation。類似的,在Fixed Attention中(參考圖2.1.4),FA1的作用是Local Interaction,而FA2的作用是Global Interation。
在Factorized Self-Attention中,它主要依靠兩類Attention的組合使用來實現長距離依賴,例如SA1+SA2(或FA1+FA2)。
Longformer的核心idea和Factorized Self-Attention很像,只是Longformer中的部分Attention只有Local Interaction,沒有Global Interaction。
Longformer一共提出了三種Attention,分別是SlidingWindow basedAttention(SW-Attention)、DilatedSlidingWindow basedAttention(DSW-Attention)和GlobalAttention(G-Attention)。下面分別介紹。
先看SlidingWindow basedAttention(SW-Attention),它其實和Strided Attention中的SA1完全一樣。為了方便大家查看,重新把Strided Attention的SA1圖copy一份到此處。

圖2.3.1 SW-Attention示意圖,它和Strided Attention中的SA1完全一樣。圖中L=3
SW-Attention只Attend它左邊的L個token。在SW-Attention中,L被稱為“窗口大小”,而在Strided Attention中,L被稱為“步長(Stride)”,它們本質一樣。
實際上我們可以在Transformer中只使用SW-Attention來構建具有Global Interaction的網絡。其方法很簡單,只需要堆疊多個SW-Attention網絡層即可,就如同CNN增大感受野的方式。假設窗口大小為K,一個M層的SW-Attention結構中最頂層的“感受野”大小為KM,如圖2.3.2所示。
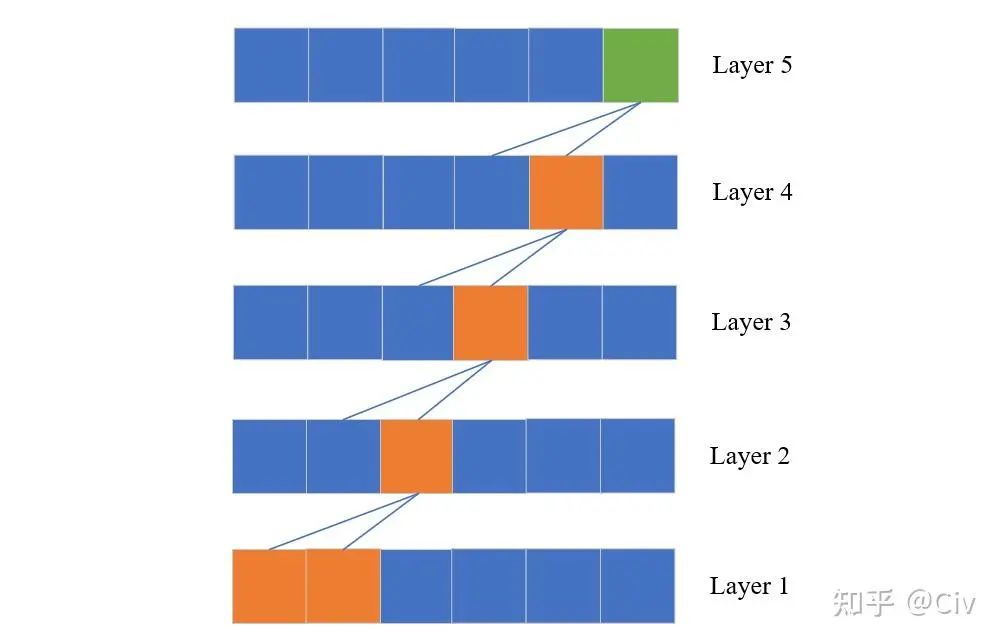
圖2.3.2 基于SW-Attention構建的Transformer的Global Interaction示意圖
圖中綠色方塊表示當前token;藍色線表示信息流;每一層是上一層的輸入;L假設為2。在第一層中,第一個token和第二個token的信息會流入第二層中的第三個token。而在第二層中,第二個token和第三個token的信息會流入下一層中的第四個token,以此類推。在最頂層(第五層),雖然當前token的信息只來自上一層的第四個token和第五個token,但從信息流的角度來看,它也隱含包含第一層中第一個和第二個token的信息。
可以看到,通過堆疊SW-Attention,Transformer也可以像CNN一樣增加感受野。但是很容易想到,這種非常“間接”的方法不會有太好效果,就像CNN對長依賴建模的能力比較差一樣。
再來看DilatedSlidingWindow basedAttention(DSW-Attention),它其實和Strided Attention中的SA2完全一樣。為了方便大家查看,重新把Strided Attention的SA2圖copy一份到此處。

圖2.3.3 DSW-Attention示意圖,它和Strided Attention中的SA2完全一樣。圖中Dilation=3。
DSW-Attention是“空洞”版的SW-Attention,就像空洞卷積和卷積之間的關系。簡單來說,被attended的token不再像SW-Attention中是連續排列的,而是按等間距排列(間距稱為“空洞率”,在圖2.3.3中為3)。
與SW-Attention類似,通過堆疊多個DSW-Attention也能增大網絡的感受野,從而實現Global Interaction。
最后再來看GlobalAttention(G-Attention)。G-Attention是SW-Attention的改進版,它的主要改動是:在SW-Attention基礎上,增加了部分固定位置,使得這些位置的token需要 1)attend到其它所有token;2)被其它位置tokenattend到。如圖2.3.4所示。
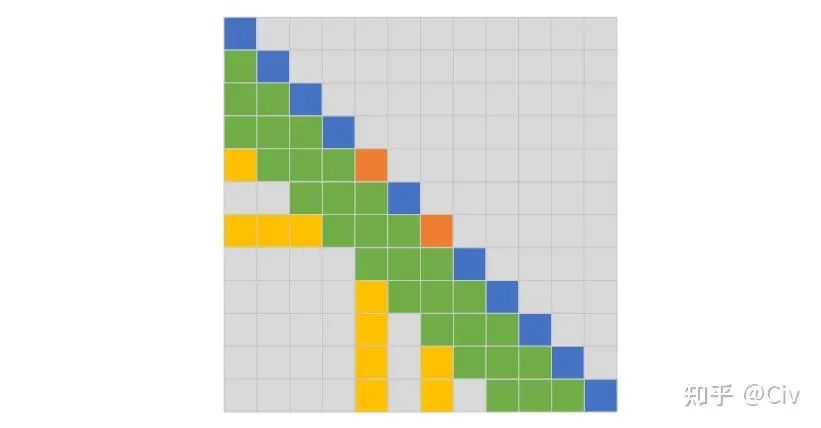
圖2.3.4 G-Attention示意圖,L=3
圖中綠色token是SW-Attention會attend到的token。橙色token是在G-Attention中額外選中的token。以第五行的當前token為例(橙色),因為它是被額外選中的token,所以它會attend它左邊的所有token。圖中用黃色標出了相對于SW-Attention之外的額外被attended的token。此外,其它所有token也需要attend到第五個token,參見圖中最后四行中的靠左黃色列。
圖中第7行類似,大家可以自行對照圖腦補一下這個過程。
在G-Attention中,哪些位置會被額外選中與具體下游任務相關。例如,在分類任務中,[CLS] token會被額外選中(Longformer一文中以RoBERTa為基礎,將其中的Attention改為本文提到的Attention中的一種或多種);在問答任務中,所有問題的token都會被額外選中。
此外,G-Attention中有兩份不同的QKV,一份用于計算由SW-Attention選中的token(圖2.3.4中的綠色token),另一份用于計算由G-Attention額外選中的token(圖2.3.4中的黃色token)。
上述提到的三種Attention的復雜度都為 , 因為哪些token會被attend與序列長度 無關。
2.4 Local attention and Memory-compressed attention
Paper: Generating wikipedia by summarizing long sequences (2018)
Key Contribution: 提出了Local Attention和Memory-compressed attention。Local Attention的計算復雜度隨序列長度增長呈線性增長;Memory-compressed attention可以將計算復雜度減少固定常數倍(超參控制)。
2.4.1 Local Attention
前文中的2.3節也有一個Local Attention,但與此處的Local Attention方法不同。
此處Local Attention的核心思想是使用一個固定的分塊大小n對輸入序列進行分塊,并限制self-attention的計算只能在各個分塊內單獨進行,如圖2.4.1所示。
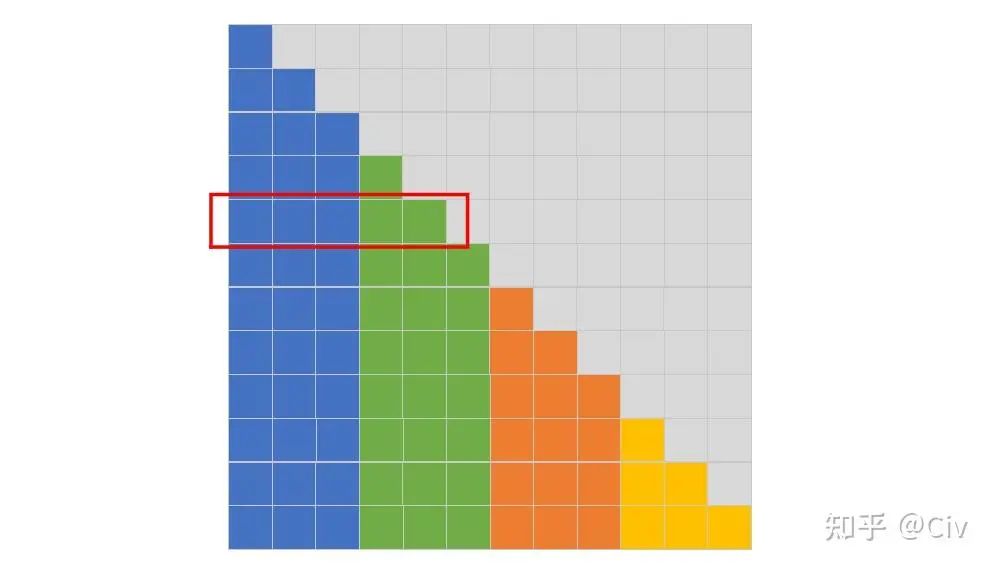
圖2.4.1 Local Attention的模式圖。圖中假設序列長度N=12,分塊大小n=3。
在圖2.4.1中,每個位置的token只能attend到與它同顏色的其它token。例如圖中第五行(紅色標注行),它表示在Decoder結構中,對于輸入序列中的第5個token的attention模式:第五行的灰色區域表示mask,這些mask表示Decoder結構中不能看到當前token之后的信息;前五個token根據顏色進行分塊,每個token只能attend到同分塊(同顏色)中的其它token,所以對于當前token而言(第五個token),它只能attend到第四個token和它自己(綠色部分)。
作為對比,標準的self-attention的模式圖如下:
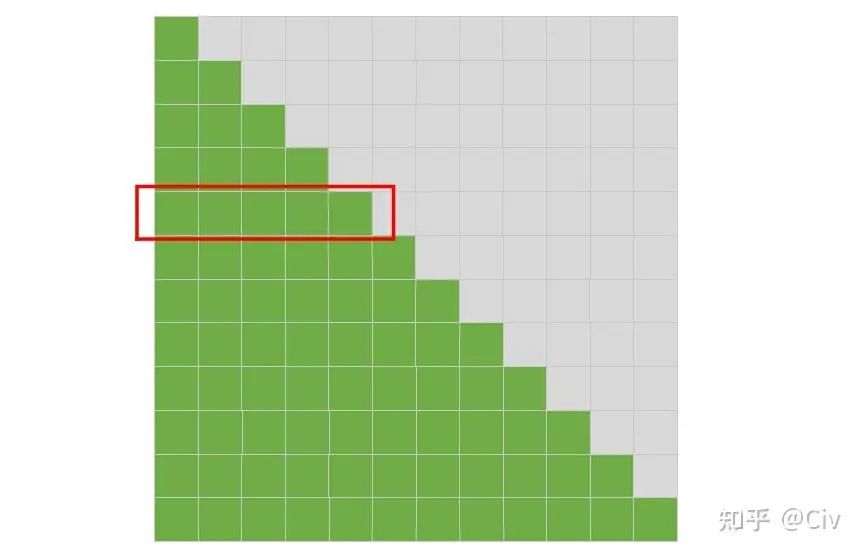
圖2.4.2 標準self-attention的模式圖。圖中假設序列長度N=12。
標準的Decoder結構中,只有一個限制:所有token都不能attend到當前序列之后的token。
Local Attention與2.2節介紹的Blockwise Self-Attention比較類似,其核心思想都是對輸入序列進行分塊。Local Attention與Blockwise Self-Attention唯一的區別是:Local Attention將Self-attention的計算限制在組內;而Blockwise Self-Attention將Self-attention的計算限制在組間。
例如,考慮圖2.4.1中的最后一行,在最簡單的情況下,Blockwise Self-Attention的attention模式為:每個分塊的token只能attend到下一個分塊(藍色token只能attend到綠色token;綠色token只能attend到橙色token;橙色token只能attend到黃色token;黃色token只能attend到藍色token)。
下面分析一下Local Attention的復雜度。Local Attention通常選擇一個固定長度的分塊大小n(例如 )。假設總的序列長度為 , 那么分塊數量為 。每一個分塊的復雜度為 個分塊的總復雜度為 。因為 為常數項, 所以Local Attention的復雜度隨序列長度 呈線性增長 。
但在2.3節中, 曾分析到Blockwise Self-Attention的復雜度是 。為何兩個如此相似的方法復雜度卻有顯著差異?
在Blockwise Self-Attention中, 的含義不是分塊大小, 而是分塊數量。所以每個分塊的大小就為 。那么每個分塊的attention計算復雜度就是 。又因一共有 個分塊, 所以總復雜度是 。
這里之所以把這兩個復雜度拿出來對比,是想說明:小心對待復雜性分析中的常量。不同視角可能會導致不同的分析結果。
復雜度唯一能體現的僅僅是:計算量與變量之間的關系。
在上面的例子中,我們關心的變量是序列長度N,所以直接忽略了常數項n。但如果我們要比較這兩個復雜度所對應的計算量時,常數項不能輕易忽略。
2.4.2 Memory-compressed Attention
在通常的基于Transformer的模型中,我們使用不同的線性變換來將輸入序列x映射為Q、K、V。這三者的尺寸通常一樣(維度一樣,長度也一樣)。
Memory-compressed Attention的思路是使用額外的卷積來降低K和V的序列長度,這樣整體Self-Attention的計算量就降低了。這樣的卷積很容易實現。假設輸入序列長度為N,維度為D,且K和V的尺寸都為[N, D]。我們只需要使用一個步長大于1的卷積,讓它沿著序列長度維度進行滑動即可,如下圖所示。
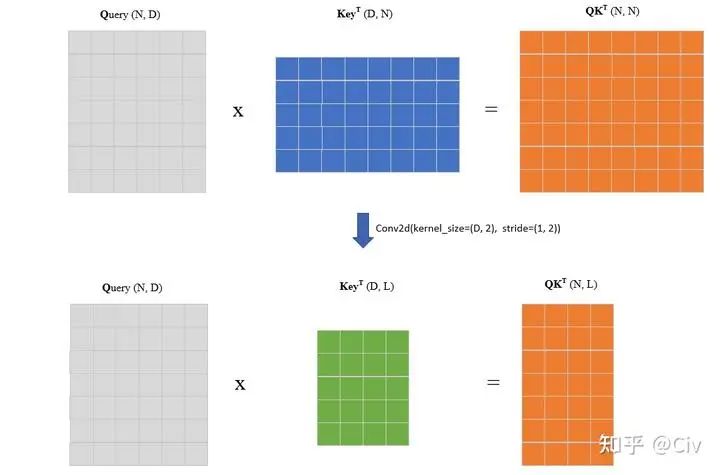
圖2.4.3 Query與Key的矩陣乘積示意圖。
圖中上部分表示標準Query與Key的計算示意圖。在Memory-compressed Attention中, 首先使用一個沿著序列長度維度滑動的卷積對該維度進行下采樣,得到一個更小的Key的矩陣,如圖中下部分所示。假設下采樣后的序列長度為 , 可知此時矩陣乘法的復雜度為 , 而標準Q、K計算的復雜度為 。一般來說, L在量級上并不會與N有明顯差異, 所以Memory-compressed Attention雖然能降低計算量, 但并不能顯著降低復雜度。
2.5 Reformer
paper: Reformer: the efficient Transformer
Key contribution: 1) 提出了LSH-attention, 能夠將Transformer的復雜度由 降低至 ;2) 將Transformer中的跳躍連接改為了“可逆跳躍連接", 這樣在網絡的前向過程中不用為后續的梯度計算存儲激活值, 能夠極大降低訓練過程的存儲開銷。
從最原始的研究動機來看,Reformer主要考慮的是:降低基于Transformer的模型在訓練階段的存儲開銷。
神經網絡在訓練過程中,最大的存儲開銷主要來自兩方面。一是網絡參數本身的存儲開銷;二是整個前向過程中產生的激活值。由存儲激活值而導致的開銷只會在訓練階段產生,因為訓練中為了計算每一層的梯度,需要用到當前層的激活值。而在推理階段,因為不需要再通過梯度信息來更新網絡,所以自然也就不用存儲每一層的激活值了。
基于這兩個部分,先來看一下基于標準Self-attention的單層Transformer的所涉及的存儲開銷:
以當時(2020年)最大的單層Transformer為例,它的參數量是0.5B。每個參數32位,也就是4Byte,所以總的內存開銷就是2GB。
假設輸入序列長度為 , embedding大小為 , batch size為 8 , 那么單個self-attention激活值所占的存儲開銷是 。同理, 每個激活值也是4Byte, 所以總的內存開銷也是 。
上述兩點涉及到的存儲開銷并不大,加起來一共也才4GB。但實際上除了這兩點,就單層Transformer而言,它還包含另外兩點最大的開銷:
在標準Transformer結構中,除了self-attention部分,在其后還有兩個全連層。兩個全連層的激活值的數量加起來通常遠大于self-attention的激活值。例如,在標準Transformer中,第一個全連層的激活值數量是self-attention的四倍,第二個全連層與self-attention相同。那么兩個全連層總的激活值就是self-attention的五倍。按照上面第二點中的計算方法,兩個全連層總的存儲開銷就是10GB。
self-attention的計算中包含 的矩陣乘法計算, 它的計算復雜度和空間復雜度都是 。例如, 當輸入序列長度為 時, 的輸出矩陣大小為 , 內存消耗約 16GB。
上述還僅僅是單層網絡的開銷(注:上述也并沒有計算完單層所有的激活開銷),對于一個N層的Transformer,這個開銷還得乘以N倍。Reformer主要采用了兩種方法來降低整體存儲開銷,分別是LSH-attention和“可逆跳躍連接”。
2.5.1 Locality-Sensitive Hashing Attention(LSH-attention)

圖2.5.1 在Self-attention中(左圖),當前token可以attend到它之前(包括自身)的所有token;LSH-attention中(右圖),當前token只attend到部分“重要”的token。
在標準的self-attention中(以decoder為例),每一個位置的token可以attend到它之前的所有token(包括它自己)。但實際上,因為softmax主要由較大的那些值所主導,所以由softmax輸出的weight vector中可能會比較稀疏。也就是說,很多位置的權重很小,只有少部分位置的權重較大。因此,一個自然的想法是不是只要找到那些產生較大權重的token即可,而不用讓所有token都參與計算?這個想法的示意如圖2.5.1所示。
在self-attention的計算中, 與當前Query越相似的Key, 它們點乘的值也會更大, 從而產生的權重也更大。為了后續描述方便, 對于某個token , 它對應的Query記為 。如果某個token 所對應的Key 能與 產生較大的點乘結果, 我們就說“token 對于token 是重要的”。
這里我們并沒有定義“較大的點乘結果”究竟是多大。這可以認為是具體策略問題, 只要使用的策略能夠區分"較大"和"不較大"就行。
LSH-attention的核心思路是, 對于當前token , 找到對它“重要的”所有token集合 , 并限制 在self-attention的計算中只能attend到集合 中的token。簡而言之, 對于當前token , 我們希望知道哪些 與 的點乘會比較大。這些 對于的token 就構成了集合 。
尋找集合 中token的本質是相似度問題。計算兩個向量相似度最簡單的辦法是計算它們的余弦相似度。但這不可取, 因為我們的目的就是為了避免計算和一些可能導致低權重的token的點乘來降低計算量。但如果為了找到它們又需要計算余弦相似度, 而余弦相似度的計算又包含點乘, 那么后續節約的計算實際上預先發生了, 所以這樣沒意義。
真正要解決的問題是找到一種高效的計算方法來判斷兩個向量是否相似。LSH-attention采用的方法是Locality sensitive hashing(局部敏感哈希)。
一個“局部敏感”的哈希算法指的是非常相似的向量具有相同的哈希值。LSH-attention使用的方法如圖2.5.2所示。
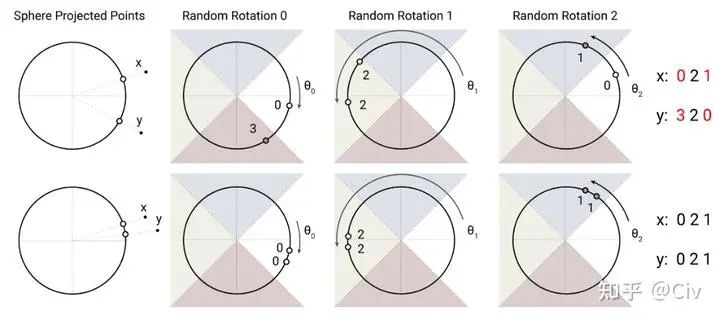
圖2.5.2 Locality sensitive hashing示意圖。圖來自原論文。
解釋一下圖2.5.2。先看圖的上半部分。假設有相距較遠的兩個點x和y,首先把它們投影到一個圓上(高維空間中對應超球面)。然后用一個隨機的旋轉將圓上的兩個投影點進行旋轉,并記錄它們落在的區域編號。圖中區域由四個不同顏色的三角形區域構成,從右沿著逆時針方向編號為0、1、2、3。所以在第一次旋轉后(對應于圖中Random Rotation 0),x落在的區域0,y落在區域3。然后再次隨機旋轉,并記錄第二次旋轉后落在的區域。圖中一共進行了三次旋轉,x分別落在區域0、2、1,因此它的哈希值就是021。而y三次分別落在區域3、2、0,所以它的哈希值是320。兩個哈希值021和320不同,那么認為x和y不相似。
圖2.5.2中的下半部分中用了兩個更接近的點作為示例,不再展開解釋了。LSH方法直覺上非常簡單,它也有一些高效的實現方法。這里簡單提一個要點:判斷一個點落在哪個區域可以通過argmax操作實現(這實際上也同時隱含地確定了空間劃分方法,但解釋起來相對麻煩,故此文不展開)。
在二維平面中,如果一個點的坐標是[x, y] (與上面例子中的x、y無關),我們可以把它擴展成一個四維向量[x, y, -x, -y]。然后對這個向量使用argmax,也就是最大值對應的索引。這個索引編號就是點[x, y]對應的區域。
要證明這點只需要注意空間的劃分是依靠y=x和y=-x這兩條線實現的即可完成。
基于LSH,整個LSH-attention的計算可由下圖描述。
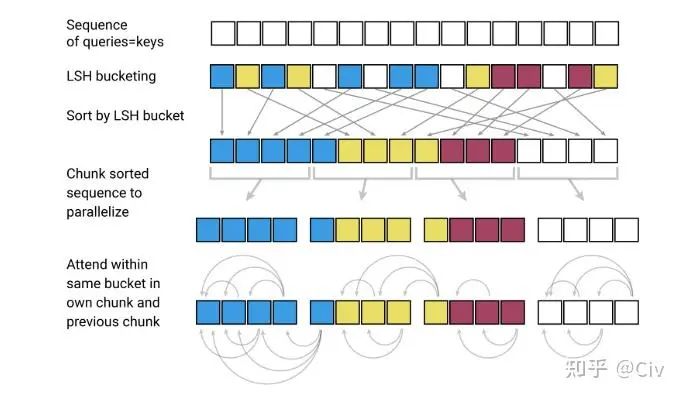
圖2.5.3 LSH-attention計算示意圖
圖2.5.3從上至下來解釋。
圖中第一行。在LSH-attention中,Query和Key是相同的,這和標準self-attention有所區別。
圖中第二行。使用LSH Hashing將token進行分組,具有相同Hash值的token被分為同一組(相同顏色表示)。
圖中第三行。按照分組對token進行重排序。同組中的token按照它們在原始序列中的位置進行排序:越靠后的排在越后面。
圖中第四行。按照固定長度對重排后的序列進行分塊。分塊的目的主要是為了并行化。
圖中第五行。每個token只能attend到同組(同顏色)之前的token。如果某個組被分成了多塊,那么后一塊中的token只能attend到前一個塊中同組的token(如果一個組被分成了三個塊,最后一個塊中的token不能attend到第一個塊中的token,即使它們是同組的)。
LSH-attention的優勢在于它降低了每一個token可以attend到的token數量。原論文中沒有詳細分析為什么LSH-attention的復雜度是 。從LSH-attention的形式來看, 它的復雜度介于 和 之間。
LSH-attention主要解決了前文中提到標準self-attention開銷中的第四點: self-attention的計算中包含 的矩陣乘法計算, 它的計算復雜度和空間復雜度都是 。例如, 當輸入序列長度為 時, 的輸出矩陣大小為 , 內存消耗約 。
2.5.2 Reversible Transformer
因為基于反向傳播的梯度計算需要用到網絡前向過程產生的激活值,所以在訓練過程中必須將這些激活值存儲起來。對于較大的模型而言,這些激活值造成的存儲開銷相當巨大。
一種樸素的解決方案是利用checkpoint。在每次反向計算過程中,當需要層i的激活值時,使用上一次的checkpoint進行一次前向計算,直到層i,然后取激活值。雖然基于checkpoint方法能在存儲不足時讓模型跑起來,但增加了太多額外計算量。
另一種方法是讓網絡變得“可逆”。也就是說,我們可以由后一層的激活值來推出前一層的激活值。基于這種方法的一個經典工作是RevNet,它讓ResNet變得可逆。
Reversible Transformer基本照搬了RevNet的思想。在整個前向過程中,網絡始終處理兩個序列 和 :(2.5.1) (2.5.2) FeedForward
輸出 和 構成下一層的輸入。對于網絡輸入層, 和 可由兩個線性層變換得到。對于任意一層, 當知道它的輸出 和 時, 利用公式 (2.5.2) 可以恢復出 :(2.5.3) FeedForward
代價是需要重新計算一次 FeedForward 。
當恢復出 后, 可以用公式(2.5.1)再恢復出 :(2.5.4)
代價是需要重新計算一次 。
如果整個網絡使用的激活函數也是可逆的,那么在前向過程中不需要存儲任何激活值。
Reformer的論文中沒有講用的激活函數是什么。在一些開源實現中有使用Gelu的,也有使用ReLU的。它們都不是可逆的激活函數。
所以對于這些激活函數而言,它們之前的輸入仍需要存儲,因為單靠激活函數的輸出無法恢復出輸入。
Reversible Transformer可以解決前文提到的第二點和第三點:
假設輸入序列長度為 , embedding大小為 , batch size為 8 , 那么單個self-attention激活值所占的存儲開銷是 。同理, 每個激活值也是4Byte, 所以總的內存開銷也是2GB。
在標準Transformer結構中,除了self-attention部分,在其后還有兩個全連層。兩個全連層的激活值的數量加起來通常遠大于self-attention的激活值。例如,在標準Transformer中,第一個全連層的激活值數量是self-attention的四倍,第二個全連層與self-attention相同。那么兩個全連層總的激活值就是self-attention的五倍。按照上面第二點中的計算方法,兩個全連層總的存儲開銷就是10GB。
2.6 Adaptive Attention
paper:Adaptive Attention Span in Transformers
Key contribution:提出了一種對不同attention head自適應選擇attention長度的方法。
在標準self-attention中,不同attention head的attention模式完全一樣,即每一個token能attend到它之前的token(包含自己)。Adaptive Attention的假設是:不同head可以具有不同的attention模式,比如有的head可能更關注較近的token,有些head可能會更注重遠距離依賴,所以可以通過學習來讓不同head自適應調整head可以attend到的token長度。
這個思路與2.5.1節中介紹的LSH-attention的相似點是都在嘗試選擇部分token來attend,以減少參與計算的總token數。區別在于,adaptive attention選擇的是一個連續的子序列,而LSH-attention沒有這個要求,如圖2.6.1所示。

圖2.6.1 LSH-attention v.s. Adaptive-attention
可以把adaptive attention理解為是在選一個“距離”:最遠可attend到的token離當前token的距離。只要這個距離確定了,那么可以被attend到的token就被確定了。
Adaptive attention的實現方法是為每一個attend到的token再加一個soft mask。下面詳細介紹。
在標準的self-attention中, 記當前token為 , 它的Query和Key分別記為 和 。對于某個目標token , 它對 的權重由如下公式計算得到:
Adaptive attention中,在計算公式(2.6.1) 中的權重時,會為每一個位置再加上一個soft mask:
簡單解釋一下。 是一個mask函數, 它的輸入是“距離”, 輸出是一個0到1的值。例如公式 (2.6.2) 的分子中, 是當前token與目標token之間的距離。mask函數 根據這個距離計算出對應的mask值。
我們說這個mask是soft的, 是因為它的輸出并不是0或1, 而是0到1, 這與平時的hard mask有所區別。
在Adaptive attention中, mask函數 定義為:
其中 是超參, 是需要學習的參數。公式很不優雅, 可以借助mask函數 的圖像來理解:
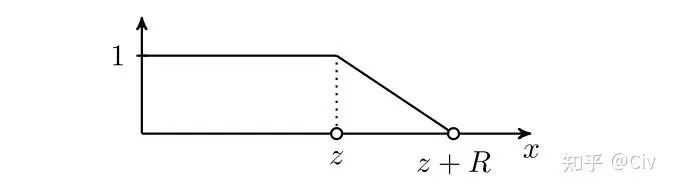
圖2.6.1 mask函數的圖像
模型會自動學習到一個合適的 , 這個 可理解為“有效token的距離”。與當前token距離 的所有token的soft mask值都為 1 , 表明它們都是有效的token。
超參數 表示一個“soft距離"。在距離 至 的范圍內, soft mask由1線性衰減到0, 表示它們的重要性逐漸降低。超過 距離的token的soft mask值為 0 , 表示它們為無效token。
對于multi-head attention中的每個head, 都需要單獨為它訓練一個 。所以不同head可以attend 到的token距離也就不同。
Adaptive attention的最核心思路就是這樣。下面再介紹兩個其它細節。
首先,Adaptive attention采用的是相對位置編碼的方法,所以公式(2.6.2)需要更改為:
(2.6.3)
其中 表示與當前token距離為 的位置編碼, 它是相對的, 且直接靠學習得到。相對位置編碼雖然簡單, 但在后續的很多其它改進版的Transformer結構中應用非常廣泛。
其次, Adaptive attention還提出了一種更復雜的參數化 的方法。在公式 (2.6.3) 中, 直接作為一個可學習參數參與訓練, 由模型直接優化。對 的一種新的參數化方法如下:
其中 表示當前token; 表示最遠可attend到的token距離, 可設置為一個期望的值, 或直接讓它等于 和 是可學習的參數; 是sigmoid函數。
公式 (2.6.4) 的含義是為每一個當前token單獨計算它的 , 而不僅僅是為每一個head計算一個
-
矩陣
+關注
關注
0文章
423瀏覽量
34548 -
線性
+關注
關注
0文章
198瀏覽量
25151 -
Transformer
+關注
關注
0文章
143瀏覽量
6007
原文標題:降低Transformer復雜度O(N^2)的方法匯總
文章出處:【微信號:vision263com,微信公眾號:新機器視覺】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
時間復雜度為 O(n^2) 的排序算法

如何降低LMS算法的計算復雜度,加快程序在DSP上運行的速度,實現DSP?
時間復雜度是指什么
各種排序算法的時間空間復雜度、穩定性
降低高條件數信道下的球形譯碼算法復雜度的方法
圖像復雜度對信息隱藏性能影響分析
Transformer的復雜度和高效設計及Transformer的應用
如何求遞歸算法的時間復雜度
如何計算時間復雜度




 降低Transformer復雜度O(N^2)的方法匯總
降低Transformer復雜度O(N^2)的方法匯總











評論