1 短時(shí)傅里葉變換STFT原理介紹
1.1 傅里葉變換的本質(zhì)
傅里葉變換的基本思想:
- 將信號(hào)分解成一系列不同頻率的連續(xù)正弦波的疊加;
- 或者說(shuō),將信號(hào)從時(shí)間域轉(zhuǎn)換到頻率域。
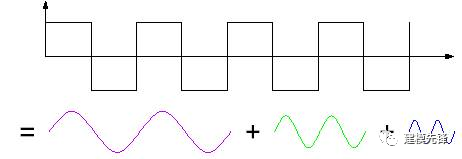
由于傅里葉變換是對(duì)整個(gè)信號(hào)進(jìn)行變換,將整個(gè)信號(hào)從時(shí)域轉(zhuǎn)換到頻域,得到一個(gè)整體的頻譜;丟掉了時(shí)間信息,無(wú)法根據(jù)傅立葉變換的結(jié)果判斷一個(gè)特定信號(hào)在什么時(shí)候發(fā)生;所以傅里葉變換缺乏時(shí)頻分析能力、多分辨率分析能力,難以分析非平穩(wěn)信號(hào)。
1.2 STFT概述
短時(shí)傅里葉變換(Short-Time Fourier Transform,STFT)是一種將信號(hào)分解為時(shí)域和頻域信息的時(shí)頻分析方法。它通過(guò)將信號(hào)分成短時(shí)段,并在每個(gè)短時(shí)段上應(yīng)用傅里葉變換來(lái)捕捉信號(hào)的瞬時(shí)頻率。即采用中心位于時(shí)間α的時(shí)間窗g(t-α)在時(shí)域信號(hào)上滑動(dòng),在時(shí)間窗g(t-α)限定的范圍內(nèi)進(jìn)行傅里葉變換,這樣就使短時(shí)傅里葉變換具有了時(shí)間和頻率的局部化能力,兼顧了時(shí)間和頻率的分析[1]。
- 使用窄窗,時(shí)間分辨率提高而頻率分辨率降低;
- 使用寬窗,頻率分辨率提高而時(shí)間分辨率降低。
比如用利用高斯窗STFT對(duì)非平穩(wěn)信號(hào)進(jìn)行分析:
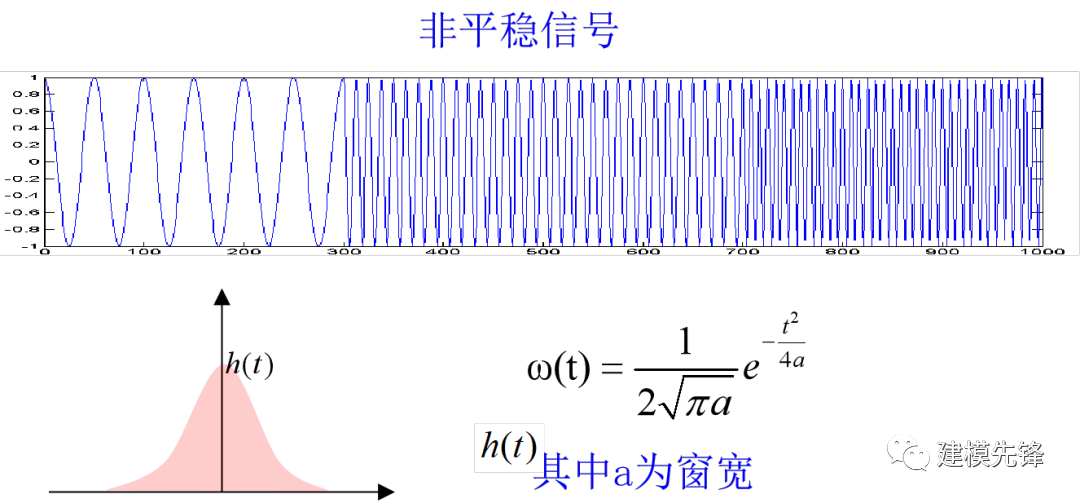
1.3 STFT的原理和過(guò)程
1.3.1 時(shí)間分割
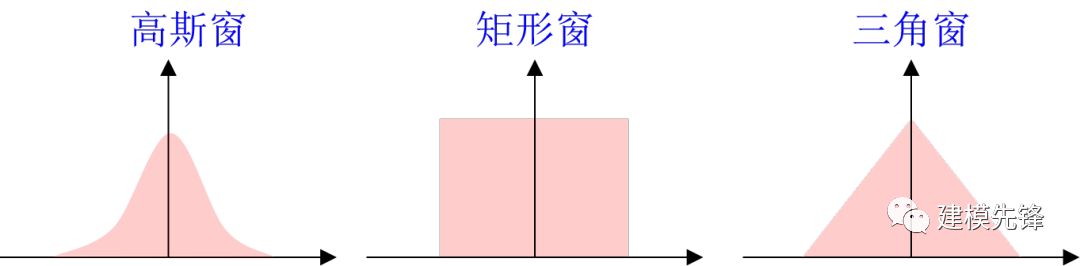
在短時(shí)傅里葉變換(STFT)中,首先將信號(hào)分割成短時(shí)段。這個(gè)過(guò)程通常通過(guò)使用窗口函數(shù)來(lái)實(shí)現(xiàn),窗口函數(shù)是一個(gè)在有限時(shí)間內(nèi)非零,而在其他時(shí)間上為零的函數(shù)。常見(jiàn)的窗口函數(shù)有矩形窗、漢明窗、漢寧窗等。通過(guò)將窗口函數(shù)應(yīng)用于信號(hào),可以將信號(hào)分成許多短時(shí)段。
1.3.2 傅里葉變換
對(duì)于每個(gè)短時(shí)段,都會(huì)進(jìn)行傅里葉變換。傅里葉變換是一種將信號(hào)從時(shí)域(時(shí)間域)轉(zhuǎn)換為頻域(頻率域)的方法。在這個(gè)上下文中,它用于分析每個(gè)短時(shí)段內(nèi)信號(hào)的頻率成分。傅里葉變換將信號(hào)表示為不同頻率的正弦和余弦函數(shù)的組合。
1.3.3 時(shí)頻圖:
將每個(gè)短時(shí)段的傅里葉變換結(jié)果排列成一個(gè)矩陣,構(gòu)成了時(shí)頻圖。時(shí)頻圖的橫軸表示時(shí)間,縱軸表示頻率,而每個(gè)點(diǎn)的強(qiáng)度表示對(duì)應(yīng)頻率在對(duì)應(yīng)時(shí)刻的幅度。時(shí)頻圖提供了一種直觀的方式來(lái)觀察信號(hào)在時(shí)間和頻率上的變化。
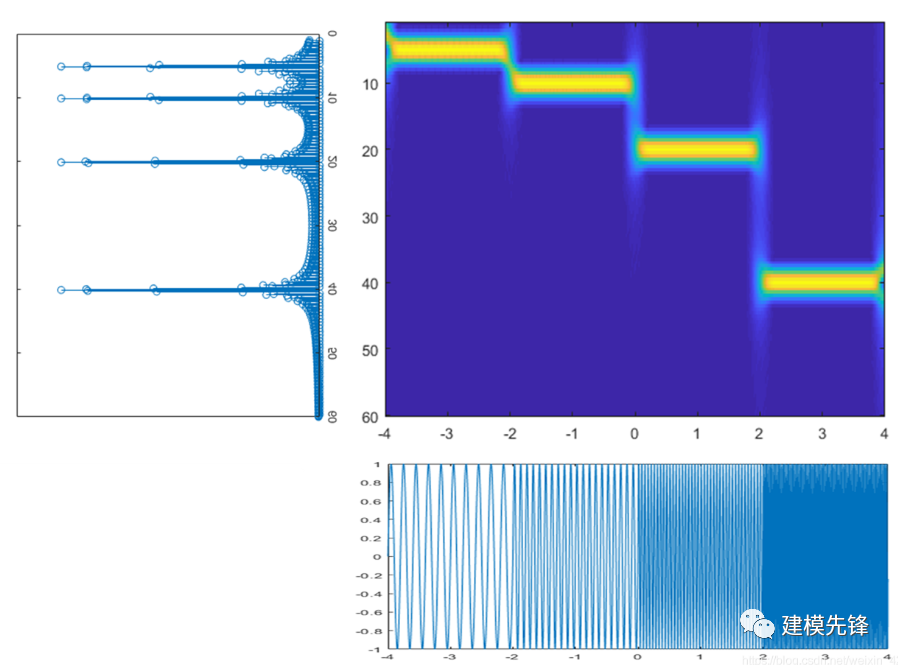
1.4 公式表示
STFT的數(shù)學(xué)表達(dá)式如下:
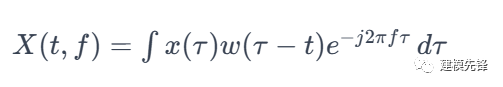
其中,

2 基于Python的STFT實(shí)現(xiàn)與參數(shù)對(duì)比
在 Python 中,使用 scipy 庫(kù)來(lái)實(shí)現(xiàn)短時(shí)傅里葉變換(STFT)
2.1 代碼示例
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import stft
# 生成三個(gè)不同頻率成分的信號(hào)
fs = 1000 # 采樣率
t = np.linspace(0, 1, fs, endpoint=False) # 時(shí)間
# 第一個(gè)頻率成分
signal1 = np.sin(2 * np.pi * 50 * t)
# 第二個(gè)頻率成分
signal2 = np.sin(2 * np.pi * 120 * t)
# 第三個(gè)頻率成分
signal3 = np.sin(2 * np.pi * 300 * t)
# 合并三個(gè)信號(hào)
signal = np.concatenate((signal1, signal2, signal3))
# 進(jìn)行短時(shí)傅里葉變換
f, t, spectrum = stft(signal, fs, nperseg=100, noverlap=50)
# 繪制時(shí)頻圖
plt.pcolormesh(t, f, np.abs(spectrum), shading='gouraud')
plt.title('STFT Magnitude')
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.show()
參數(shù)解釋
- nperseg:表示每個(gè)段的長(zhǎng)度,即窗口大小
- noverlap:表示相鄰段的重疊部分
- f:是頻率數(shù)組,表示頻譜的頻率分量
- t:是時(shí)間數(shù)組,表示每個(gè)時(shí)間段的起始時(shí)間
- spectrum:是頻譜矩陣,spectrum[f, t] 表示在頻率 f 處于時(shí)間 t 時(shí)的頻譜強(qiáng)度
可以使用 np.abs(spectrum) 獲取頻譜的幅度,表示在不同頻率和時(shí)間上的信號(hào)強(qiáng)度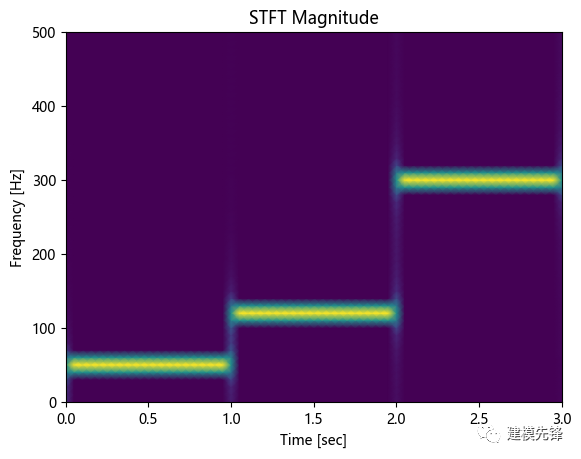
2.2 參數(shù)選擇和對(duì)比
2.2.1 nperseg(窗口長(zhǎng)度):
- nperseg 定義了每個(gè)時(shí)間段內(nèi)的信號(hào)長(zhǎng)度,也就是說(shuō),它規(guī)定了窗口的大小。
- **較小的 **nperseg 可以提供更高的時(shí)間分辨率,因?yàn)榇翱诟蹋梢圆蹲降叫盘?hào)的更快變化。但頻率分辨率較差。
- 較大的 nperseg 提供更高的頻率分辨率,但可能失去對(duì)信號(hào)快速變化的捕捉。
- 選擇適當(dāng)?shù)拇翱陂L(zhǎng)度要根據(jù)信號(hào)特性,如頻率變化的速率和信號(hào)長(zhǎng)度等。
2.2.2 noverlap(重疊長(zhǎng)度):
- noverlap 定義了相鄰時(shí)間段之間的重疊部分。
- **較大的 **noverlap 可以提高時(shí)間分辨率,因?yàn)橄噜彆r(shí)間段之間有更多的共享信息。但可能導(dǎo)致頻譜圖中的泄漏(leakage)。
- **較小的 **noverlap 可以提高頻率分辨率,減少泄漏,但時(shí)間分辨率可能下降。
2.2.3 選擇策略:
參數(shù)的選擇需要考慮到對(duì)信號(hào)分析的具體需求,平衡時(shí)間和頻率分辨率,嘗試不同的 nperseg 和 noverlap 值,觀察結(jié)果的變化。
- 對(duì)于 nperseg,選擇較小的值可能需要根據(jù)信號(hào)的特定頻率內(nèi)容進(jìn)行調(diào)整。確保窗口足夠短,以捕捉到頻率變化。
- 對(duì)于 noverlap,通常選擇 50% 的重疊是一個(gè)常見(jiàn)的起點(diǎn)
2.3 凱斯西儲(chǔ)大學(xué)軸承數(shù)據(jù)的加載
選擇正常信號(hào)和 0.021英寸內(nèi)圈、滾珠、外圈故障信號(hào)數(shù)據(jù)來(lái)做對(duì)比
第一步,導(dǎo)入包,讀取數(shù)據(jù)
import numpy as np
from scipy.io import loadmat
import numpy as np
from scipy.signal import stft
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc("font", family='Microsoft YaHei')
# 讀取MAT文件
data1 = loadmat('0_0.mat') # 正常信號(hào)
data2 = loadmat('21_1.mat') # 0.021英寸 內(nèi)圈
data3 = loadmat('21_2.mat') # 0.021英寸 滾珠
data4 = loadmat('21_3.mat') # 0.021英寸 外圈
# 注意,讀取出來(lái)的data是字典格式,可以通過(guò)函數(shù)type(data)查看。
第二步,數(shù)據(jù)集中統(tǒng)一讀取 驅(qū)動(dòng)端加速度數(shù)據(jù),取一個(gè)長(zhǎng)度為1024的信號(hào)進(jìn)行后續(xù)觀察和實(shí)驗(yàn)
# DE - drive end accelerometer data 驅(qū)動(dòng)端加速度數(shù)據(jù)
data_list1 = data1['X097_DE_time'].reshape(-1)
data_list2 = data2['X209_DE_time'].reshape(-1)
data_list3 = data3['X222_DE_time'].reshape(-1)
data_list4 = data4['X234_DE_time'].reshape(-1)
# 劃窗取值(大多數(shù)窗口大小為1024)
data_list1 = data_list1[0:1024]
data_list2 = data_list2[0:1024]
data_list3 = data_list3[0:1024]
data_list4 = data_list4[0:1024]
第三步,進(jìn)行數(shù)據(jù)可視化
plt.figure(figsize=(20,10))
plt.subplot(2,2,1)
plt.plot(data_list1)
plt.title('正常')
plt.subplot(2,2,2)
plt.plot(data_list2)
plt.title('內(nèi)圈')
plt.subplot(2,2,3)
plt.plot(data_list3)
plt.title('滾珠')
plt.subplot(2,2,4)
plt.plot(data_list4)
plt.title('外圈')
plt.show()
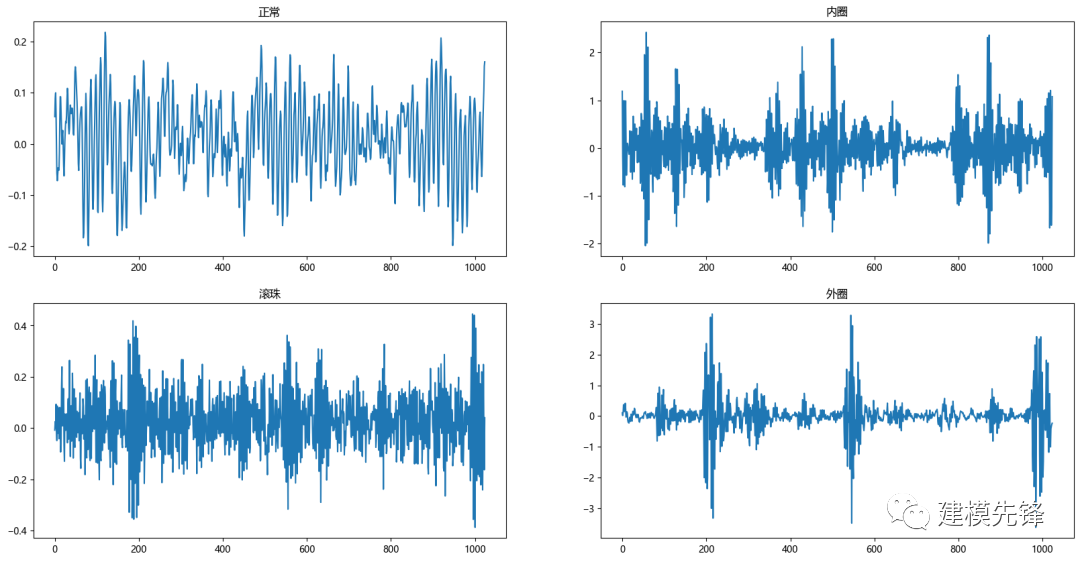
2.4 STFT與參數(shù)選擇
2.4.1 基于重疊比例為0.5,選擇內(nèi)圈數(shù)據(jù)比較 STFT 的不同尺度:16、32 、64、128
from scipy.signal import stft
# 設(shè)置STFT參數(shù)
window_size = 32 # 窗口大小
overlap = 0.5 # 重疊比例
# 計(jì)算重疊的樣本數(shù)
overlap_samples = int(window_size * overlap)
frequencies1, times1, magnitude1 = stft(data_list2, nperseg=window_size, noverlap=overlap_samples)
# 設(shè)置STFT參數(shù)
window_size = 64 # 窗口大小
overlap = 0.5 # 重疊比例
# 計(jì)算重疊的樣本數(shù)
overlap_samples = int(window_size * overlap)
frequencies2, times2, magnitude2 = stft(data_list2, nperseg=window_size, noverlap=overlap_samples)
# 設(shè)置STFT參數(shù)
window_size = 128 # 窗口大小
overlap = 0.5 # 重疊比例
# 計(jì)算重疊的樣本數(shù)
overlap_samples = int(window_size * overlap)
frequencies3, times3, magnitude3 = stft(data_list2, nperseg=window_size, noverlap=overlap_samples)
# 設(shè)置STFT參數(shù)
window_size = 256 # 窗口大小
overlap = 0.5 # 重疊比例
# 計(jì)算重疊的樣本數(shù)
overlap_samples = int(window_size * overlap)
frequencies4, times4, magnitude4 = stft(data_list2, nperseg=window_size, noverlap=overlap_samples
數(shù)據(jù)可視化
plt.figure(figsize=(20,10), dpi=100)
plt.subplot(2,2,1)
plt.pcolormesh(times1, frequencies1, np.abs(magnitude1), shading='gouraud')
plt.title('尺度 16-內(nèi)圈')
plt.subplot(2,2,2)
plt.pcolormesh(times2, frequencies2, np.abs(magnitude2), shading='gouraud')
plt.title('尺度 32-內(nèi)圈')
plt.subplot(2,2,3)
plt.pcolormesh(times3, frequencies3, np.abs(magnitude3), shading='gouraud')
plt.title('尺度 64-內(nèi)圈')
plt.subplot(2,2,4)
plt.pcolormesh(times4, frequencies4, np.abs(magnitude4), shading='gouraud')
plt.title('尺度 128-內(nèi)圈')
plt.show()
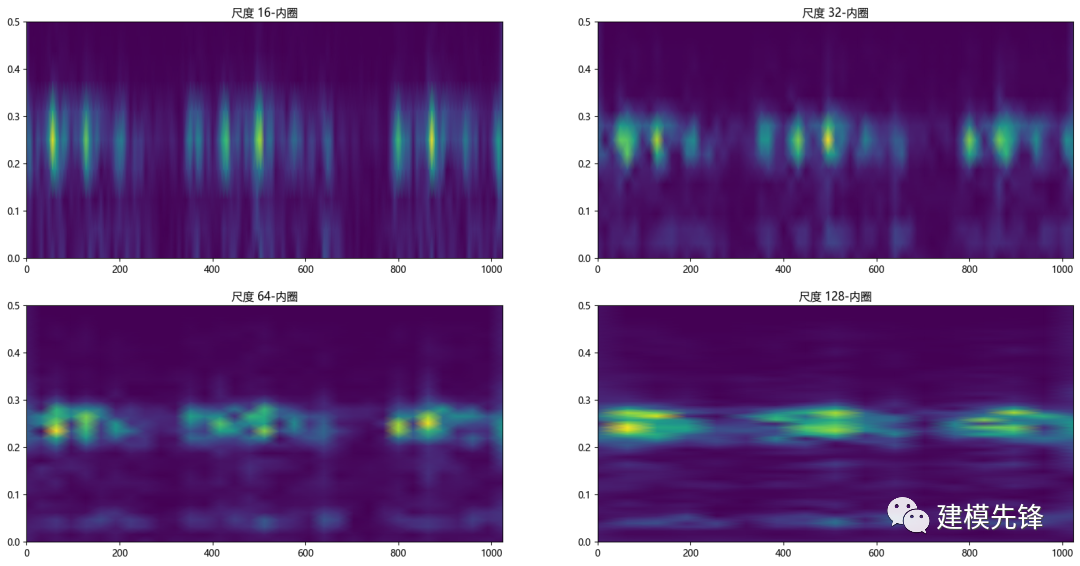
對(duì)比不同尺度的變化,大尺度有著較高的頻率分辨率,小的尺度有著較高的時(shí)間分辨率,要權(quán)衡故障的分類辨識(shí)度,需要進(jìn)一步做對(duì)比。
2.4.1 根據(jù)正常數(shù)據(jù)和三種故障數(shù)據(jù),對(duì)比不同尺度的辨識(shí)度
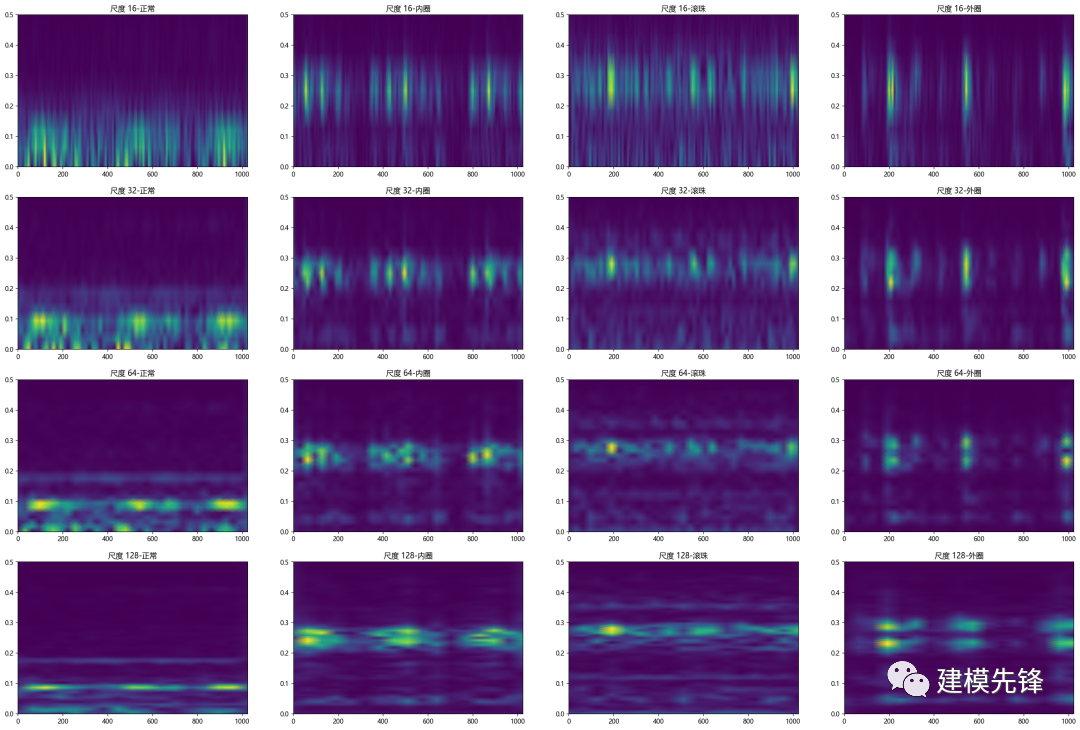
綜合考慮頻率分辨率和時(shí)間分辨率,選擇尺度為32。
3 基于時(shí)頻圖像的軸承故障診斷分類
下面以短時(shí)傅里葉變換(Short Time Fourier Transform,STFT)作為軸承故障數(shù)據(jù)的處理方法進(jìn)行講解:
數(shù)據(jù)介紹,凱斯西儲(chǔ)大學(xué)(CWRU)軸承數(shù)據(jù)10分類數(shù)據(jù)集如圖所示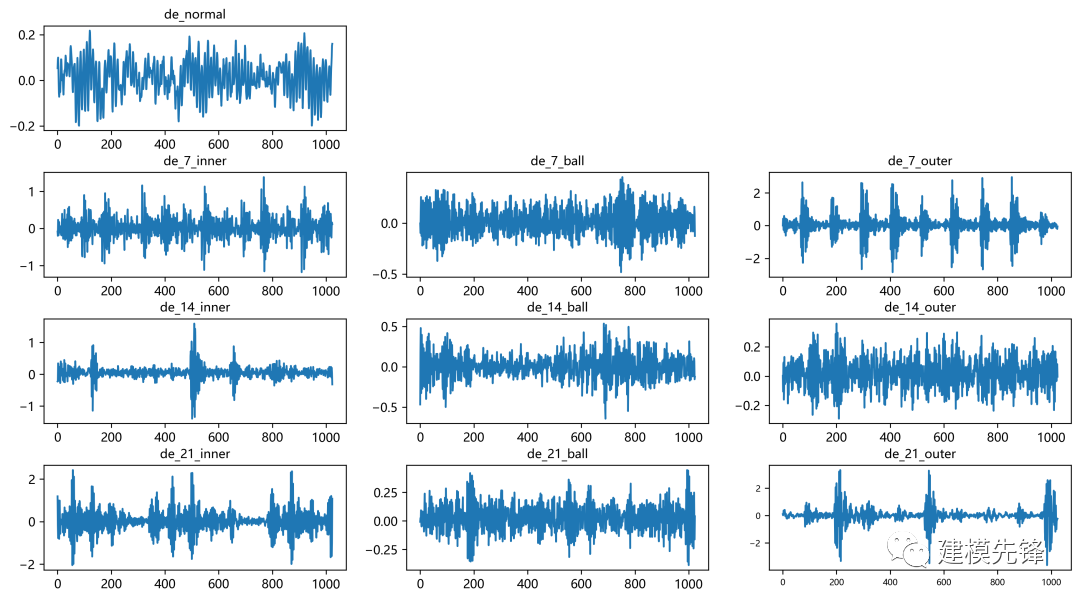
train_set、val_set、test_set 均為按照7:2:1劃分訓(xùn)練集、驗(yàn)證集、測(cè)試集,最后保存數(shù)據(jù)
3.1 生成時(shí)頻圖像數(shù)據(jù)集
如圖所示為生成的時(shí)頻圖像數(shù)據(jù)集

3.2 定義數(shù)據(jù)加載器和VGG網(wǎng)絡(luò)模型
制作數(shù)據(jù)標(biāo)簽,保存數(shù)據(jù)
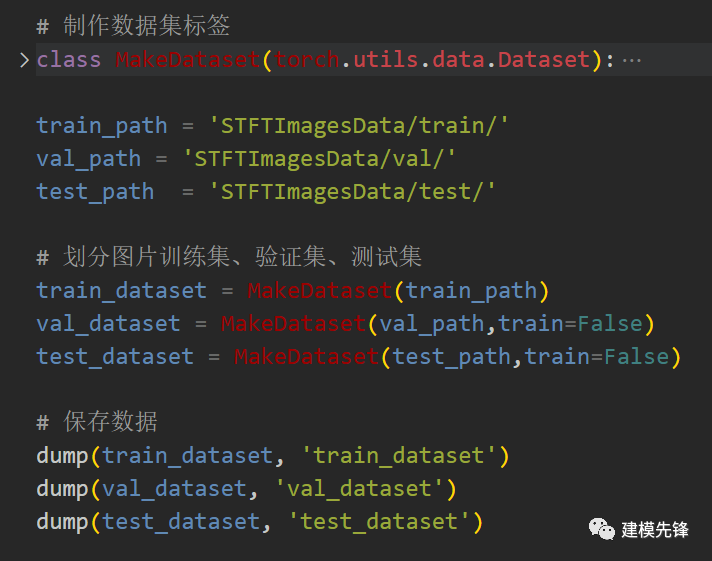
定義VGG網(wǎng)絡(luò)模型
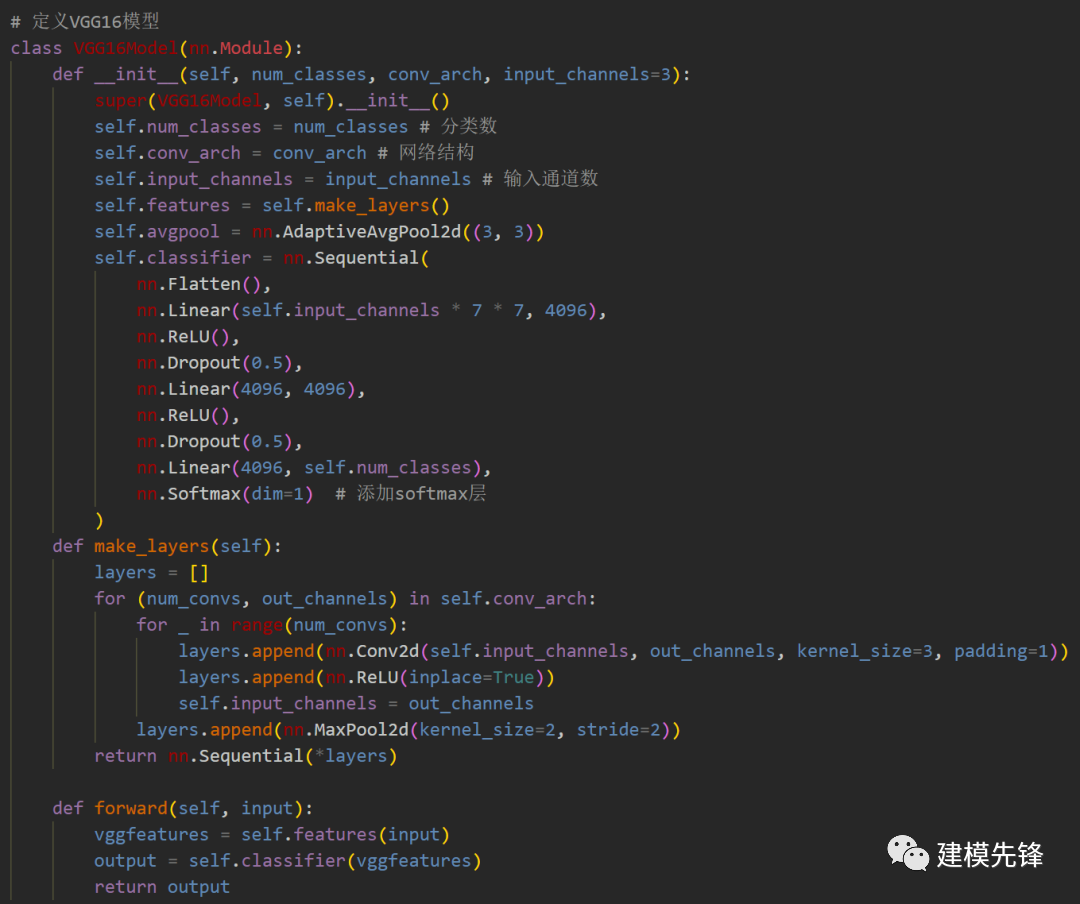
3.3 設(shè)置參數(shù),訓(xùn)練模型
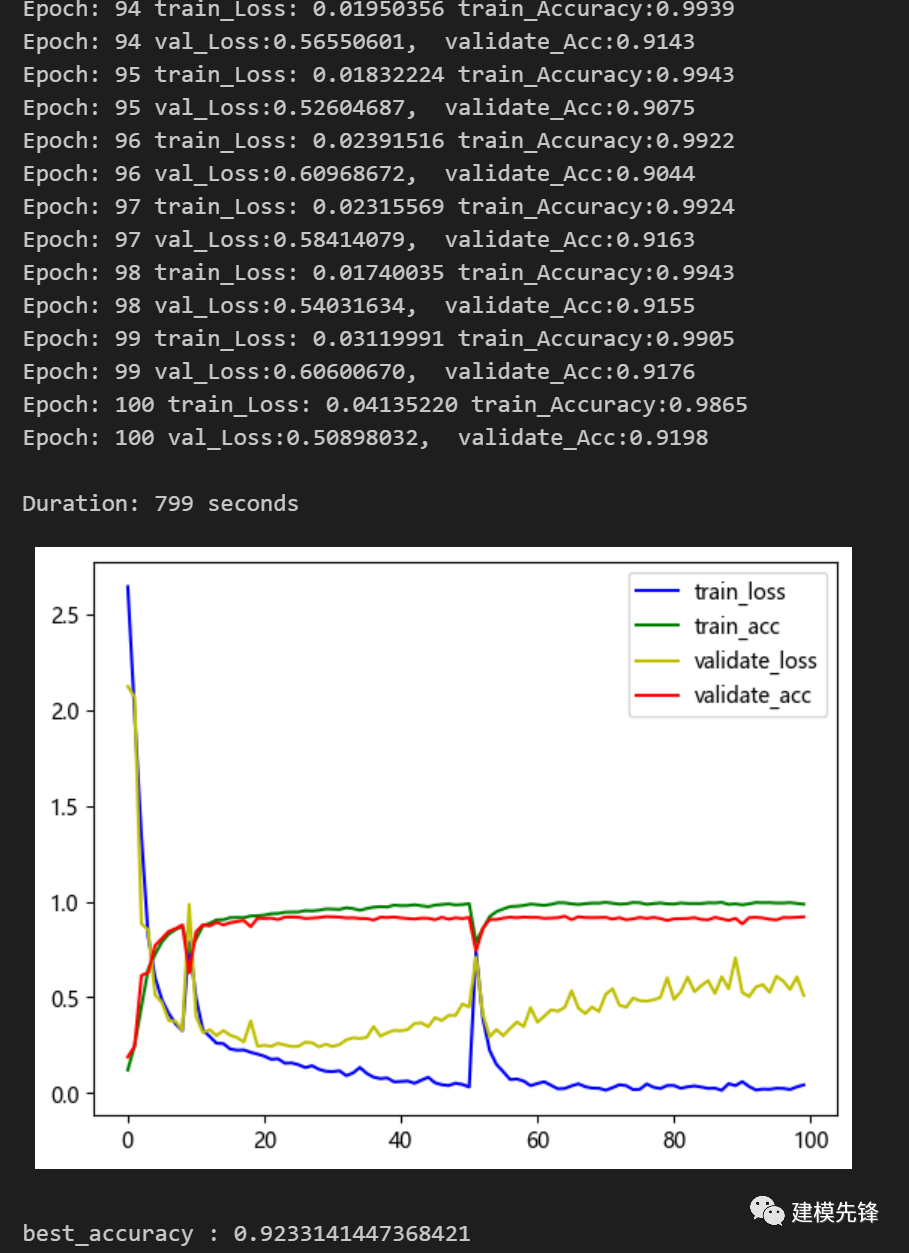
100個(gè)epoch,準(zhǔn)確率將近92%,繼續(xù)調(diào)參可以進(jìn)一步提高分類準(zhǔn)確率.
-
正弦波
+關(guān)注
關(guān)注
11文章
647瀏覽量
55514 -
python
+關(guān)注
關(guān)注
56文章
4801瀏覽量
84861 -
傅里葉變換
+關(guān)注
關(guān)注
6文章
442瀏覽量
42651 -
STFT
+關(guān)注
關(guān)注
0文章
11瀏覽量
9281
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
短時(shí)傅里葉變換STFT原理詳解

基于labview的軸承故障診斷與健康監(jiān)測(cè)
DSP的滾動(dòng)軸承實(shí)時(shí)故障診斷系統(tǒng)設(shè)
船舶感應(yīng)電機(jī)軸承故障診斷方法的幾點(diǎn)研究
【轉(zhuǎn)】電力電子電路故障診斷方法
基于DSP+MCU的列車滾動(dòng)軸承故障診斷系統(tǒng)研究
電機(jī)軸承故障診斷與分析
基于小波變換的故障診斷信號(hào)非平穩(wěn)性分析
滾動(dòng)軸承故障診斷的實(shí)用技巧
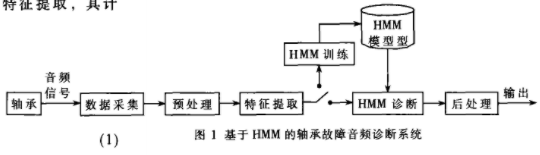
基于HMM的音頻故障診斷平臺(tái)實(shí)現(xiàn)軸承建模與診斷實(shí)驗(yàn)
短時(shí)傅里葉變換特點(diǎn) 短時(shí)傅里葉變換的意義
短時(shí)傅里葉變換和小波變換差別
故障診斷與python的實(shí)驗(yàn)仿真方法





 Python軸承故障診斷—短時(shí)傅里葉變換STFT簡(jiǎn)析
Python軸承故障診斷—短時(shí)傅里葉變換STFT簡(jiǎn)析










評(píng)論