隨著國家大力發(fā)展數(shù)字經(jīng)濟,算力的提升和普惠變得越來越重要。在數(shù)字化時代,算力已成為推動科技發(fā)展和創(chuàng)新的關(guān)鍵要素。它不僅僅是衡量計算機處理速度的標準,還涉及計算機系統(tǒng)或設(shè)備執(zhí)行計算任務(wù)的能力、數(shù)據(jù)處理能力以及解決復(fù)雜計算問題的能力。那么算力到底是什么呢?
簡單了解算力
算力(Computational Power)在計算機科學和計算領(lǐng)域中是一個重要概念,它指的是計算機系統(tǒng)或設(shè)備執(zhí)行數(shù)值計算和處理任務(wù)的能力。提升算力意味著可以更快地執(zhí)行復(fù)雜的計算任務(wù),從而提高計算的效率和性能。簡單來說,算力決定了計算機處理信息的速度和效率,直接影響我們使用電子設(shè)備的體驗,例如網(wǎng)頁加載速度和游戲流暢度等。
在數(shù)字經(jīng)濟時代,算力是新的生產(chǎn)力,為加強數(shù)字政府建設(shè)、激活數(shù)據(jù)要素潛能以及實現(xiàn)各行各業(yè)的數(shù)字化轉(zhuǎn)型提供了動力。據(jù)中國信息通信研究所的測算,每投入1元的算力,可以帶動3至4元的經(jīng)濟產(chǎn)出。算力的提升對經(jīng)濟具有巨大的影響力。根據(jù)統(tǒng)計數(shù)據(jù)顯示,每提高一個算力指數(shù)點,可以帶動數(shù)字經(jīng)濟增長 0.36% 和 GDP 增長 0.17%。
那算力大小具體是如何衡量的呢?這里就必須提及浮點運算,接下來我們來了解下浮點運算這個概念。
什么是浮點運算
算力最基本的計量單位是 FLOPS,英文 Floating-point Operations Per Second,即每秒執(zhí)行的浮點運算次數(shù)。浮點運算其實就是帶小數(shù)的加減乘除運算。
舉個例子:1.1+2.2 就是典型的浮點運算,估計你已經(jīng)心算出結(jié)果是 3.3 了。不過對計算機來說,這個問題并不簡單。我們知道,計算機是以 0 和 1 構(gòu)成的二進制數(shù)字進行運算的,比如在基礎(chǔ)的二進制里,1 就是 1,2 就變成了 “10”,3 是 “11”,這也帶來一個問題:計算機能夠處理的數(shù)字只有整數(shù)。
其實,0.1 可以看成是1除以10的結(jié)果,我們想讓計算機計算一個帶小數(shù)點的數(shù)字,只要告訴 CPU 這是一個被 1 后面加了多少個 0 整除的整數(shù)就行了。這樣一來,計算機在處理小數(shù)點的時候,就多了好幾個運算步驟。浮點運算的速度也就成了衡量計算機性能的標準。
算力的計量單位,除了 FLOPS,從小到大還有:
KFLOPS(每秒1000次浮點運算,10^3)
MFLOPS(每秒1百萬次,10^6)
GFLOPS(每秒10億次,10^9)
TFLOPS(每秒1萬億次,10^12)
PFLOPS(每秒1000萬億次,10^15)
EFLOPS(每秒100億億次,10^18)
浮點數(shù)
浮點數(shù)的浮點就是指它的小數(shù)點的位置是可以是漂浮不定的。這怎么理解呢?其實,浮點數(shù)是采用科學計數(shù)法的方式來表示的,例如十進制小數(shù) 1.234,用科學計數(shù)法表示,可以有多種方式:
1.234 = 1.234 * 10^0 1.234 = 12.34 * 10^-1 1.234 = 123.4 * 10^-2 ...
用這種科學計數(shù)法的方式表示小數(shù)時,小數(shù)點的位置就變得漂浮不定了。使用同樣的規(guī)則,對于二進制數(shù),我們也可以用科學計數(shù)法表示,也就是說把基數(shù) 10 換成 2 即可。那浮點數(shù)如何表示數(shù)字?其實浮點數(shù)是采用科學計數(shù)法來表示一個數(shù)字的,它的格式可以寫成這樣:
V = (-1)^S * M * R^E
其中各個變量的含義如下:
S:符號位,取值 0 或 1,決定一個數(shù)字的符號,0 表示正,1 表示負
M:尾數(shù),用小數(shù)表示,例如前面所看到的 1.234 * 10^0,1.234 就是尾數(shù)
R:基數(shù),表示十進制數(shù) R 就是 10,表示二進制數(shù) R 就是 2
E:指數(shù),用整數(shù)表示,例如前面看到的 10^-1,-1 即是指數(shù)
如果我們要在計算機中,用浮點數(shù)表示一個數(shù)字,只需要確認這幾個變量即可。
舉個例子:將十進制數(shù) 0.125 轉(zhuǎn)換為浮點數(shù),我們可以使用二進制浮點數(shù)表示。
符號位(S):由于數(shù)字為正數(shù),所以 S = 0。
尾數(shù)(M):將小數(shù)部分轉(zhuǎn)換為二進制。0.125 的二進制表示為 0.001。
基數(shù)(R):對于二進制數(shù),R = 2。
指數(shù)(E):確定指數(shù)的值。將 0.125 轉(zhuǎn)換為科學計數(shù)法形式可得 0.125 = 1.0 * 2^-3。因此,指數(shù) E = -3。
代入公式:V = (-1)^S * M * R^E
將以上值代入公式可得:
V = (-1)^0 * 0.001 * 2^-3 = 0.001 * 0.125
運算結(jié)果為 0.000001。因此十進制數(shù) 0.125 在二進制浮點數(shù)表示下為 0.000001。
計算機中使用有限的連續(xù)字節(jié)來保存浮點數(shù),而 IEEE 754標準定義了三種常見的浮點數(shù)格式:單精度、雙精度和擴展雙精度,它們適用于不同的計算需求。一般來說,單精度適合一般計算,雙精度適合科學計算,擴展雙精度適合高精度計算。一個遵循 IEEE 754標準的系統(tǒng)必須支持單精度類型(強制類型),最好也支持雙精度類型(推薦類型),而擴展雙精度類型則是可選的。
單精度浮點數(shù)(FP32)
單精度浮點數(shù)格式(英語:single-precision floating-point format)是一種數(shù)據(jù)類型,在計算機存儲器中占用 4 個字節(jié)(32 bits),利用 “浮點”(浮動小數(shù)點)的方法,可以表示一個范圍很大的數(shù)值。在 IEEE 754-2008 的定義中,32-bit base 2 格式被正式稱為 binary32 格式。這種格式在 IEEE 754-1985 被定義為 single,即單精度。需要注意的是,在更早的一些計算機系統(tǒng)中,也存在著其他 4 字節(jié)的浮點數(shù)格式。
第 1 位表示正負,中間 8 位表示指數(shù),后 23 位儲存有效數(shù)位(有效數(shù)位是 24 位)。第一位的正負號 0 代表正,1 代表負。中間八位共可表示 2^8 = 256 個數(shù),指數(shù)可以是二補碼;或 0 到 255,0 到 126 代表 -127 到 -1,127 代表零,128-255 代表 1-128。有效數(shù)位最左手邊的 1 并不會儲存,因為它一定存在(二進制的第一個有效數(shù)字必定是1)。換言之,有效數(shù)位是 24 位,實際儲存 23 位。
舉個例子:要將十進制數(shù) 0.125 轉(zhuǎn)換為單精度浮點數(shù)(32 位)。
遵循 IEEE 754 標準的表示方法,可以按照以下步驟進行轉(zhuǎn)換:
符號位(Sign):由于數(shù)字為正數(shù),所以符號位為 0。
尾數(shù)(Fraction):將小數(shù)部分轉(zhuǎn)換為二進制。0.125 的二進制表示為 0.001。
指數(shù)(Exponent):指數(shù)的偏移量為 127。由于 0.125 可以表示為 1.0 × 2^(-3),指數(shù)為 -3。加上偏移量后,實際指數(shù)為 -3 + 127 = 124。將 124 轉(zhuǎn)換為二進制得到 01111100。
組合位:將符號位、指數(shù)位和尾數(shù)位組合在一起,得到單精度浮點數(shù)的二進制表示。
最終的二進制表示為:0 01111100 00100000000000000000000
雙精度浮點數(shù)(FP64)
雙精度浮點數(shù)(Double Precision Floating Point),也稱為 FP64,是一種浮點數(shù)數(shù)據(jù)類型,用于在計算機中表示和進行高精度的浮點數(shù)運算。FP64 使用 64 個比特位(8 個字節(jié))來表示一個浮點數(shù),其中 1 位用于表示符號位(正負號),11 位用于表示指數(shù),52 位用于表示尾數(shù)。
雙精度浮點數(shù)的表示形式同樣采用科學計數(shù)法,即 ±M × 2^E,其中 M 為尾數(shù),E 為指數(shù)。通過使用更多的指數(shù)位和尾數(shù)位,F(xiàn)P64 相對于單精度浮點數(shù)能夠表示更廣范圍和更高精度的數(shù)值。
舉個例子:將十進制數(shù) 0.125 轉(zhuǎn)換為雙精度浮點數(shù)(64位)。
遵循 IEEE 754 標準的表示方法,可以按照以下步驟進行轉(zhuǎn)換:
符號位(Sign):由于數(shù)字為正數(shù),所以符號位為 0。
尾數(shù)(Fraction):將小數(shù)部分轉(zhuǎn)換為二進制。0.125 的二進制表示為 0.001。
指數(shù)(Exponent):指數(shù)的偏移量為 1023。由于 0.125 可以表示為 1.0 × 2^(-3),指數(shù)為 -3。加上偏移量后,實際指數(shù)為 -3 + 1023 = 1020。將 1020 轉(zhuǎn)換為二進制得到 01111111100。
組合位:將符號位、指數(shù)位和尾數(shù)位組合在一起,得到雙精度浮點數(shù)的二進制表示。
最終的二進制表示為:0 01111111100 0010000000000000000000000000000000000000000000000000
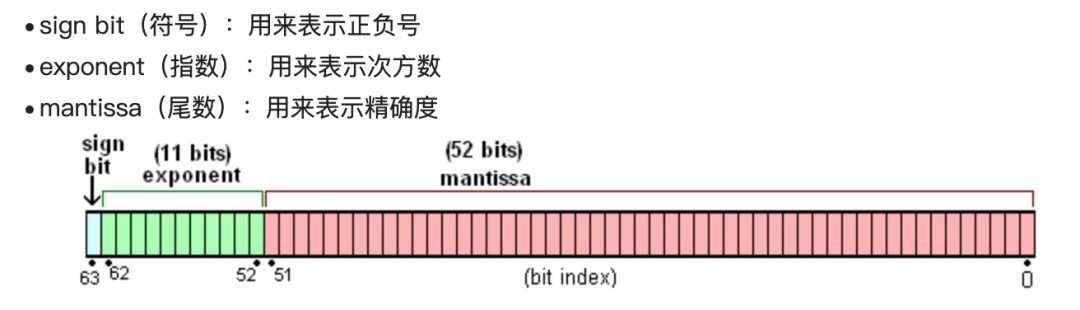
雙精度浮點數(shù)的取值范圍約為 ±4.9 × 10^-324 到 ±1.8 × 10^308,并提供大約 15 到 16 位有效數(shù)字的精度。相比于單精度浮點數(shù),雙精度浮點數(shù)能夠處理更大范圍的數(shù)值和提供更高的精度,適用于對精確性要求較高的計算任務(wù)。
雙精度浮點數(shù)常用于科學計算、工程應(yīng)用、金融分析和高性能計算等領(lǐng)域。它在這些領(lǐng)域中被廣泛用于處理實數(shù)數(shù)據(jù),如數(shù)值模擬、大規(guī)模計算、天文學、物理學和工程計算等。
然而,需要注意的是,雙精度浮點數(shù)的存儲空間和計算開銷相對于單精度浮點數(shù)更高。在某些情況下,如果對精度要求不高或者計算資源有限,可以考慮使用單精度浮點數(shù)進行計算,以提高計算效率和節(jié)省內(nèi)存消耗。
浮點數(shù)的舍入
由于浮點數(shù)計算過程中丟失了精度,浮點運算的性質(zhì)與數(shù)學運算有所不同。任何有效數(shù)上的運算結(jié)果,通常都存放在較長的寄存器中,當結(jié)果被放回浮點格式時,必須將多出來的比特丟棄。IEEE 標準列出 4 種不同的方法:
舍入到最接近:舍入到最接近,在一樣接近的情況下偶數(shù)優(yōu)先(Ties To Even,這是默認的舍入方式):會將結(jié)果舍入為最接近且可以表示的值,但是當存在兩個數(shù)一樣接近的時候,則取其中的偶數(shù)(在二進制中是以0結(jié)尾的)。
朝 +∞ 方向舍入:會將結(jié)果朝正無限大的方向舍入。
朝 -∞ 方向舍入:會將結(jié)果朝負無限大的方向舍入。
朝 0 方向舍入:會將結(jié)果朝 0 的方向舍入。
單、雙精度的應(yīng)用場景
單精度浮點數(shù)通常應(yīng)用在需要較高計算速度的場景,例如嵌入式系統(tǒng)和移動設(shè)備。在這些應(yīng)用中,對于一些實時性要求較高的任務(wù),如圖形渲染、音視頻處理等,單精度浮點數(shù)能夠提供足夠的精度,并且在存儲和計算上更加高效,能夠滿足實時性和資源限制的需求。此外,單精度浮點數(shù)也廣泛應(yīng)用于科學研究和工程領(lǐng)域中的數(shù)值計算,包括求解方程、模擬物理過程等。在這些領(lǐng)域中,單精度浮點數(shù)的精度已經(jīng)足夠滿足大部分的計算需求,同時可以提高計算速度和節(jié)省存儲空間。
雙精度浮點數(shù)主要應(yīng)用于需要更高精度的場景,如科學計算、工程計算、金融分析等。在這些領(lǐng)域中,對計算結(jié)果的精確性要求較高,需要更多的有效數(shù)字來表示和處理實數(shù)。雙精度浮點數(shù)能夠提供更高的精度和更大的表示范圍,能夠處理更復(fù)雜和精細的計算任務(wù)。在科學計算中,如天文學、數(shù)值模擬等領(lǐng)域,雙精度浮點數(shù)常常用于求解復(fù)雜的數(shù)學模型和算法,以獲得更準確的結(jié)果。在金融分析中,雙精度浮點數(shù)可以處理更大的數(shù)值范圍和更高的精度,確保計算結(jié)果的準確性和可靠性。
總之,選擇單精度還是雙精度浮點數(shù)應(yīng)根據(jù)具體應(yīng)用的需求來決定,需要權(quán)衡計算速度、精度要求和資源限制等因素。單精度浮點數(shù)適用于對計算速度要求較高且精度要求不是特別嚴格的場景,而雙精度浮點數(shù)適用于對精度要求更高的科學計算和工程領(lǐng)域。
CPU 和 GPU 的算力計算
目前服務(wù)器的算力主要包括 CPU 和 GPU 等不同芯片產(chǎn)生的算力。那具體到每臺服務(wù)器的算力,究竟如何計算呢?
CPU 的算力計算
我們以 CPU 的雙精度浮點運算能力(FP64)為例,單個 CPU 的算力,與 CPU 核心的個數(shù)、頻率、單時鐘周期浮點計算能力 3 個因素有關(guān)。
單 CPU 算力 = CPU 核數(shù) * 單核主頻 * 單周期浮點計算能力
以 Intel Cascade Lake 架構(gòu)的 Xeon Platinum 8280 為例,該 CPU 具有 28 個核心,主頻為 2.7GHz,并支持 AVX512 指令集。根據(jù)提供的信息,我們可以計算出該 CPU 的雙精度浮點運算能力(FP64)。
首先,計算單個 CPU 核心的單周期浮點計算能力:
單周期浮點計算能力 = 512bit * 2FMA * 2M/A / 64bit = 32 FLOPS/Cycle
然后,計算單個 CPU 核心的峰值浮點運算能力:
單個 CPU 核心的峰值浮點運算能力 = 單周期浮點計算能力 * 主頻 = 32 FLOPS/Cycle * 2.7 GHz
最后,計算整個 CPU 的峰值浮點運算能力:
單 CPU 算力 = CPU 核數(shù) * 單個 CPU 核心的峰值浮點運算能力 = 28 cores * 單個CPU核心的峰值浮點運算能力
根據(jù)提供的數(shù)據(jù),計算得到:
單個 CPU 核心的峰值浮點運算能力 = 32 FLOPS/Cycle * 2.7 GHz = 86.4 GFLOPS
單 CPU 算力 = 28 cores * 86.4 GFLOPS = 2.4192 TFLOPS
因此,以 Intel Cascade Lake 架構(gòu)的 Xeon Platinum 8280 為例,該 CPU 的理論峰值雙精度浮點性能為 2.4192 TFLOPS。
注:該計算是理論值,實際性能可能受到多種因素(如指令級并行性、內(nèi)存訪問延遲等)的影響。
GPU 的算力計算
GPU 的算力與上面的計算方法類似。單個 GPU 算力也是與核心個數(shù)、頻率、單時鐘周期能力 3 個因素有關(guān)。
以 NVIDIA Volta 架構(gòu)的 V100 為例,該 GPU 擁有 2560 個雙精度浮點核心(FP64 cores),主頻為 1.530GHz。
根據(jù)提供的信息,我們可以計算出該 GPU 的雙精度浮點運算能力(FP64)。
首先,計算單個 GPU 核心的單周期浮點計算能力:
單周期浮點計算能力 = 64bit * 1FMA * 2M/A / 64bit = 2 FLOPS/Cycle
然后,計算單個 GPU 核心的峰值浮點運算能力:
單個 GPU 核心的峰值浮點運算能力 = 單周期浮點計算能力 * 主頻 = 2 FLOPS/Cycle * 1.530 GHz
最后,計算整個 GPU 的峰值浮點運算能力:
單 GPU 算力 = GPU 核數(shù) * 單個 GPU 核心的峰值浮點運算能力 = 2560 cores * 單個 GPU 核心的峰值浮點運算能力
根據(jù)提供的數(shù)據(jù),計算得到:
單個 GPU 核心的峰值浮點運算能力 = 2 FLOPS/Cycle * 1.530 GHz = 3.060 GFLOPS
單 GPU 算力 = 2560 cores * 3.060 GFLOPS = 7833 GFLOPS = 7.833 TFLOPS
因此,以 NVIDIA Volta 架構(gòu)的 V100 為例,該 GPU 的理論峰值雙精度浮點性能為 7.833 TFLOPS。
注:該計算是理論值,實際性能可能受到多種因素(如內(nèi)存帶寬、功耗限制等)的影響。
聊了這么多,相信大家對 CPU、GPU 的算力計算和浮點運算都有了一定的了解,雖然看起來比較復(fù)雜,其實還是比較好理解的。大家也可以收藏下這篇內(nèi)容,以備不時之需。
審核編輯:劉清
-
存儲器
+關(guān)注
關(guān)注
38文章
7518瀏覽量
164076 -
二進制
+關(guān)注
關(guān)注
2文章
795瀏覽量
41701 -
計算機
+關(guān)注
關(guān)注
19文章
7523瀏覽量
88315 -
浮點運算
+關(guān)注
關(guān)注
0文章
19瀏覽量
11188
原文標題:深入了解浮點運算——CPU和GPU算力是如何計算的
文章出處:【微信號:OSC開源社區(qū),微信公眾號:OSC開源社區(qū)】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
請問AURIX TC3xx tricore架構(gòu)下浮點運算和將浮點數(shù)小數(shù)點去掉變成整數(shù)來計算哪種方式更加節(jié)省算力?
名單公布!【書籍評測活動NO.43】 算力芯片 | 高性能 CPU/GPU/NPU 微架構(gòu)分析
【「算力芯片 | 高性能 CPU/GPU/NPU 微架構(gòu)分析」閱讀體驗】--全書概覽
《算力芯片 高性能 CPU/GPU/NPU 微架構(gòu)分析》第1-4章閱讀心得——算力之巔:從基準測試到CPU微架構(gòu)的深度探索
【「算力芯片 | 高性能 CPU/GPU/NPU 微架構(gòu)分析」閱讀體驗】--了解算力芯片CPU
【「算力芯片 | 高性能 CPU/GPU/NPU 微架構(gòu)分析」閱讀體驗】--了解算力芯片GPU
數(shù)據(jù)、算法和算力其實現(xiàn)載體是什么
Xilinx Zynq7035算力指標
CPU 的浮點運算能力比 GPU 差,為什么不提高 CPU 的浮點運算能力呢
FPGA運算單元對高算力浮點應(yīng)用
GPU是顯卡嗎 cpu和gpu哪個算力強
算力服務(wù)器為什么選擇GPU

【一文看懂】大白話解釋“GPU與GPU算力”





 深入了解浮點運算—CPU和GPU算力是如何計算的?
深入了解浮點運算—CPU和GPU算力是如何計算的?











評論