上期我們講了槽內(nèi)線圈的感應(yīng)電勢，解答了用“Blv觀點”計算槽內(nèi)線圈感應(yīng)電勢的有關(guān)問題，明確了電機(jī)線圈中的感應(yīng)電勢大小與電樞開槽無關(guān)，“Blv觀點”不僅適用于計算光滑電樞表面的線圈感應(yīng)電勢，而且也適用于計算電樞開槽后槽內(nèi)線圈感應(yīng)電勢的計算，但用“Blv觀點”計算槽內(nèi)線圈的感應(yīng)電勢時，其中的B必須用光滑電樞時的氣隙磁密值代入。

與此問題類似，通電導(dǎo)體在磁場中會受到的電磁力的作用，電磁力的大小可用“BIL”計算。具體到電機(jī)中，如果電樞是光滑的，線圈位于光滑電樞表面，則用“BIL觀點”計算線圈導(dǎo)體的受力，進(jìn)而計算電磁轉(zhuǎn)矩是非常容易理解的；如果電樞開槽，線圈的導(dǎo)體位于槽內(nèi)，同樣存在著槽內(nèi)的磁密很小，“BIL觀點”還是否適用的問題。如果能用，其中的B又應(yīng)該用何值代入？另外同學(xué)們還經(jīng)常問到一個問題，就是槽內(nèi)線圈產(chǎn)生的電磁力是作用在槽內(nèi)的導(dǎo)體上還是作用在鐵芯上？本期就來回答這些問題！

1 磁介質(zhì)在磁場中受到的磁場力

將一塊磁介質(zhì)(簡稱“磁質(zhì)”)置于磁場中，就會受到磁場力的作用。在磁質(zhì)的某點附近取一體積微元dV，設(shè)該體積微元所受到的磁力為dF，則定義dF/dV為該點磁質(zhì)所受到的體積磁力密度，即f=dF/dV。也就是說，磁質(zhì)上某點的磁力密度就是該點附近單位體積的磁質(zhì)所受到的磁場力。根據(jù)相關(guān)電磁理論，磁質(zhì)在磁場中所受到的體積磁力密度為：

f=J×B-(1/2)H2?gradμ+f″ ⑴

需要說明的是，上式為不失一般性的磁力密度表達(dá)式，全面考慮到了各種情況：其中第一項是考慮了磁質(zhì)中包含傳導(dǎo)電流所受到的磁場力，即通電導(dǎo)體在磁場中受到的磁力，也就是人們常說的“洛倫茲力”，式中：J為該點處的傳導(dǎo)電流密度矢量；B為該點處的磁密矢量，該項表明通電導(dǎo)體在磁場中所受到的磁力密度為電流密度矢量與磁密矢量的叉乘，進(jìn)一步推導(dǎo)(略)可知，如果電流方向與磁場方向垂直，則該項磁力的大小就等于BIL，作用點在載流導(dǎo)體上，方向可用左手定則判定；第二項是考慮了磁質(zhì)中各點的磁導(dǎo)率分布可能不同，式中：gradμ為該點磁導(dǎo)率的梯度；H為該點的磁場強度，該項表明當(dāng)磁質(zhì)內(nèi)各點的磁導(dǎo)率分布不均勻時，就會因各向磁阻不均勻而產(chǎn)生的磁力，稱為麥克斯韋力，麥克斯韋力的大小與該處磁導(dǎo)率的梯度成正比，該項前面的負(fù)號“-”表示麥克斯韋力的方向為從μ值大處指向μ值小處；第三項 f″則表示磁質(zhì)在磁場中受到應(yīng)力后發(fā)生變形，于是各方向的μ值發(fā)生變化而引起的力，稱為磁致伸縮力，通常在磁質(zhì)內(nèi)部 f″會被材料局部的彈力相平衡，屬于內(nèi)力，只影響磁質(zhì)內(nèi)部的應(yīng)力分布，不影響整個磁質(zhì)所受到的總合力，加之在簡化的鐵磁物質(zhì)模型中，認(rèn)為磁質(zhì)變形時μ并不隨之而變化，因此通常在電機(jī)中將該項忽略不計。這樣在分析實際電機(jī)中的電磁力時，就只考慮前面兩項——洛倫茲力和麥克斯韋力，并還可根據(jù)電機(jī)磁路的具體情況，作相應(yīng)的簡化。

整塊磁質(zhì)所受到的磁場力：

F=?【V】f?dV⑵

式中：【V】為積分區(qū)域，即整個磁質(zhì)的體積。

2 磁場通過兩種不同磁介質(zhì)時交界面上的磁場力

對于⑴式中的第二項——麥克斯韋力，若一種磁質(zhì)內(nèi)部的μ為常數(shù)(處處相等)，則該磁質(zhì)內(nèi)部gradμ=0，這就意味著同一磁介質(zhì)內(nèi)部的麥克斯韋力為0，但如果磁路中存在兩種磁介質(zhì)，例如電機(jī)的磁路中就存在鐵心與空氣兩種磁介質(zhì)，由于鐵心與空氣的磁導(dǎo)率相差巨大，那么在鐵心與空氣的交界面上就存在巨大的法向磁導(dǎo)率梯度gradμ，因此在交界面上就會產(chǎn)生巨大的麥克斯韋力。因此在分析電機(jī)中的電磁力時，往往不考慮鐵心內(nèi)部的體積磁力密度，而只考慮兩種不同介質(zhì)交界面上的面積磁力密度，即磁應(yīng)力，為此⑵式可寫作：

F=?【V】f?dV=?【A】σ?da⑶

式中：【A】為積分區(qū)域，即為包圍體積【V】的閉合曲面；σ為磁應(yīng)力，即單位面積上的電磁力；da為曲面A上的面積微元。

根據(jù)麥克斯韋張量理論，經(jīng)過一系列復(fù)雜的推導(dǎo)(略)，得出兩種不同磁介質(zhì)交界面上的磁應(yīng)力：

σ=(1/2μ)(Bn2-Bt2)n+(1/μ)Bn?Bt?t=σn+σt ⑷

式中：Bn和Bt分別為交界面上法向和切向的磁密；n和t分別代表交界面上的單位法向矢量和單位切向矢量；σn和σt分別為交界面上磁應(yīng)力的法向分量和切向分量：

σn=(1/2μ)(Bn2-Bt2)

σt=(1/μ)Bn?Bt ⑸

3 鐵心和空氣交界面的磁場力

如圖1所示表示鐵心和空氣形成交界面A。設(shè)空氣為介質(zhì)1，μ1=μ0，空氣側(cè)的磁密為B1；鐵心為介質(zhì)2，μ2=μFe，鐵心側(cè)的磁密為B2；磁場為二維平行平面場。

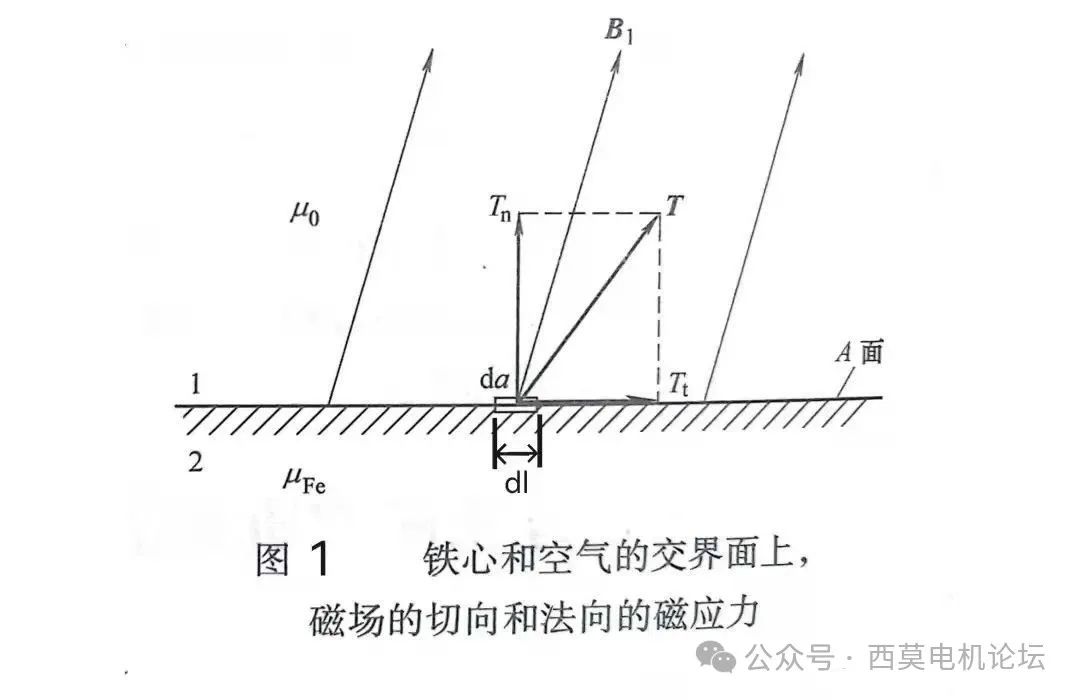
在交界面A上取一面積微元da，根據(jù)⑸式，空氣側(cè)磁應(yīng)力的切向分量σ1t和法向分量σ1n分別為：

σ1t=(1/μ0)B1n?B1t

σ1n=(1/2μ0)(B1n2-B1t2) ⑹

鐵心側(cè)磁應(yīng)力的切向分量和σ2t和法向分量σ2n分別為：

σ2t=(1/μFe)B2n?B2t

σ2n=(1/2μFe)(B2n2-B2t2) ⑺

于是作用在微元面積da上的合成切向磁應(yīng)力σt和法向磁應(yīng)力σn分別為：

σt=σ1t-σ2t=(1/μ0)B1n?B1t-(1/μFe)B2n?B2t

σn=σ1n-σ2n=(1/2μ0)(B1n2-B1t2)-(1/2μFe)(B2n2-B2t2) ⑻

若交界面上無電流層，則交界面上的邊界條件為：

B1n=B2n=Bn≈Bδ

H1t=H2t=Ht ⑼

式中：Bδ為氣隙磁密。

將⑼式代入⑻式得：

σt=0

σn=[(μFe-μ0)/(2μFe?μ0)]?(Bn2+μFe?μ0?Ht2) ⑽

由⑽式可見，當(dāng)交界面上無電流層時，交界面上僅有法向磁應(yīng)力，其方向為從鐵心指向空氣，切向應(yīng)力恒等于0。由于鐵心的磁導(dǎo)率遠(yuǎn)大于空氣的磁導(dǎo)率，即μFe＞＞μ0，故認(rèn)為磁力線進(jìn)入鐵心時，基本上垂直于鐵心表面，即Ht≈0，于是法向磁應(yīng)力可近似寫成：

σn≈Bn2/(2μ0)≈Bδ2/(2μ0) (11)

通常工程實踐中，都是用(11)式來計算法向磁應(yīng)力的。

4 線圈置于光滑電樞表面時的切向力

在實際電機(jī)中，如果把圖1中的鐵心側(cè)看作光滑的電樞鐵心；空氣側(cè)看作氣隙；把電樞繞組看作均勻分布在電樞鐵心與氣隙的交界面上，電樞繞組中的電流看作是均勻分布在交界面上沒有厚度的電流層。那么在電機(jī)空載時，交界面上沒有電流層，根據(jù)上述第3章的分析，分界面上的切向磁應(yīng)力和法向磁應(yīng)力即由(10)式?jīng)Q定，也就是說，光滑電樞的電機(jī)空載時切向磁應(yīng)力為0，只有法向磁應(yīng)力，法向磁應(yīng)力近似按(11)式計算。由于法向磁應(yīng)力不產(chǎn)生電磁轉(zhuǎn)矩，而產(chǎn)生電磁轉(zhuǎn)矩的切向磁應(yīng)力為0，因此空載時電磁轉(zhuǎn)矩為0。

負(fù)載時，電樞繞組中通有電流，即交界面上存在電流層有，設(shè)電樞圓周單位弧長上的電流為A′(即電機(jī)設(shè)計里的線負(fù)荷，為了區(qū)別于交界面A，這里用A′代表線負(fù)荷)：

A′=∑I/(2πR) (12)

式中：∑I為整個電樞圓周上的總電流，即各相電流的安導(dǎo)總和；R為電樞半徑。

接下來分析交界面上存在電流層時的邊界條件。首先看法向邊界條件，由于磁力線是不間斷的閉合曲線，因此在交界面上，鐵心和氣隙兩側(cè)的法向磁密相等，即交界面上的法向邊界條件仍然是B1n=B2n=Bn≈Bδ，交界面上的法向磁應(yīng)力仍然按(11)式計算。

再看切向邊界條件，圖1中將磁場強度H沿包圍面積微元da的閉合曲線周長積分就應(yīng)該等于da面積內(nèi)所包圍的電流，即：

H1t?dl+H2t?dl=A′?dl (13)

式中：H1t、H2t分別為分界面上空氣和鐵心側(cè)磁場強度的切向分量；dl為電樞圓周上的弧長微元。考慮到鐵心中的磁導(dǎo)率遠(yuǎn)大于空氣的磁導(dǎo)率，即μFe＞＞μ0，因此鐵心側(cè)的切向磁壓降可以忽略不計，認(rèn)為所有磁壓降全部降在氣隙側(cè)，即H2t?dl=0，H2t=0，于是有H1t=A′。因此交界面上的邊界條件為：

B1n=B2n=Bn≈Bδ

H1t=A′｝(14)

H2t=0

將上述法向和切向邊界條件代入⑻式的第一個公式，得負(fù)載時切向磁應(yīng)力為：

σt=(1/μ0)B1n?B1t

=B1n?H1t

=Bδ? A′ (15)

由(15) 式可見，電樞表面的切向磁應(yīng)力就是電機(jī)設(shè)計里所說的電磁負(fù)荷！

進(jìn)一步推導(dǎo)電機(jī)負(fù)載時總的切向力為：

Ft=σt?2πR?L

=Bδ?A′?2πR?L

=Bδ?∑I?L (16)

式中：L為鐵心有效長度。由(16)式可見，光滑電樞表面的電機(jī)，負(fù)載時的切向電磁力就是“BIL”。

小結(jié)一下：線圈置于光滑電樞表面時，空載切向磁應(yīng)力為0，法向磁應(yīng)力約為Bδ2/(2μ0)，電磁轉(zhuǎn)矩為0；負(fù)載時的法向磁應(yīng)力仍約為Bδ2/(2μ0)，切向磁應(yīng)力等于負(fù)載時的電磁負(fù)荷，切向電磁力可以用 “BIL觀點”來計算，切向電磁力的作用點是作用在線圈導(dǎo)體上，鐵心表面只受法向電磁力作用。

5 線圈置于電樞槽內(nèi)時的切向力

當(dāng)電樞開槽、導(dǎo)體嵌入槽內(nèi)以后，情況有了很大的變化。由于鐵心的磁導(dǎo)率遠(yuǎn)大于空氣的磁導(dǎo)率，槽內(nèi)磁通密度相對較低，因此載流導(dǎo)體放入槽內(nèi)后，導(dǎo)體上所受到的電磁力將急劇下降，此時切向磁場力和由此產(chǎn)生的電磁轉(zhuǎn)矩，大部份將集中在電樞齒壁上。下面用磁應(yīng)力來說明此問題。

如圖2a)表示空載時主極所產(chǎn)生的氣隙和槽內(nèi)磁場，圖b表示槽內(nèi)載流導(dǎo)體單獨作用(不考慮主極磁場)時，槽內(nèi)和氣隙中的磁場。設(shè)鐵心的磁導(dǎo)率μFe＝常值，把圖2a)和圖2b)兩個磁場疊加，可得負(fù)載時氣隙和槽內(nèi)的合成磁場，如圖2c)所示。

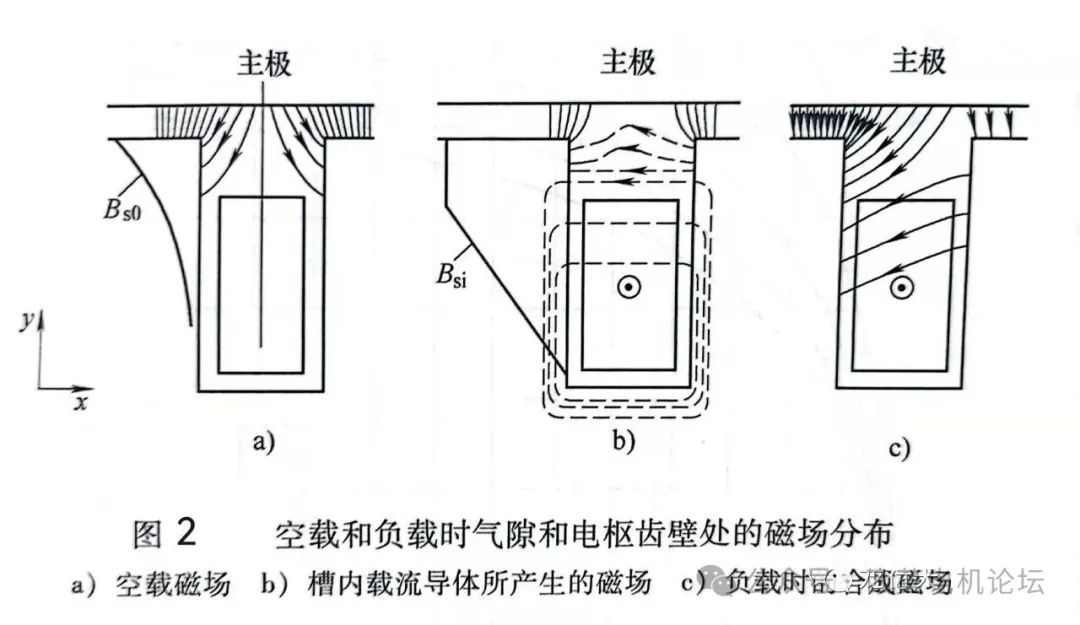
比較圖2a)和圖2c)可以看出：空載時電樞左、右齒壁上的磁場為對稱分布，作用在左、右齒壁上的法向(x方向)磁場力互相平衡，使切向合成磁場力和相應(yīng)的電磁轉(zhuǎn)矩為0。負(fù)載時，由于載流導(dǎo)體的作用，氣隙和槽內(nèi)的磁場發(fā)生畸變，左、右齒壁上的磁場分布不再對稱，左齒壁上的磁場加強、磁應(yīng)力加大，右齒壁上的磁場減弱、磁應(yīng)力減小，結(jié)果使齒上受到一個x方向（即切向）的磁場力和電磁轉(zhuǎn)矩。

設(shè)Bs0為空載時齒壁上的磁通密度，Bsi為槽內(nèi)載流導(dǎo)體單獨作用時，在左、右齒壁處所產(chǎn)生的磁通密度；則負(fù)載時左齒壁上的磁通密度Bs1＝Bs0＋Bsi，右齒壁上的磁通密度Bs2＝Bs0-Bsi，如圖2c)所示；于是由式(11)可知，作用于左、右齒壁上的合成磁應(yīng)力σ為：

σ≈(1/2μ0)(Bs12-Bs22)

=(1/2μ0)(Bs1+Bs2)(Bs1-Bs2)

=(1/2μ0)?2Bs0?2Bsi

=(2/μ0)Bs0?Bsi (17)

合成磁場力F則為

F=∫【0,h】σ?L dy=(2/μ0)L∫【0,h】Bs0Bsidy (18)

式中：h為槽高；L為鐵心有效長度。此力對齒壁而言是法向力，對電樞而言，則是產(chǎn)生電磁轉(zhuǎn)矩的切向力。

一般情況下，要用解析法來推導(dǎo)出Bs0和Bsi是極為困難的。但是，對于矩形開口槽、且槽形很深(認(rèn)為h→∞)，載流導(dǎo)體置于槽底的情況，可以用保角變換法來求出槽壁處的Bs0和Bsi，并由此算出作用在載流導(dǎo)體上的合成的磁場力F。對于這種特定情況，經(jīng)過一系列復(fù)雜的推導(dǎo)和計算(略)可得到如下結(jié)論：

①當(dāng)槽深h→∞時，作用在左、右齒壁上的合成磁場力大小，恰好等于電樞為光滑時作用在載流導(dǎo)體上的切向電磁力F0，F(xiàn)0＝BδIL，其中Bδ為光滑電樞時的空載氣隙磁密。

②從槽口到深度d處，齒壁上的合成磁場力Fd如圖3所示。

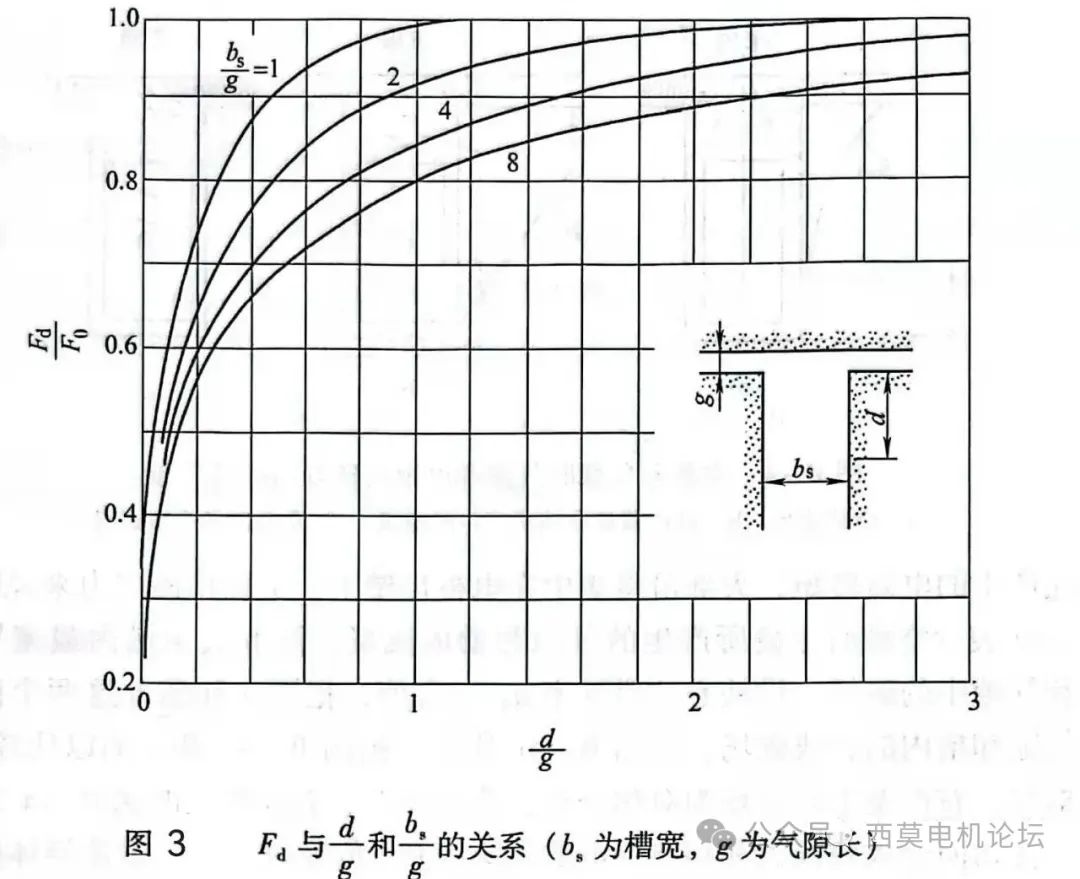
由圖可見，90％以上的磁場力將集中在離槽口2.5g深(g為氣隙長)的齒壁上。

③當(dāng)載流導(dǎo)體進(jìn)入槽內(nèi)時，由于齒的屏蔽作用，導(dǎo)體上所受到的切向電磁力將隨導(dǎo)體所處深度的增大而急驟下降。例如當(dāng)bs/g＝4、載流導(dǎo)體為線電流、進(jìn)入槽內(nèi)深度d＝2g時，作用在導(dǎo)體上的切向電磁力，將下降到置于光滑電樞表面時的10％左右。

用上述磁應(yīng)力法來計算磁場力，其優(yōu)點是既可算出實際磁場力的分布，又可算出總的電磁力和電磁轉(zhuǎn)矩；缺點是需要求出負(fù)載時整個電機(jī)內(nèi)的磁場分布，這用解析法是不可能做到的，只能通過數(shù)值計算的辦法才能做到。

必須強調(diào)一個重要結(jié)論：電樞開槽后，無論何種槽型，作用在電樞齒壁上的合成切向磁場力，與作用在槽內(nèi)載流導(dǎo)體上的切向電磁力兩者之和，恒等于載流導(dǎo)體置于光滑電樞表面時的切向電磁力“BIL”，這就意味著電樞開槽后，仍然可以用“BIL觀點”來計算切向電磁力！特別是如果僅需知道總的電磁轉(zhuǎn)矩，而無需得知電磁力和電磁轉(zhuǎn)矩的分布時，就可以作為載流導(dǎo)體置于光滑電樞表面的情況來處理，并用“BIL觀點”算出電磁力和總的電磁轉(zhuǎn)矩。但必須注意以下兩點：一是此時電樞表面必須是光滑的圓柱面，否則將導(dǎo)致錯誤的結(jié)果；二是這樣處理雖然總的切向電磁力和電磁轉(zhuǎn)矩結(jié)果是正確的，但是并未揭示問題的實質(zhì)和切向電磁力的分布情況，實際上電樞開槽后，產(chǎn)生電磁轉(zhuǎn)矩的切向力主要是作用在鐵心的齒上，而槽內(nèi)載流導(dǎo)體受到的切向力很小，通常可以忽略不計。

其實上述重要結(jié)論還可從另外一個角度，用“虛位移法”來理解和解釋：假設(shè)載流導(dǎo)體為“線電流”，即槽的面積遠(yuǎn)大于載流導(dǎo)體截面積，導(dǎo)體的粗細(xì)可以忽略，認(rèn)為載流導(dǎo)體是一根無限細(xì)的導(dǎo)線，當(dāng)把該載流導(dǎo)體放入很深的槽底時，則電機(jī)內(nèi)部的磁場分布(氣隙和槽內(nèi)的磁場分布)就與導(dǎo)體在槽底的切向位置無關(guān)，將載流導(dǎo)體在槽底切向移動位置時并不影響槽內(nèi)和氣隙磁場的分布，因而磁場的儲能不會因?qū)w在槽底作切向位移而變化，這就意味著磁場儲能對導(dǎo)體切向位移的偏導(dǎo)數(shù)為0，說明導(dǎo)體所受到的切向電磁力即為0。而鐵心若沿切向位移一個很小的角度時，磁場的儲能會變化很大，即磁場儲能對鐵心切向位移的偏導(dǎo)數(shù)很大，說明切向電磁力主要作用在鐵心上。當(dāng)然上述這種分析是建立在理想的假設(shè)條件下，如：“線電流”模型、槽子足夠窄而深、導(dǎo)體位于槽內(nèi)足夠深處等，如果考慮到實際電機(jī)中槽子深度有限、導(dǎo)體離槽口較近等因素，則槽內(nèi)載流導(dǎo)體也會受到一定的切向電磁力，特別是當(dāng)槽子寬而淺、導(dǎo)體離槽口很近時，導(dǎo)體受到的電磁力會有所增大(如圖3所示)，但與齒壁受到的切向力相比，導(dǎo)體受到的切向電磁力還是很小，可以忽略的。

總結(jié)一下：

①電樞表面光滑時，電樞受到的切向電磁力可以用“BIL觀點”來計算，切向電磁力的作用點是作用在載流導(dǎo)體上。因此在設(shè)計無槽電機(jī)時，要特別注意繞組與電樞鐵心之間的機(jī)械固定問題，必須要有足夠的附著力，以防線圈與鐵心之間扭脫打滑發(fā)生相對移位。

②電樞開槽后，線圈導(dǎo)體嵌放于槽內(nèi)，此時仍然可以用“BIL觀點”來計算總的切向電磁力的大小，但切向電磁力的作用點并不是作用在導(dǎo)體上，而是主要作用在鐵心的齒壁上，而槽內(nèi)載流導(dǎo)體上的切向電磁力可以忽略不計。因此，設(shè)計有槽電機(jī)時，應(yīng)該對齒根部位進(jìn)行必要的機(jī)械強度校核，以免齒根斷裂。





審核編輯：劉清