好多人都是因為這個地方放棄數學的對吧?
我覺得也不用說什么這個語言是怎么出來的,直接講我的理解。
“無限接近于X”這個表述方式無法被準確定義。你不能用一個未被定義的詞來作為定義本身的一部分。就好像我們寫程序一樣,一定要保證一開始運行的狀態你是可控的。
所以這個ε-δ的工作就是來精確的說明和一個數字無限貼貼的時候應該如何理性的定義。(把原來不確定的動態的靠近過程,轉換成了靜態的,確定的數)
其實本質是使用了差值,或是叫可以接受的誤差。
這里面說了數列和極限:

數列說的是下標,函數說的領域,因為我們研究的一點處的情況。
其實ε是"error"(誤差)、δ是"distance"(距離)的首字母。實際上,是柯西在他的著作中用ε來表示"error"的。
這個也挺抽象的

目前教科書上面的定義都是這個

wiki百科是這樣的,其實是一樣的
emmmm,原因是因為采用了‘任意-存在’這種邏輯結構,就讀不懂了。
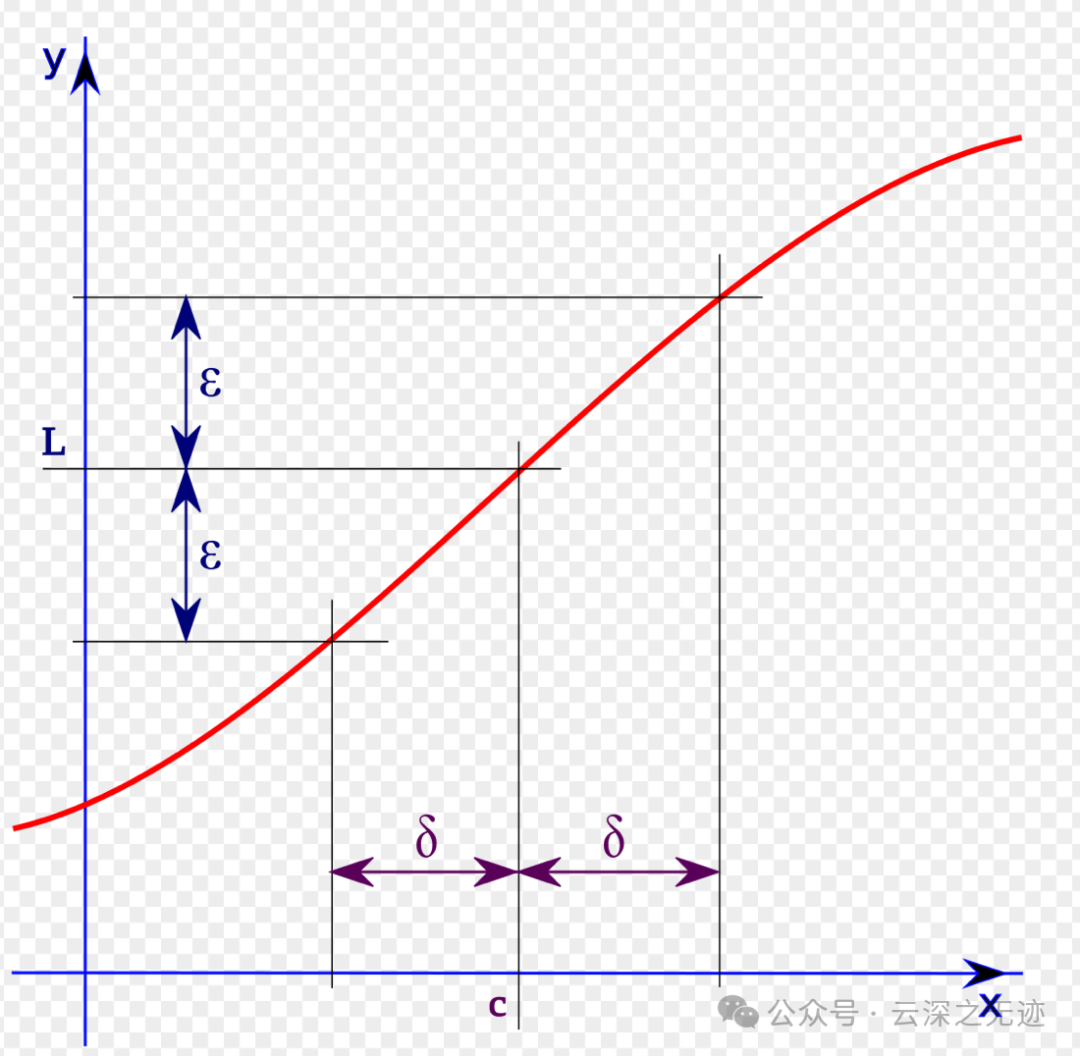
這個是上面的定義的可視化圖:只要無限靠近c,函數值就無限靠近L
繼續說,如何來表達函數值和極限值的趨近,也就是極限關系呢?就是它們的距離越來越小,距離的表示就是 |函數值-極限|,距離一定是正的,加絕對值,如果你說可以是負值,那我勸你還是不要GHS。
也就是說,小于世界上任何一個正數就好了,可能在你的認識里面這個數等于0就是最好的,不行啊,這樣一搞不就是是等式了。
那么我們這樣說,對任意一個ε(取很小的值),使得|函數值-極限| <ε就說明啦。以上是對函數值無限接近于極限值的描述。

接著就是來說明這個了,這個x為什么會被夾著。
極限是自變量趨于某個值的,這個趨近于的描述應該是一個過程,如何用數學來說明這個趨近的事實。兩個點不太行,只有連續才可以表示一個過程。在數學里面使用“區間”才可以表示連續的點。
先設x和a的初始距離為δ,在x靠近a或者是趨近的這個過程中,x和a之間的范圍始終在(0,δ)區間里面。
距離我上面說了,可以用差的絕對值來表示,也就是說自變量趨于某個值。
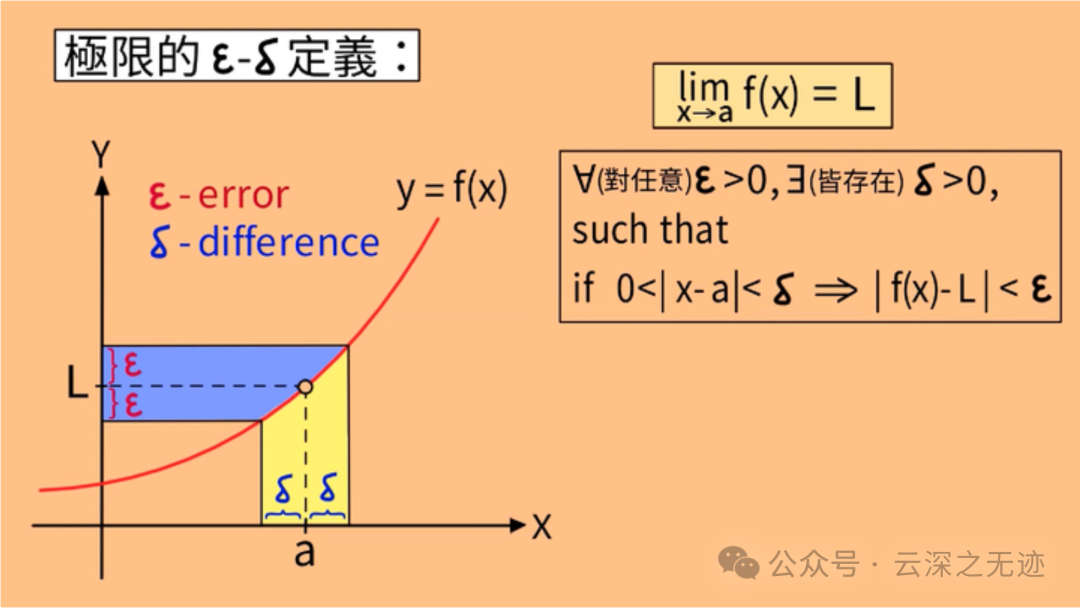
這個圖也挺形象
上面的這個不等式也可以說成是鄰域,也就是說鄰域知道了極限的作用范圍。
至于微積分基本上每個定義上,都會加個去心鄰域,現在明白了,其實就是為了防止鄰域中心沒有定義的情況,因為書上的定義定理啥的都得具有一般性,所以它就這樣,能夠代表所有不管在此點有沒有定義的函數,反正是極限,有沒有鄰域中心都一樣。
本來極限的定義就是無限趨向該點,這和在該點有沒有定義并沒有關系,所以我們只要保證除去該點以外的鄰域有定義即可。

這個解釋也很酷,說明了鄰域的作用其實是一個微小的觀察空間


這個也是一個有趣的例子
審核編輯:劉清
-
微積分
+關注
關注
1文章
26瀏覽量
8832
原文標題:極限語言ε-δ的理解
文章出處:【微信號:TT1827652464,微信公眾號:云深之無跡】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
關于NAND Flash調試的一點總結
一點接地,什么是一點接地,一點接地應注意的問題
路燈藍光危害你造嗎?專家建議“冷一點,暗一點”
一點理解之 CmBacktrace: ARM Cortex-M 系列 MCU 錯誤追蹤庫





 關于極限語言ε-δ的一點理解
關于極限語言ε-δ的一點理解












評論