在SSB單邊帶調制中,會用到RC-多相網絡,這個網絡非常有意思,在空間中是一個圓柱形,并不能用平面表示。這篇文章對RC-多相網絡原理進行了分析和理論推導。這里介紹給感興趣的同學。
本文分析了HA5WH相位移位網絡(phase shift network)。描述了具有循環對稱性的理想網絡,并提供了簡單的設計方程。通過考慮元件容差進行的計算表明,必須使用匹配良好的元件才能獲得高質量的結果。
目錄
1. 引言
單邊帶信號的產生或檢測的移相法需要在音頻頻率范圍內具有的相對相差的兩個信號。移相法一直不太受歡迎,特別是在相對便宜的濾波器出現之后。未來,數字信號處理技術大概率將執行必要的音頻相位移或直接生成射頻單邊帶信號。那么,為什么你還對音頻相移網絡感興趣呢?或許是因為它們較低的成本、易于構建,并且非常有趣。此外,筆者在這里描述的技術對于其他級聯網絡的有效分析也是非常有用的。
多年來,ARRL手冊[1]中包括了一個由HA5WH設計的音頻相移網絡電路。筆者還沒有找到這個網絡的原始參考文獻。手冊聲稱,該電路使用的公差元件,可以提供大約的邊帶抑制。這與通常的結果相悖,即你需要的元件來獲得約的抑制。在本文中,筆者將分析這類網絡并給出設計方程。不幸的是,這種分析表明,使用公差元件可能導致邊帶抑制不良。使用理想元件,網絡可以提供優異的性能,通過使用高公差元件或匹配良好的低公差元件,網絡仍然可以提供良好的性能。
在第2節中,筆者給出了邊帶抑制的一般公式,用相位和幅度誤差表示相位網絡中的邊帶抑制。在第3節中,筆者推導了一種有效的分析一般HA5WH型網絡的方法。第4節給出了對網絡理想實現的分析。第5節描述了用易于計算的橢圓函數對網絡進行優化,第6節給出了元件公差的影響。結果是一組簡單的設計方程,用于理想網絡,并估計了對元件公差的敏感性。附錄中列出了一組實現所述方法的Fortran程序。
2. 相位誤差對邊帶抑制的影響
移相法生成的單邊帶信號在數學上表示為,其中正負號分別表示上(下)邊帶,,是載波頻率。類似地,,是音頻調制頻率。余弦函數可以寫成
這是移相法的基本方程。右側的乘法是通過平衡調制器完成的,而且兩個音頻信號(以及兩個射頻信號)相位差必須為,且幅度相等。我們假設射頻信號恰好相位差為,且幅度相等。使用常規的復數表示法,其中表示一個音頻信號,表示另一個音頻信號,使用非理想的相移網絡的結果為
邊帶抑制(或增強)由下式給出:
注意,如果等于,即兩個信號的幅度相等,那么對于相位誤差,抑制(以分貝表示)簡單表示為:
3. 分析HA5WH網絡
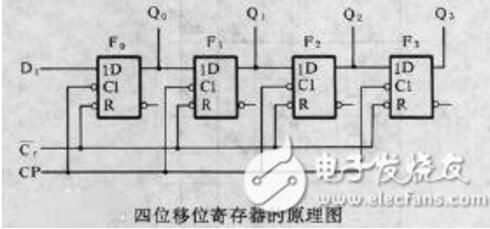
圖1給出了ARRL手冊中的HA5WH網絡的電路圖。有了這個電路,可以使用網孔或節點分析輕松地進行數值分析。這種暴力方法的缺點是它無法解釋網絡為何有效,或者網絡的變化如何影響其性能。因此,筆者將提出一種方法,這種方法在數值上更有效,而且通過使用理想網絡的對稱性,可以得出簡單的設計方程。
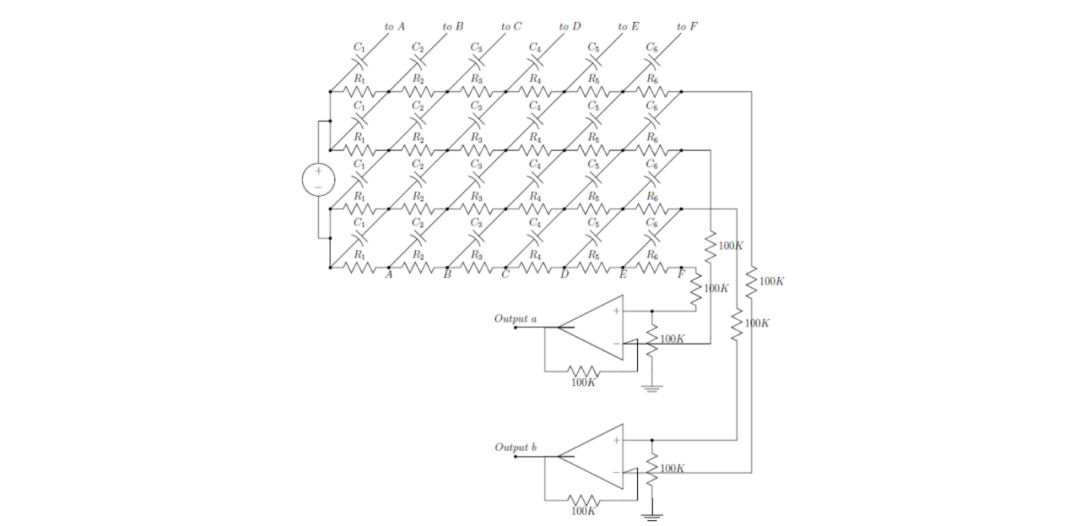
圖1:HA5WH寬帶相移網絡的示意圖。
顯然,該移相網絡由6個相似的部分組成,每個部分都有4個輸入連接和4個輸出連接。其中一部分如圖2所示。
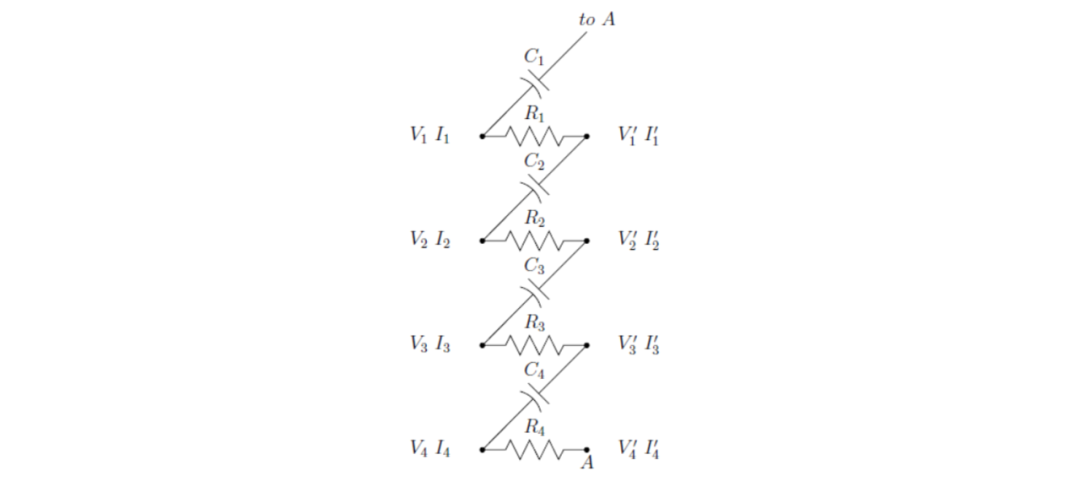
圖2:HA5WH網絡的一部分的示意圖。
將輸入電壓和電流標記為。相應的輸出電壓和電流標記為。對這個網絡直接進行節點分析,得到了由矩陣方程表示的8個線性方程:
其中是長度為4的向量,是4×4矩陣。式5緊湊地表示了網絡各節點處的電流守恒要求的8個方程。矩陣如下:
與使用矩陣級聯二端口網絡完全類似,為了級聯這些網絡部分,定義一個新的矩陣方程,解出矩陣得到,其中是矩陣的逆。
將網絡的每個部分的8x8矩陣標記為,將輸入與整個網絡輸出相關的矩陣是,由四個4x4矩陣組成,表示如下:其中是矩陣乘積。
手冊中的電路在4個輸出連接上4個負載電阻。將它們標記為,并定義一個的負載矩陣,
可以將輸出電壓和電流之間的關系寫為,
解出,然后進行反向代入,得到最終的網絡矩陣方程,它將4個輸出電壓與4個輸入電壓相關聯,
式中,式15中的1代表單位矩陣,
如果輸出電阻相對于其他電路阻抗來說很大,可以被視為零。在這種情況下,方程簡化為,
手冊中的網絡使與下式成正比,
在從電路數值計算得到和矩陣之后,輸出信號需要按以下方式組合,
邊帶抑制由式3給出。信號的相對幅度和相位也可以被計算出來。大多數相移網絡都是基于全通網絡的(all pass networks),因此所有信號的幅度都具有相同的衰減。但HA5WH網絡不是全通網絡。理想情況下,我們希望既有很好的邊帶抑制,又希望和在音頻電路的通帶范圍內保持恒定的幅度和相位。
如果被求逆的矩陣變為奇異矩陣,上述分析將在奇異點失效。例如,當在
在這些點附近,計算中的舍入誤差會很大。對于這里的分析,不是一個大問題。然而,在具有許多部分或接近奇異點的網絡上進行分析時,將需要采用的更多的數值計算技巧,或者使用標準公式,在該公式中一次性求解完整的網絡方程組。
4. 理想循環網絡的分析
如手冊所示,HA5WH網絡的設計在每個網絡的六個部分中都包括四個相同的電阻和四個相同的電容。這意味著該網絡在其端口順序的循環交換下是不變的。也就是說,如果我們通過將1變成2,2變成3,3變成4,4變成1來重新標記端口,我們將得到描述網絡的完全相同的方程。這種不變性通常使用群論的數學方法處理[2],這極大地簡化了對具有對稱性系統的研究。理想的HA5WH網絡具有所謂的循環4或對稱性。可以使用群論來分析網絡方程。對代表循環運算符的矩陣特征的分析表明,的4個不可約表示各出現一次。因此,它們對應于矩陣的4個特征向量,可以立即寫出這些向量。
然而,大多數無線電愛好者可能對群論不太熟悉,然而,可以在不使用群論的情況下輕松驗證這些結果。矩陣的右特征向量和特征值由以下方程確定,
即將特征向量與矩陣相乘后,得到的結果仍然是該特征向量,只是乘以了特征值。將矩陣乘以其中一個特征向量的效果就是將該特征向量乘以特征值。在我們的基礎上,循環特征向量是在元素之間具有恒定相位差的向量,且在最后一個元素與第一個元素之間的相位差也相同。這就有了以下關系,
通過直接的矩陣乘法,可以輕松驗證如果在網絡部分中所有的和值相同,這些向量就是所有矩陣的特征向量。這是循環4對稱性的直接結果。此外,由于矩陣是矩陣的乘積的組合,這些相同的向量也是矩陣的特征向量。由于可以表示為矩陣乘以的組合,如果我們將表示為四個特征向量的線性組合,將通過取相同的線性組合并將每個項乘以適當的特征值得到。網絡必須被設計為產生的相對相位差。
HA5WH網絡的輸入只包含上述的最后兩個特征向量,即
最后一行定義了相關的特征向量為和。此外,如果輸出阻抗相同并且運算放大器具有良好的共模抑制能力,輸出對于前兩個特征向量也不敏感。如果由于元件容差而破壞了循環對稱性,同時滿足這兩個條件將是有幫助的。
當輸入如式23所示時,輸出通常會是
而平衡調制器的兩個輸出將是
邊帶抑制(以分貝表示)使用式3為
因此,為了設計一個好的網絡,我們必須消除這最后的兩個特征向量中的一個。到目前為止的分析顯示了如何構建HA5WH網絡。特征向量在4個電壓上具有相等的幅度,并且在相鄰端口之間有和的相位差,最后一個相當于的相位差。我們希望選擇網絡驅動、連接和元件值,以選擇出兩個相位差的特征向量中的一個。另外,同樣的思想也可以用來設計一個相對相位差為的網絡,只需使用在群下不變的網絡,或者從群得到的相位差等。
選擇元件值的第一步是計算四個矩陣的特征值。通過直接相乘,得到
其中上標a或b表示特征值對應于特征向量或。
當輸入一個特征向量時,一個矩陣的作用是將式11中的矩陣替換為它們的特征值。經過一些代數運算,得到,
矩陣與成比例。如果我們向網絡部分提供和的線性組合,該部分相對于抑制的因子為
HA5WH網絡具有以下特性:在正頻率下,式30中的比值的幅度始終小于1,而在時恰好為零。第一個特性表明,額外的網絡部分只能改善輸出的相對相位差。第二個特性表示,我們可以通過選擇單個網絡部分的值來設置精確相位差的頻率。這兩個特性極大地簡化了網絡的設計和優化。
單一頻率下的邊帶抑制,對于一個包含個部分的網絡,其中第i個部分的值分別為和,可以表示為
選擇每個部分的值的簡單方法是使用計算機繪制上述結果,并調整和以達到所需的抑制效果。實際上,如果你試圖使用已經在你廢品箱中的一組零件進行設計,這是一個顯而易見的技術。然而,抑制效果的形式使得在下一節中看到的最佳值的選擇變得容易。
5. 優化邊帶抑制
的最佳值可以使用橢圓函數輕松計算。通常,我們希望最壞情況下的抑制效果盡可能高。這引導我們使用等紋波或切比雪夫逼近。相關數學方法的細節可以在Saraga的著作[3]中找到。對于上限頻率和下限頻率,個部分網絡的值為,
其中,表示第一類完整橢圓積分,是雅可比橢圓函數[4, 5]。
在表1中,給出了一些對業余愛好者來說可能感興趣的網絡的計算值,以及它們的理論邊帶抑制效果。這些理論結果當然是在假設元件完美的情況下得到的最佳情況。
順便提一下,注意到Saraga的泰勒逼近[3]是通過簡單地選擇所有的值相等,并且等于得到的。此外,如果在特定頻率(例如,如果您希望在單邊帶發射機中使用音頻音調產生頻率移鍵控)需要最大抑制效果,那么可以簡單地選擇適合這些頻率的值,然后優化其他網絡部分。
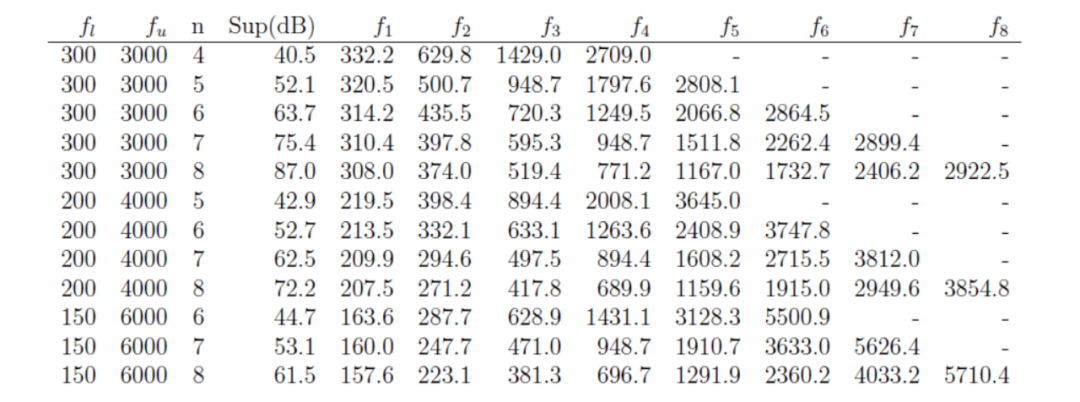
表1:一些理想的HA5WH類型相位網絡的最佳切比雪夫值。和分別為上限和下限頻率,是網絡的階數,,其中從1到,是精確相位差的頻率。相應的值為。Sup表示網絡范圍內最小的邊帶抑制效果,以分貝表示。
6. 振幅變化和元件容差的影響
到目前為止,只關注了兩個輸出之間的相對相位差。為了獲得高質量的音頻信號,網絡的輸出必須是平坦的。通常,這可以通過構建全通網絡來實現。由于HA5WH網絡不是全通形式,我們必須研究其頻率響應的衰減。在圖3、4和5中,分別繪制了為頻率范圍為到設計的最佳4、6和8部分濾波器的邊帶抑制效果,一個輸出信號的幅度和相位變化,這些濾波器使用相等阻值的電阻。網絡的各個部分按照值從大到小的順序排列,與原始的HA5WH設計一致。如圖所示,幅度變化小于,相位變化平滑,邊帶抑制效果符合預期的等紋波形式。
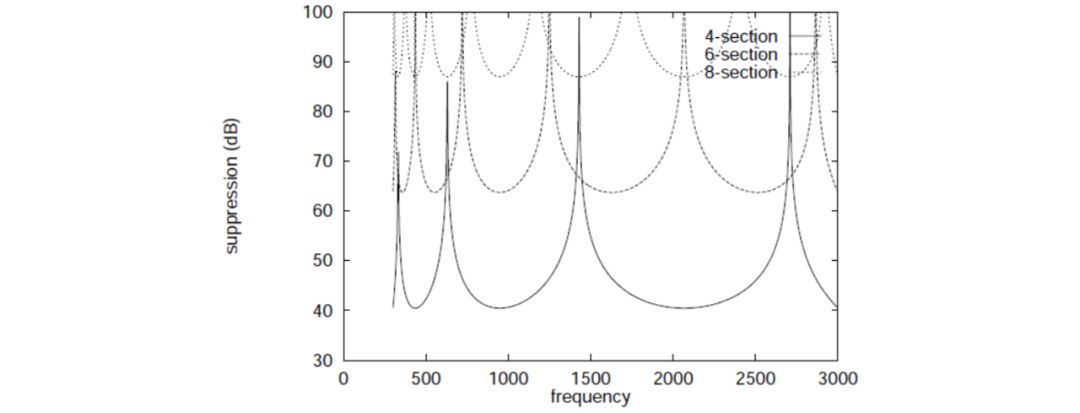
圖3:在頻率范圍為到時,4、6和8個最佳切比雪夫網絡的非期望與期望邊帶幅度的比率。
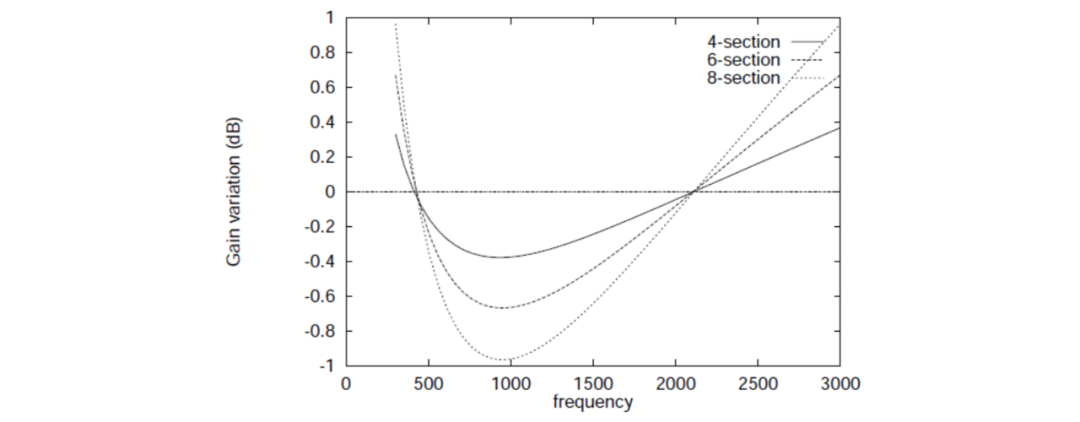
圖4:在頻率范圍為到時,4、6和8個最佳切比雪夫網絡的一個輸出信號的相對幅度。
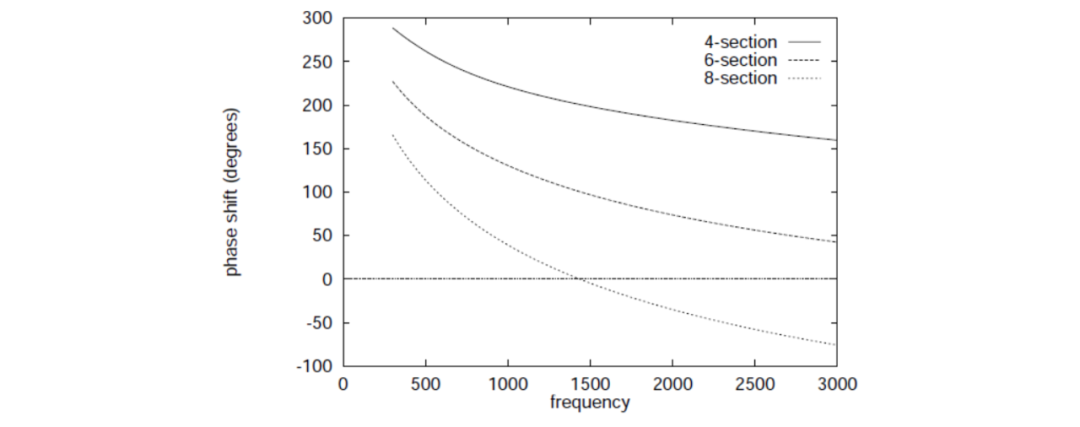
圖5:在頻率范圍為到時,4、6和8個最佳切比雪夫網絡的一個輸出信號的相位差。
該網絡在手冊中的主要優勢之一是聲稱可以使用低容差元件制造高性能網絡。從第5節的分析中,如果保持循環對稱性,網絡將在每個網絡部分對應的個選定頻率(即)處完美運行。由于一般來說元件的匹配比準確測量它們的值更容易,筆者研究了由于完全匹配但容差較低的元件引起的這些節點頻率變化的影響。由于電阻和電容都可能有變化,使用10%的元件可能會導致節點頻率的變化約20%,如果兩種元件的值都朝著同一個方向變化。最糟糕的情況是所有部分的頻率都比正常值高或低20%。這只是將網絡的中心頻率向上或向下移動20%。對于在到范圍內的最佳6部分濾波器而言,這將把邊帶抑制效果從超過降低到約。如果假設網絡節點頻率的變化為10%(即5%的元件),并且再次假定所有頻率變化的方向相同,抑制效果接近。這表明相對低容差但匹配良好的元件可以獲得出色的結果。當每個濾波器部分的元件是完全匹配的時,式31可以輕松用于預測由于元件容差導致的每個濾波器部分的值變化的影響。
當每個部分中使用不匹配的和值時,這當然是最具實際興趣的情況。在這種情況下,我們可以通過觀察當M矩陣不再是循環時,和之間的交叉項來了解最壞情況的可能性。典型的項給出了貢獻,如下所示:
或
其中,這里的下標表示網絡部分中的位置,如圖2所示。這表明,一個具有表示容差)的單個部分可以將總體抑制效果降低到大約。也就是說,如果網絡部分中的元件沒有匹配,那么的元件可能導致抑制效果降低到,的元件可能降低到。請注意,為了確保獲得60的相對抑制效果,需要使用短期和長期容差為的元件。作為對不匹配元件敏感性的具體例子,筆者計算了原始HA5WH 6部分濾波器的抑制效果,其中只有最后一節的電阻被改變了。和提高了,和降低了。對于理想元件,抑制效果大于。只改變最后一節的電阻將抑制效果降低到,與上面的簡單計算結果大致一致。利用這些結果嘗試構造近似最壞情況的情形,筆者嘗試以完全相同的方式改變每個部分中的所有電阻。此外,通過將和的值提高并將和的值降低來改變所有電容器的值。結果是進一步降低了不需要的邊帶抑制效果,降低到約。顯然,10%的元件和運氣不佳將產生不可接受的邊帶抑制效果。
7. 結論
HA5WH網絡利用循環對稱性提供了簡單的設計方程,并且在理想元件下具有出色的邊帶抑制效果。如果保持循環對稱性,網絡對于元件公差不太敏感。這意味著每個網絡部分的元件應該被精心匹配。通過使用不匹配的元件打破循環對稱性可以嚴重影響網絡的性能。
8. 勘誤和附錄
在發表本研究報告后,筆者受到了Gingell(KN4BS)的聯系,他告訴筆者說他是這個電路的發明者,也是類似電路中稱為“A Symmetrical Polyphase Network”的其他電路的發明者。他對筆者在這里提到的大多數結果都有所了解,除了Saraga的方法應用于形成Chebychev網絡的部分可能例外。然而,他告訴筆者,Saraga是他的博士答辯委員之一,所以筆者認為Saraga的方法對他并不完全陌生。
以下是他發送給筆者的一些參考文獻,其中包含了更多的歷史背景。
1. M.J.Gingell: “A Symmetrical Polyphase Network” British Patents 1,174,709 and 1,174,710 filed 7th June 1968, published 17 Dec 1969, US Patents 3,559,042 and 3,618,133 published Jan 261971 2. M.J.Gingell: “Single Sideband Modulation using Sequence Asymmetric Polyphase Networks” Electrical Communication Magazine, Vol 48 No 1 and 2 combined 1973, p 21-25
2. Pat Hawker, G3VA: “Polyphase System for SSB Generation” in “Technical Topics” Radio Communication Oct 73, p698-9
3. Pat Hawker, G3VA: “More on Polyphase SSB” in “Technical Topics” Radio Communication Dec 73, p852-853
4. M.J.Gingell: “The Synthesis and Application of Polyphase Networks with Sequence Asymmetric Properties” PhD Thesis University of London, 1975
5. M.J.Gingell: “Sequence Asymetric Polyphase Networks: Application to F D M” IEE Colloquium on Applications of Active, Digital and Passive Filters, London, January 141975.
6. Pat Hawker, G3VA: “G3PLX polyphase SSB generator” in “Technical Topics” Radio Communication May 1975, p379-381
7. A. Gschwindt, HA5WH: “Some Reflections on the four-way phasing method” Radio Communication Jan 76, p28-33
8. J.R.Hey: “Practical Polyphase SSB for shallow pockets” Radio Communication Sept 76, p656-660, 663
9. J Heyne: “New Active Quadrature Phase Shift Network” IEE Electronics Letters, 31 March 1977, p216-218
10. A G Constantinide: “Digital Phase Splitting Network Design for digital F.D.M. applications” PROC IEE, Vol 23 No 12 Dec 1976, p 1313-1315
審核編輯:黃飛
-
射頻
+關注
關注
104文章
5586瀏覽量
167769 -
濾波器
+關注
關注
161文章
7822瀏覽量
178162 -
數字信號處理
+關注
關注
15文章
560瀏覽量
45864
原文標題:相移網絡分析與優化
文章出處:【微信號:電路設計小工具,微信公眾號:電路設計小工具】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
一文解析Matlab如何實現移位寄存器
FPGA中UART控制器的移位寄存器模塊的實現方式
PNA-X相位參考校準關于LO而不是RF的變化
相位噪聲問題
偏離線性相位程序錯誤地表征了DUT
一文解析什么是無線傳感器網絡
74HC595 8位移位寄存器的相關資料分享
74HC165中文資料 (8位移位寄存器)
HA-2544 pdf datasheet (50MHz,
史上最全-5G可使用的波形有哪些?
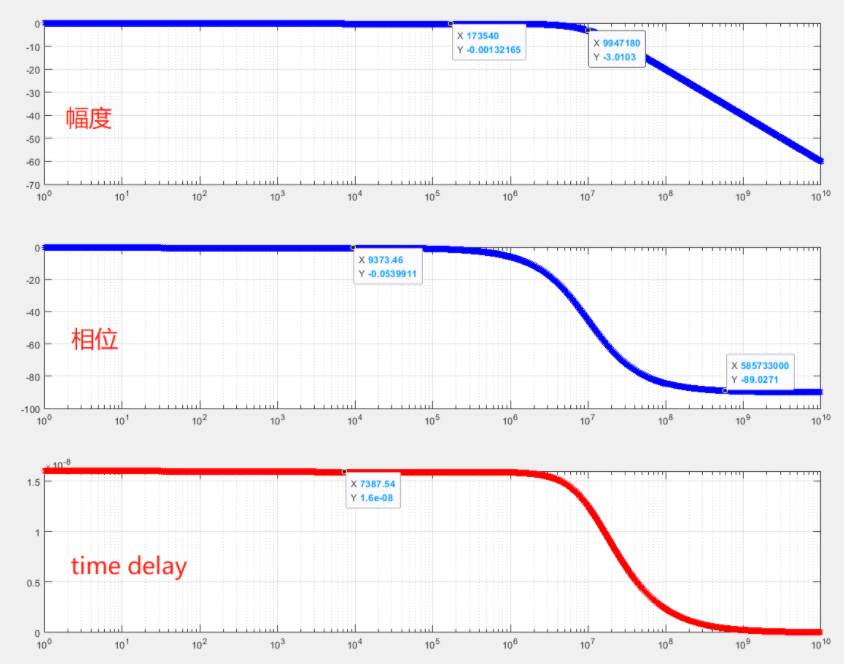
淺談信號delay time和phase shift




 一文解析HA5WH相位移位網絡(phase shift network)
一文解析HA5WH相位移位網絡(phase shift network)










評論