信號處理(Signal Processing)是對各種類型的電信號按各種預期的目的及要求進行加工過程的統稱。它涵蓋了模擬信號處理和數字信號處理兩大領域。模擬信號處理主要關注對連續變化的模擬信號的處理,而數字信號處理則是對離散的數字信號進行處理。
信號處理的主要目的是提取信號中的有用信息。在這個過程中,信號可能會經歷放大、濾波、去抖動、采樣和重建等多種處理方法。例如,濾波可以通過特定的濾波器去除信號中的噪聲或干擾,使原始信號更加清晰和準確。放大則通過放大電路增加信號的幅度,以提高信號的分辨率和檢測靈敏度。去抖動方法如時鐘同步、滑動平均和滯后濾波等,用于恢復信號的穩定性和準確性。采樣和重建是數字信號處理中的關鍵步驟,用于將連續信號離散化為離散信號,同時保持信號的完整性和準確性。
信號處理常用算法簡介
(1)變分模態分解(Variational Mode Decomposition,縮寫VMD):模態分解認為信號是由不同“模態”的子信號疊加而成的,而變分模態分解則認為信號是由不同頻率占優的子信號疊加而成的,其目的是要把信號分解成不同頻率的子信號。
該算法,是目前超好用、普遍常用的算法。
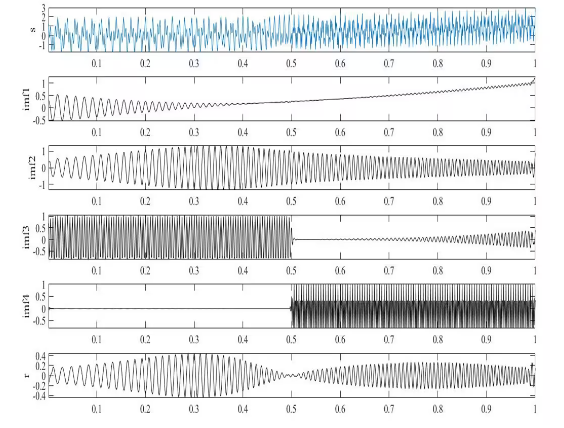
變頻變幅信號作變分模態分解,得到4個固有模態函數imf1~4及余項r
(2)經驗模態分解(Empirical Mode Decomposition,縮寫EMD):是由黃鍔(N. E. Huang)與其他人于1998年創造性地建立的一種自適應信號時頻處理方法,特別適用于非線性非平穩信號的分析處理。
該算法,是目前好用、常用的算法,僅次于變分模態分解算法。

有周期成分和間歇成分的分段信號作經驗模態分解,得到4個固有模態函數imf1~4及余項r
(3)小波分析(Wavelet):也叫“小波變換”,它通過伸縮和平移兩種處理對信號(函數)逐步進行多尺度細化,最終達到在信號高頻處實現按時間細分,在信號低頻處實現按頻率細分,能自動適應時頻信號分析的要求,從而可聚焦到信號的任意細節,解決了Fourier變換的困難問題,成為繼Fourier變換以來在科學方法上的重大突破。有人把小波變換稱為“數學顯微鏡”。
該算法,比較陳舊,被前人用得較多。但仍然是目前好用、常用的算法,僅次于變分模態分解算法、經驗模態分解算法。
(4)傅里葉變換(Fourier transform,縮寫FT):有多個中文譯名,常見的有“傅里葉變換”、“付立葉變換”、“傅立葉轉換”、“傅氏轉換”、“傅氏變換”、等等。
傅立葉變換是一種分析信號的方法,它可以分析信號的成分,也可用這些成分合成信號。許多波形可作為信號的成分,比如正弦波、方波、鋸齒波等,傅立葉變換用正弦波作為信號的成分。
該算法,不陳舊、特經典,被前人和現人用得最多。仍然是目前超好用、普遍常用、必不可少的算法。
信號處理在多個領域都有廣泛的應用。在移動通信中,數字信號處理技術能夠實現信號的調制、解調和濾波,確保信號的穩定傳輸。在圖像處理領域,數字信號處理技術可以用于圖像增強、壓縮和識別等。在聲音處理領域,數字信號處理技術可以實現對音頻信號的壓縮編碼,提高音頻的傳輸效率和存儲空間。此外,在雷達和聲吶、醫學成像等領域,數字信號處理技術也發揮著重要作用。
隨著科技的進步,一些新的技術和產品也開始應用于信號處理領域。例如,RD芯片作為一款可重構的數字信號處理器,能夠根據不同需求進行自我調整,實現處理效率和質量的雙重提升。它在5G技術、圖像處理、音頻處理等領域展現出強大的實力,為用戶帶來更加細膩、清晰的視聽體驗。
審核編輯:黃飛
-
算法
+關注
關注
23文章
4625瀏覽量
93141 -
數字信號處理
+關注
關注
15文章
562瀏覽量
45934 -
信號處理
+關注
關注
48文章
1037瀏覽量
103347 -
函數
+關注
關注
3文章
4344瀏覽量
62835 -
傅立葉變換
+關注
關注
3文章
105瀏覽量
32437
發布評論請先 登錄
相關推薦




 信號處理常用算法簡介
信號處理常用算法簡介











評論