媽耶,兜兜轉轉我都敢學信號與系統了。
第一節先要說明白能量的定義,里面信號幅值的平方有一種大家都知道怎么來的,就我不知道的感覺。
看了資料是這樣:
將信號f(t)施加在1歐姆電阻上,他所消耗的瞬時功率為|f(t)|的平方,這里的R就是1了,所以就是平方的形式:

首次登場,歸一化就是把分母設置為1,這也太騷了
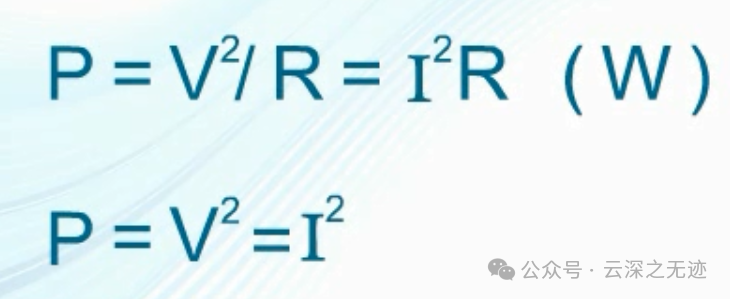
這個是我們電學里面的定義

把每一刻的功率都加起來就是能量:功率可以看作是單位時間內的能量
能量就是信號的平方在區間(-∞,+∞)上的積分。 功率就是能量與“無窮長的時間”的比值。
功率和能量,它們之間的關系反映了信號在時間或時間序列上的能量分布和傳輸效率。是不是這樣說話很裝逼的感覺?

這個不知道有沒有講明白
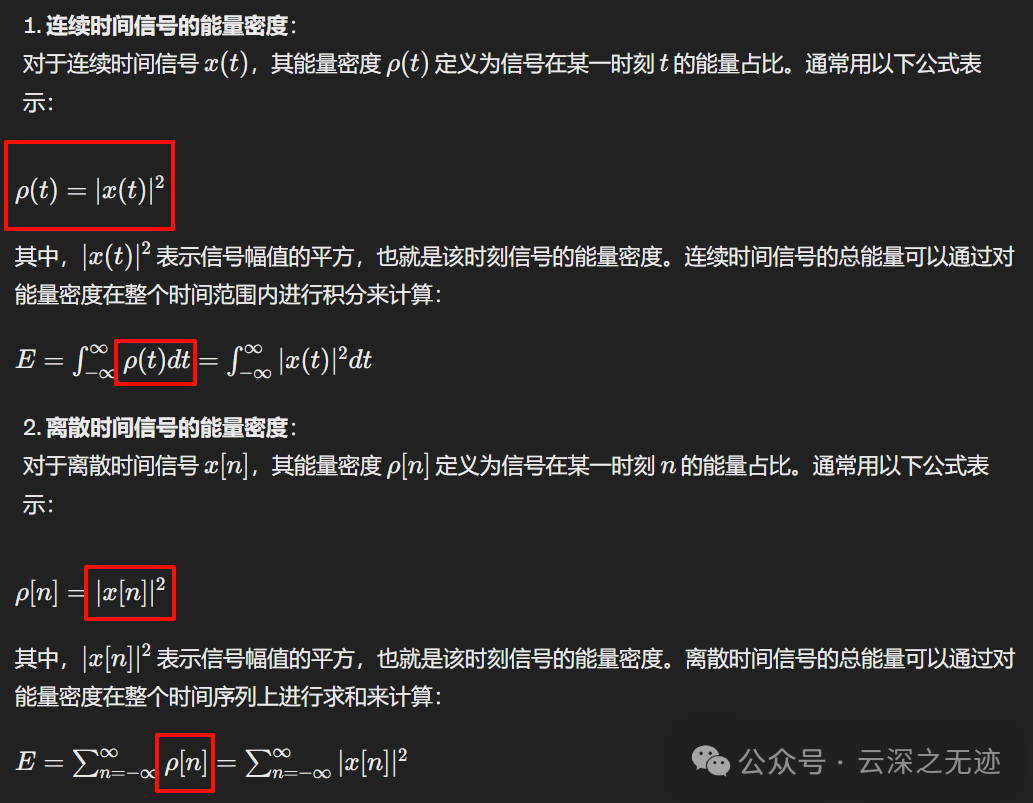
定積分-黎曼和的極限,反正就是把這些能量都收集起來的意思
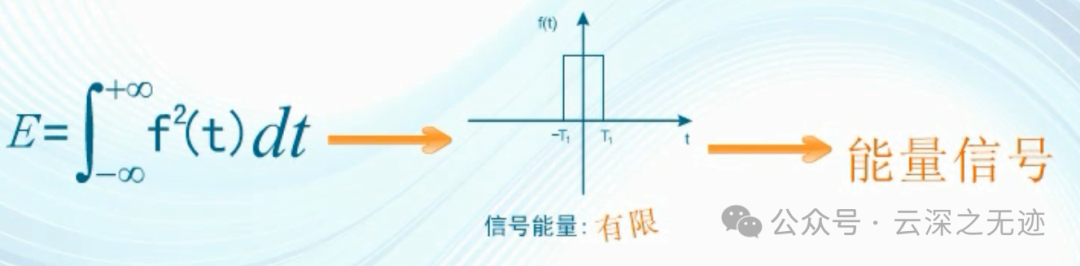
能量信號是指其能量有限且非零的信號
為什么要這樣表示?
物理意義:信號的能量與其幅值相關,而信號的幅值的平方與能量更直接相關。信號的幅值的平方代表了信號在某一時刻或時間段內的功率,而能量則是功率在整個時間范圍內的累積。
非負性:信號幅值的平方始終為非負值,這樣可以確保能量和能量密度始終是正數或零。這樣的定義更符合物理意義,因為能量本身不可能是負數。
計算便捷:信號的幅值的平方在數學上更容易處理。對于連續時間信號,計算平方后可以直接進行積分;對于離散時間信號,計算平方后可以直接進行求和。這樣可以簡化能量和能量密度的計算過程。
功率計算:在很多情況下,我們對信號的功率更感興趣。信號的功率是指信號在單位時間或單位頻率內的能量,而信號的幅值的平方恰好表示了單位時間或單位頻率內的功率。

這種能量無限,但平均功率有限的信號稱為功率信號,通常,周期信號都是功率信號。
能量:能量表示信號在整個時間或時間序列上的總累積能量,它是存在的,并且不受時間的影響。即使信號的能量消失,其能量仍然存在,因為能量是對信號波動幅值的平方進行積分或求和得到的。因此,無論信號的波動如何變化,能量都是一個固定的值,代表了信號的總體能量狀態。
功率:功率表示信號在單位時間或單位頻率內的能量傳輸或消耗速率,它的計算涉及到時間因素。 功率可以分為短時功率和長時功率兩種情況:
短時功率:對于某個時間段內的信號,可以計算其短時功率,即單位時間內的能量。
長時功率:對于無限長時間的信號,其長時功率可以近似看作是零,因為長時間內的能量傳輸或消耗速率會將總能量分配得非常稀疏,趨近于零。
能量有限、功率為零的信號為能量信號。
能量無限、功率有限的信號為功率信號。
代表波形一:一個無限延伸的正弦波
代表波形二:無限長的白噪聲
所有周期信號都是功率信號;所有有限數量的脈沖信號都是能量信號。
還有一說是:所有有界的周期信號都是功率信號。
審核編輯:劉清
-
正弦波
+關注
關注
11文章
645瀏覽量
55427 -
脈沖信號
+關注
關注
6文章
399瀏覽量
36994 -
離散時間信號
+關注
關注
0文章
5瀏覽量
2874
原文標題:信號與系統-能量定義
文章出處:【微信號:TT1827652464,微信公眾號:云深之無跡】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
能量采集系統超低功率的設計挑戰
淺析嵌入式系統的定義及其應用
淺析微電網能量管理系統的應用





 信號與系統-能量定義淺析
信號與系統-能量定義淺析











評論