BP神經網絡算法,即反向傳播(Backpropagation)神經網絡算法,是一種多層前饋神經網絡,通過反向傳播誤差來訓練網絡權重。BP神經網絡算法在許多領域都有廣泛的應用,如圖像識別、語音識別、自然語言處理等。本文將詳細介紹BP神經網絡算法的基本流程,包括網絡結構、激活函數、前向傳播、反向傳播、權重更新和訓練過程等。
- 網絡結構
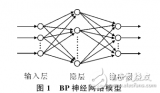
BP神經網絡由輸入層、隱藏層和輸出層組成。輸入層接收外部輸入信號,隱藏層對輸入信號進行非線性變換,輸出層產生最終的輸出結果。每個層由多個神經元組成,神經元之間的連接權重需要通過訓練學習得到。
1.1 輸入層
輸入層的神經元數量與問題的特征維度相同。輸入層的主要作用是將原始數據傳遞給隱藏層。
1.2 隱藏層
隱藏層是BP神經網絡的核心部分,可以有多個。隱藏層的神經元數量可以根據問題的復雜性進行調整。隱藏層的主要作用是對輸入信號進行非線性變換,提取特征信息。
1.3 輸出層
輸出層的神經元數量與問題的輸出維度相同。輸出層的主要作用是將隱藏層的輸出結果轉換為最終的輸出結果。
- 激活函數
激活函數是BP神經網絡中的關鍵組成部分,用于引入非線性特性,使網絡能夠學習復雜的函數映射。常見的激活函數有Sigmoid函數、Tanh函數和ReLU函數等。
2.1 Sigmoid函數
Sigmoid函數的數學表達式為:f(x) = 1 / (1 + e^(-x))。Sigmoid函數的輸出范圍在(0, 1)之間,具有平滑的曲線和連續的導數。
2.2 Tanh函數
Tanh函數的數學表達式為:f(x) = (e^x - e^(-x)) / (e^x + e^(-x))。Tanh函數的輸出范圍在(-1, 1)之間,具有零中心的特性。
2.3 ReLU函數
ReLU函數的數學表達式為:f(x) = max(0, x)。ReLU函數在x大于0時輸出x,小于0時輸出0。ReLU函數具有計算簡單、訓練速度快的優點。
- 前向傳播
前向傳播是BP神經網絡算法的核心過程,包括輸入信號的傳遞、激活函數的計算和輸出結果的生成。
3.1 輸入信號傳遞
輸入信號首先傳遞到輸入層,然后通過權重矩陣與輸入層神經元的連接傳遞到隱藏層。
3.2 激活函數計算
隱藏層和輸出層的神經元接收到輸入信號后,通過激活函數進行非線性變換。激活函數的選擇取決于問題的特點和網絡結構。
3.3 輸出結果生成
輸出層的神經元接收到隱藏層的輸出信號后,生成最終的輸出結果。輸出結果可以是分類標簽、回歸值或其他形式。
- 反向傳播
反向傳播是BP神經網絡算法的關鍵步驟,用于計算網絡誤差并更新權重。
4.1 誤差計算
首先,需要計算網絡輸出與真實值之間的誤差。誤差的計算方法取決于問題類型,如均方誤差、交叉熵誤差等。
4.2 誤差反向傳播
將誤差從輸出層反向傳播到隱藏層,計算每個神經元的誤差梯度。誤差梯度的計算依賴于激活函數的導數。
4.3 權重更新
根據誤差梯度和學習率,更新網絡中所有連接的權重。權重更新的目的是最小化網絡誤差,提高預測精度。
- 權重更新方法
權重更新是BP神經網絡算法的核心,常用的權重更新方法有梯度下降法、動量法和自適應學習率法等。
5.1 梯度下降法
梯度下降法是最基本的權重更新方法,通過計算誤差梯度并乘以學習率來更新權重。梯度下降法簡單易實現,但容易陷入局部最優解。
5.2 動量法
動量法在梯度下降法的基礎上引入了動量項,可以加速權重的更新速度并減少震蕩。動量法在訓練過程中具有更好的收斂性能。
5.3 自適應學習率法
自適應學習率法根據網絡的訓練情況動態調整學習率,如AdaGrad、RMSProp和Adam等。自適應學習率法可以提高訓練效率并避免陷入局部最優解。
-
圖像識別
+關注
關注
9文章
521瀏覽量
38314 -
BP神經網絡
+關注
關注
2文章
115瀏覽量
30580 -
語音識別
+關注
關注
38文章
1742瀏覽量
112767 -
輸入信號
+關注
關注
0文章
461瀏覽量
12587
發布評論請先 登錄
相關推薦




 BP神經網絡算法的基本流程包括
BP神經網絡算法的基本流程包括











評論