一、
什么是OCT?
光學相干斷層掃描(OCT)是一種三維成像技術,可以在散射介質中進行高分辨率成像,無需接觸樣品或使用任何耦合介質。OCT的橫向成像分辨率可達到幾微米,成像深度可達幾毫米。OCT能夠提供樣品表面輪廓和次表面結構(即表面以下的結構)及樣品均勻性的信息,從而實時提供準確的信息用于診斷、監測和現場過程反饋。因此,OCT已經在眼科、皮膚科、血管造影等生物成像領域得到了應用,并且在材料檢測和無損檢測中作為超聲波的強大替代技術。
二、
OCT的工作原理
OCT依賴于樣品不同區域的背向散射光來生成3D圖像。它使用不同的定位技術來獲取軸向(沿光束方向或進入樣品的z軸)和橫向(垂直于光束的平面或樣品的x-y軸)信息。軸向信息是通過估計從樣品中的結構或層反射的光的時間延遲來獲得的。這種技術類似于生成超聲波圖像的技術,但使用的是光而不是聲音。由于光速極快,直接測量反向散射光的時間延遲并不容易。因此,OCT系統使用低相干干涉技術間接測量時間延遲。
01
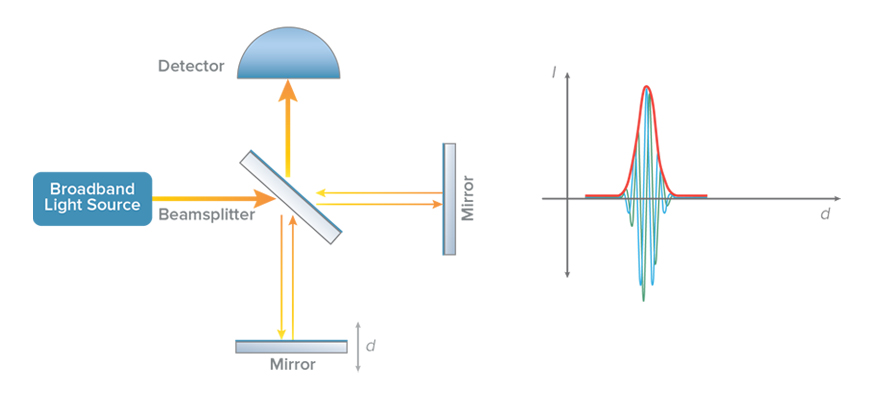
移動參考臂實現OCT測量
在低相干干涉儀中,使用具有寬光譜帶寬的光源進行照明。光源發出的光被分束器分成兩條路徑,稱為參考臂和樣品臂。來自每條臂的光被反射并在檢測器處結合。只有當參考臂和樣品臂的光程幾乎相等時,檢測器上才會出現干涉效應。因此,干涉現象的出現可以被用來進行光程的相對測量。
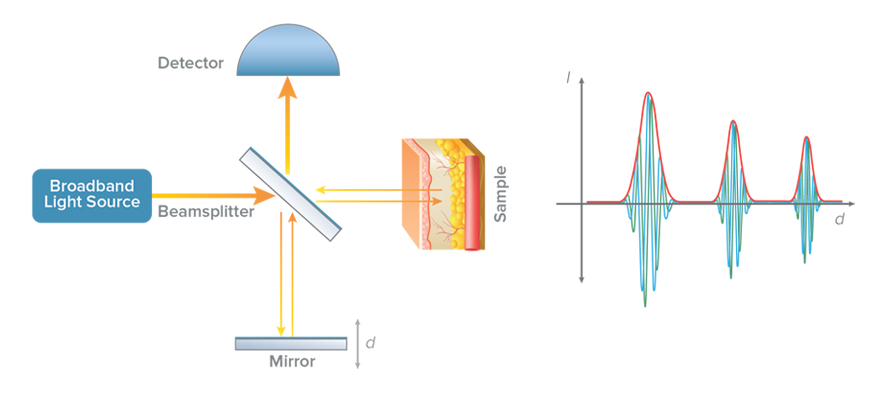
光學相干斷層掃描就是將樣品臂中的鏡子替換為待成像的樣品。然后對參考臂進行掃描,并在檢測器上記錄得到的光強度。當鏡子幾乎與樣品中的某個反射結構等距時,會出現一定的干涉圖案,從而獲得樣品對應位置的結構信息。顯然在參考鏡移動的過程中,兩次干涉發生對應的參考鏡位置之間的距離對應于測量光路中樣品兩個反射結構之間的光學距離。當光束穿過樣品時,不同的位置的獨特結構會通過上述低相干干涉記錄的反射量被記錄下來,從而得到測量樣品的散射信號和深度之間的函數關系。
把 OCT 中使用的寬帶光源光束聚焦到一個小點(約幾微米),并在樣品上進行x-y掃描,同時使用干涉測量收集深度信息,這樣可以構建樣品的完整 3D 圖像。
02
傅里葉域OCT
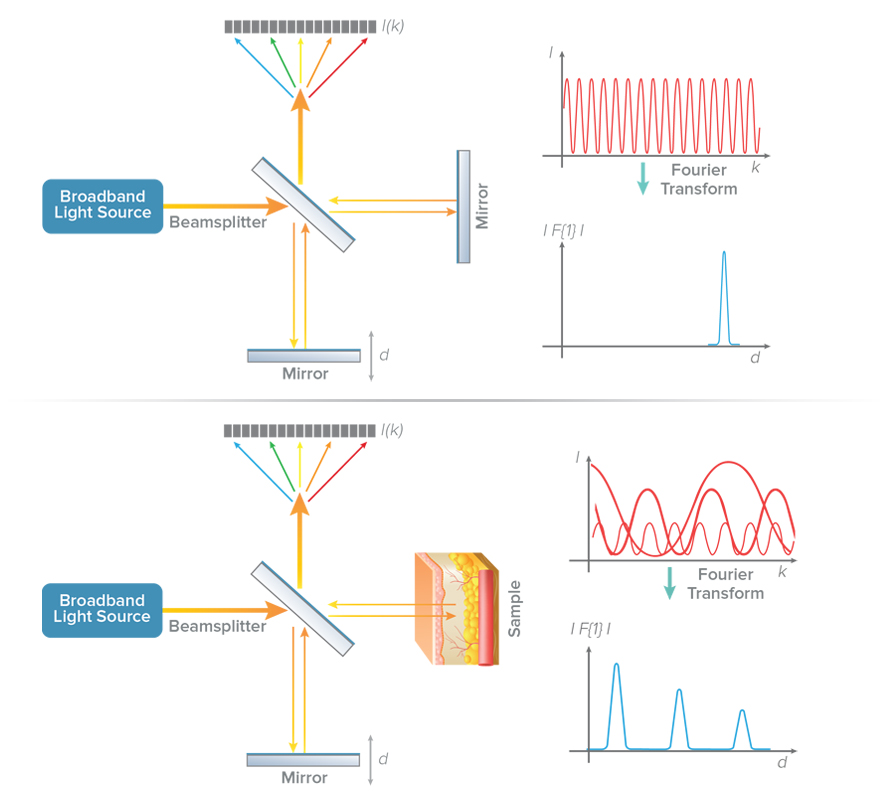
傅里葉域OCT(FD-OCT)提供了一種更高效的方法來實現上述低相干干涉。傅里葉域OCT(FD-OCT)并不是像上邊提到方法那樣在參考鏡的不同位置記錄強度,而是將強度記錄為光的波長(或頻率=光速/波長)的函數。不同頻率的光強度變化率反映樣品中不同反射層的位置信息。可以證明,光譜干涉數據的傅里葉變換提供的信息相當于移動參考鏡所獲得的信息。
03
傅里葉域OCT測量光譜干涉的兩種常用方法
光譜域光學相干斷層掃描(SD-OCT:Spectral Domain Optical Coherence Tomography):寬帶光源向樣品發出包含很多多波長成分的光譜管,并使用光譜儀同時測量所有波長。
·掃頻源光學相干斷層掃描(SS-OCT:Swept Source Optical Coherence Tomography):光源在一系列波長范圍內進行掃頻,檢測器的時間輸出被轉換為光譜干涉。
傅里葉域OCT相對于干涉儀中樣品臂鏡的移動擁有更快的成像速度,因為樣品的所有反射都被即時的同時測量出來的。傅里葉域OCT引入的速度提升為該技術開辟了全新的應用領域。通過商業化的設計,傅里葉域OCT可以輕松獲得實時視頻、面下OCT成像,使其廣泛用于用于諸如過程監控和手術引導等對實時性要求比較高的領域之中。
三、
OCT系統的關鍵參數
01
分辨率
OCT系統的軸向和橫向分辨率是獨立的。
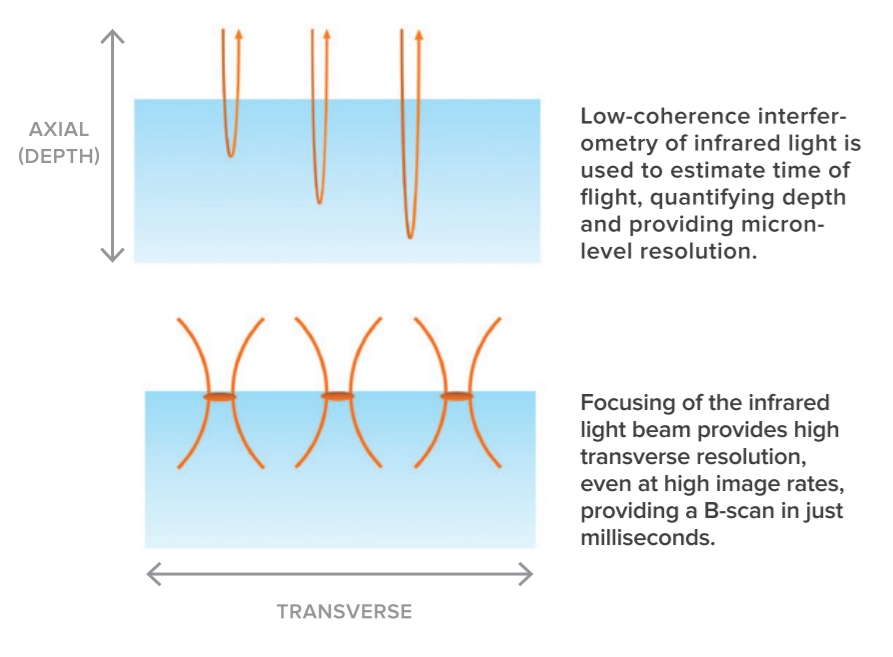
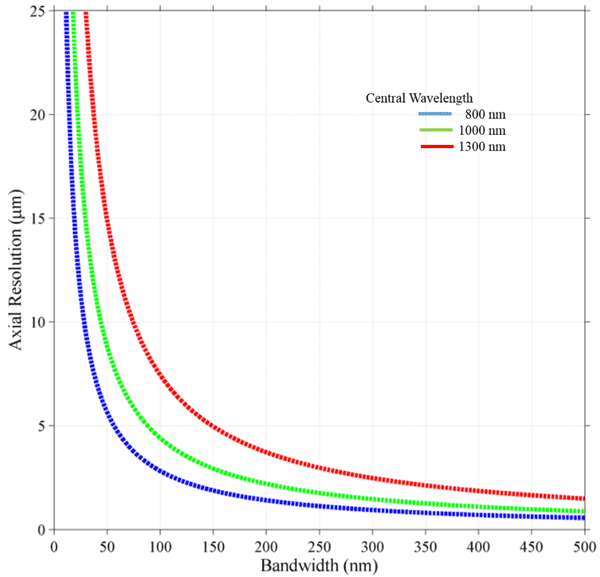
軸向(深度)分辨率與光源的帶寬(相干長度)有關。對于高斯形光譜,軸向分辨率 (λc) 由以下公式給出:

其中:λ是中心波長,Δλ 是光源的帶寬。
需要注意的是,這個光譜是指在探測器上測量到的光譜,可能與光源的發射光譜不同,這是由光學元件和探測器本身的響應造成的影響所致。需要注意的是,嚴格來講上述公式僅適用于高斯形光譜,對于其他光譜形狀僅可作為一個分辨率估算參考。對于任意已知形狀的光譜,應估算軸向擴展函數以了解可實現的分辨率和可能的邊帶。下圖中的軸向分辨率方程的圖顯示了三個不同中心波長的情況,展示了光源帶寬對近紅外常用工作帶中的軸向分辨率的影響。
02
成像深度
OCT(光學相干斷層成像)的成像深度主要受光源在樣品中的穿透深度限制。此外,在傅里葉域OCT中,深度還受到光譜儀有限像素數和光學分辨率的限制。如前所述,傅里葉域OCT中的圖像是在傅里葉變換光譜干涉數據后獲得的。傅里葉變換后的總長度或深度受光譜數據采樣率的限制,并遵循奈奎斯特定理。
具體來說,光譜數據采樣率(或采樣密度)指的是在給定的波長范圍內,光譜儀所能分辨和記錄的波長點的數量。更高的采樣密度意味著在相同的波長范圍內有更多的采樣點,從而可以獲得更高的分辨率和更大的成像深度。
由N個像素采樣的總帶寬(Δλ)給出了波長采樣率δλ = Δλ/N。由于傅里葉變換將頻率與時間關聯起來,我們可以將波長轉換為頻率,δν = cΔλ /λ2。奈奎斯特定理表明,傅里葉變換數據中的最大時間延遲將是tmax = 1/2 δν,而數據中的最大深度將是zmax = c* tmax。通過結合這些,傅里葉域OCT中可實現的最大成像深度為:
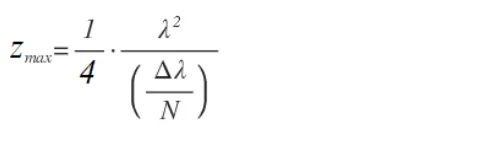
03
靈敏度隨深度的變化關系
在傅里葉域OCT中,理論上靈敏度取決于反射目標的位置。最大靈敏度出現在樣品光和參考光之間光程正好相等的點,即零延遲差點附近,并且隨著我們遠離零延遲點而減小。這種損失是由光譜儀的有限像素大小和有限光學分辨率導致的。可以證明,靈敏度與深度的關系如下:
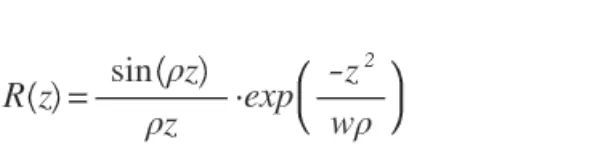
其中
R(Z):隨深度變化的靈敏度。
z: 深度,通常指光在樣品中傳播的距離。
ρ: 一個與光譜儀分辨率和光源帶寬相關的常數,具體定義依賴于系統的設計。
W=δλ/Δλ: 其中δλ是波長采樣率(光譜儀的分辨率),Δλ是總帶寬
sin(ρz): 表示由于光譜儀有限像素引起的調制效應。
sin(ρz)/(ρz):表示由于有限像素引起的調制效應的歸一化形
exp[-z^2/(wρ)]: 指數衰減項,表示由于光譜儀有限光學分辨率引起的衰減效應。
通過這個公式可以看出,OCT的靈敏度隨著分子深度z^2的增加而減小,這種減小是由光譜儀的有限像素和光學分辨率共同決定的。
04
信噪比
信噪比一般定義為信號功率與噪聲功率的比率,噪聲功率用其方差來定義。OCT的主要噪聲來源有:
A,探測器噪聲,主要來自電子元件的熱波動。
B,由于光子到達和探測器檢測的內在方差產生的散粒噪聲。
C,光源的相對強度噪聲 (RIN)。
理想的OCT系統,應該是其探測器和強度噪聲都被最小化掉了,在散粒噪聲域內工作,其性能僅受限于到達探測器的光子數量。
05
OCT的靈敏度
在光學相干斷層掃描 (OCT) 中,靈敏度指系統檢測樣本反射最微弱信號的能力。數值上,靈敏度是使信號達到信噪比 (SNR) 為1時的信號衰減程度,即信號強度等于系統固有噪聲的點。
06
分貝 (dB) 單位的測量
信噪比或靈敏度常用分貝 (dB) 表示。物理量的dB單位對應10log(Pa/Pb)。光學測量中,光功率 (P) 與光電探測器輸出電流 (I) 成正比,但電功率與I2成正比,因此考慮光功率時,OCT的SNR和靈敏度測量用20log(Pa/Pb)。
07
速度
OCT系統的速度取決于到達探測器的光量。速度與系統積累足夠光子的時間直接相關。其他限制因素包括各部件自身參數的限制,例如:基于光譜儀的光譜域OCT系統速度受相機傳感器和電子元件限制。對于掃頻光源傅里葉域OCT,掃頻激光源的速度常是限制因素。盡管SS-OCT常因速度被選擇,近年來相機速度的進步開始縮小這一差距。
-
三維成像
+關注
關注
0文章
35瀏覽量
11108 -
3D圖像
+關注
關注
0文章
38瀏覽量
10742 -
OCT
+關注
關注
2文章
33瀏覽量
3753
發布評論請先 登錄
相關推薦
7 FPGA在醫療掃頻OCT系統中的應用
從原始的人工智能代理到智能機器資料下載

用于SS-OCT的14位數字化儀ADQ14OCT
[保姆級教程] 從原理到應用,超級詳細的MPU6050傳感器整理,看完這一篇就夠了!
![[保姆級教程] <b class='flag-5'>從</b>原<b class='flag-5'>理到</b>應用,超級詳細的MPU6050傳感器整理,看完這一篇就夠了!](https://file.elecfans.com/web1/M00/D9/4E/pIYBAF_1ac2Ac0EEAABDkS1IP1s689.png)
為實時醫學成像應用部署OCT
傳感器選型攻略:從原理到應用
使用800nm OCT光譜儀實現超深OCT成像





 OCT:從原理到關鍵參數
OCT:從原理到關鍵參數












評論