作者：京東保險 王奕龍

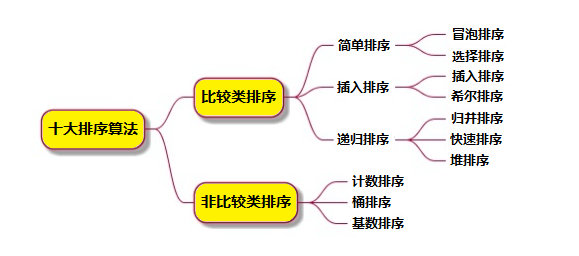
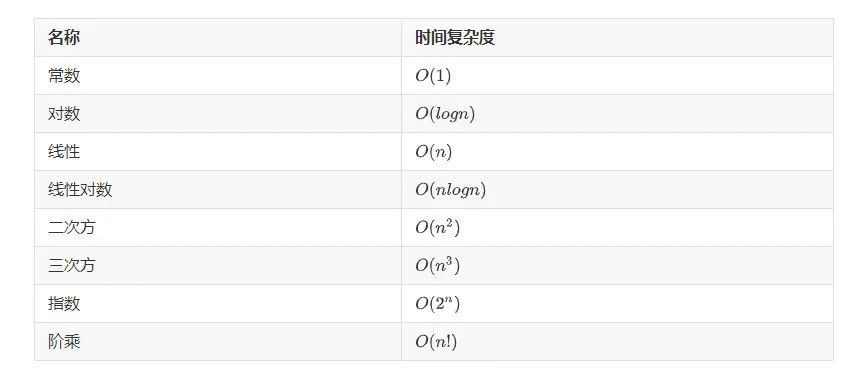
對于小規模數據，我們可以選用時間復雜度為 O(n2) 的排序算法。因為時間復雜度并不代表實際代碼的執行時間，它省去了低階、系數和常數，僅代表的增長趨勢，所以在小規模數據情況下， O(n2) 的排序算法可能會比 O(nlogn) 的排序算法執行效率高。不過隨著數據規模增大， O(nlogn) 的排序算法是不二選擇。本篇我們主要對 O(n2) 的排序算法進行介紹，在介紹之前，我們先了解一下算法特性：

算法特性：

穩定性：經排序后，若等值元素之間的相對位置不變則為穩定排序算法，否則為不穩定排序算法

原地排序：是否借助額外輔助空間

自適應性: 自適應性排序受輸入數據的影響，即最佳/平均/最差時間復雜度不等，而非自適應排序時間復雜度恒定

本篇我們將著重介紹插入排序，選擇排序和冒泡排序了解即可。

插入排序

插入排序的工作方式像 整理手中的撲克牌一樣，即不斷地將每一張牌插入到其他已經有序的牌中適當的位置。

插入排序的當前索引元素左側的所有元素都是有序的：若當前索引為 i，則 [0, i - 1] 區間內的元素始終有序，這種性質被稱為 循環不變式，即在第一次迭代、迭代過程中和迭代結束時，這種性質始終保持不變。

不過，這些有序元素的索引位置暫時不能確定，因為它們可能需要為更小的元素騰出空間而向右移動。插入排序的代碼實現如下：

    private void sort(int[] nums) {
        for (int i = 1; i < nums.length; i++) {
            int base = nums[i];

            int j = i - 1;
            while (j >= 0 && nums[j] > base) {
                nums[j + 1] = nums[j--];
            }
            nums[j + 1] = base;
        }
    }

它的實現邏輯是取未排序區間中的某個元素為基準數 base，將 base 與其左側已排序區間元素依次比較大小，并"插入"到正確位置。插入排序對 部分有序（數組中每個元素距離它的最終位置都不遠或數組中只有幾個元素的位置不正確等情況）的數組排序效率很高。事實上，當逆序很少或數據量不大（n2和nlogn比較接近）時，插入排序可能比其他任何排序算法都要快，這也是一些編程語言的內置排序算法在針對小數據量數據排序時選擇使用插入排序的原因。

算法特性：

空間復雜度：O(1)

原地排序

穩定排序

自適應排序：當數組為升序時，時間復雜度為 O(n)；當數組為降序時，時間復雜度為 O(n2)

希爾排序

插入排序對于大規模亂序數組排序很慢，因為它只會交換相鄰的元素，所以元素只能一步步地從一端移動到另一端，如果最小的元素恰好在數組的最右端，要將它移動到正確的位置需要移動 N - 1 次。

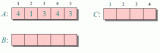
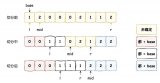
希爾排序是基于插入排序改進的排序算法，它可以交換不相鄰的元素以對數組的局部進行排序，并最終用插入排序將局部有序的數組排序。它的思想是使數組中間隔為 h 的元素有序（h 有序數組），如下圖為間隔為 4 的有序數組：

排序之初 h 較大，這樣我們能將較小的元素盡可能移動到靠近左端的位置，為實現更小的 h 有序創造便利，最后一次循環時 h 為 1，便是我們熟悉的插入排序。這就是希爾排序的過程，代碼實現如下：

    private void sort(int[] nums) {
        int N = nums.length;
        int h = 1;
        while (h < N / 3) {
            h = 3 * h + 1;
        }

        while (h >= 1) {
            for (int i = h; i < N; i++) {
                int base = nums[i];

                int j = i - h;
                while (j >= 0 && nums[j] > base) {
                    nums[j + h] = nums[j];
                    j -= h;
                }
                nums[j + h] = base;
            }

            h /= 3;
        }
    }

希爾排序更高效的原因是它權衡了子數組的規模和有序性，它也可以用于大型數組。排序之初，各個子數組都很短，排序之后子數組都是部分有序的，這兩種情況都很適合插入排序。

選擇排序

選擇排序的實現非常簡單：每次選擇未排序數組中的最小值，將其放到已排序區間的末尾，代碼實現如下：

    private void sort(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            int min = i;
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[j] < nums[min]) {
                    min = j;
                }
            }
            swap(nums, i, min);
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

算法特性：

空間復雜度：O(1)

原地排序

非穩定排序：會改變等值元素之間的相對位置

非自適應排序：最好/平均/最壞時間復雜度均為 O(n2)

冒泡排序

冒泡排序通過 連續地比較與交換相鄰元素實現排序，每輪循環會將未被排序區間內的最大值移動到數組的最右端，這個過程就像是氣泡從底部升到頂部一樣，代碼實現如下：

    public void sort(int[] nums) {
        for (int i = nums.length - 1; i > 0; i--) {
            // 沒有發生元素交換的標志位
            boolean flag = true;
            for (int j = 0; j < i; j++) {
                if (nums[j] > nums[j + 1]) {
                    swap(nums, j, j + 1);
                    flag = false;
                }
            }

            if (flag) {
                break;
            }
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

算法特性：

空間復雜度：O(1)

原地排序

穩定排序

自適應排序：經過優化后最佳時間復雜度為 O(n)

巨人的肩膀

《算法導論 第三版》第 2.1 章

《算法 第四版》第 2.1 章

《Hello 算法》第 11 章

排序算法-希爾排序

審核編輯 黃宇