概要:隨著大數(shù)據(jù)的快速發(fā)展,以概率統(tǒng)計(jì)為基礎(chǔ)的機(jī)器學(xué)習(xí)在近年來受到工業(yè)界和學(xué)術(shù)界的極大關(guān)注,并在視覺、語音、自然語言、生物等領(lǐng)域獲得很多重要的成功應(yīng)用。
摘要
隨著大數(shù)據(jù)的快速發(fā)展,以概率統(tǒng)計(jì)為基礎(chǔ)的機(jī)器學(xué)習(xí)在近年來受到工業(yè)界和學(xué)術(shù)界的極大關(guān)注,并在視覺、語音、自然語言、生物等領(lǐng)域獲得很多重要的成功應(yīng)用,其中貝葉斯方法在過去20多年也得到了快速發(fā)展,成為非常重要的一類機(jī)器學(xué)習(xí)方法.總結(jié)了貝葉斯方法在機(jī)器學(xué)習(xí)中的最新進(jìn)展,具體內(nèi)容包括貝葉斯機(jī)器學(xué)習(xí)的基礎(chǔ)理論與方法、非參數(shù)貝葉斯方法及常用的推理方法、正則化貝葉斯方法等.最后,還針對大規(guī)模貝葉斯學(xué)習(xí)問題進(jìn)行了簡要的介紹和展望,對其發(fā)展趨勢作了總結(jié)和展望。
關(guān)鍵詞
貝葉斯機(jī)器學(xué)習(xí);非參數(shù)方法;正則化方法;大數(shù)據(jù)學(xué)習(xí);大數(shù)據(jù)貝葉斯學(xué)習(xí)
機(jī)器學(xué)習(xí)是人工智能及模式識別領(lǐng)域的共同研究熱點(diǎn),其理論和方法已被廣泛應(yīng)用于解決工程應(yīng)用和科學(xué)領(lǐng)域的復(fù)雜問題.2010年的圖靈獎獲得者為哈佛大學(xué)的LeslieValliant授,其獲獎工作之一是建立了概率近似正確(probably approximate correct,PAC)學(xué)習(xí)理論;2011年的圖靈獎獲得者為加州大學(xué)洛杉磯分校的JudeaPearl教授,其主要貢獻(xiàn)為建立了以概率統(tǒng)計(jì)為理論基礎(chǔ)的人工智能方法,其研究成果促進(jìn)了機(jī)器學(xué)習(xí)的發(fā)展和繁榮。
機(jī)器學(xué)習(xí)的一個重要分支是貝葉斯機(jī)器學(xué)習(xí),貝葉斯方法最早起源于英國數(shù)學(xué)家托馬斯·貝葉斯在1763年所證明的一個關(guān)于貝葉斯定理的一個特例[1-2].經(jīng)過多位統(tǒng)計(jì)學(xué)家的共同努力,貝葉斯統(tǒng)計(jì)在20世紀(jì)50年代之后逐步建立起來,成為統(tǒng)計(jì)學(xué)中一個重要的組成部分[2-3]。貝葉斯定理因?yàn)槠鋵τ诟怕实闹饔^置信程度[4]的獨(dú)特理解而聞名。此后由于貝葉斯統(tǒng)計(jì)在后驗(yàn)推理、參數(shù)估計(jì)、模型檢測、隱變量概率模型等諸多統(tǒng)計(jì)機(jī)器學(xué)習(xí)領(lǐng)域方面有廣泛而深遠(yuǎn)的應(yīng)用[5-6]。從1763年到現(xiàn)在已有250多年的歷史,這期間貝葉斯統(tǒng)計(jì)方法有了長足的進(jìn)步[7]。在21世紀(jì)的今天,各種知識融會貫通,貝葉斯機(jī)器學(xué)習(xí)領(lǐng)域?qū)⒂懈鼜V闊的應(yīng)用場景,將發(fā)揮更大的作用。
1.貝葉斯學(xué)習(xí)基礎(chǔ)
本節(jié)將對貝葉斯統(tǒng)計(jì)方法進(jìn)行簡要的介紹[5]:主要包括貝葉斯定理、貝葉斯模型的推理方法、貝葉斯統(tǒng)計(jì)學(xué)的一些經(jīng)典概念。
1.1貝葉斯定理
用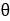 表示概率模型的參數(shù),D表示給定的數(shù)據(jù)集.在給定模型的先驗(yàn)分布和似然函數(shù)
表示概率模型的參數(shù),D表示給定的數(shù)據(jù)集.在給定模型的先驗(yàn)分布和似然函數(shù)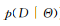 的情況下,模型的后驗(yàn)分布可以由貝葉斯定理(也稱貝葉斯公式)獲得[2]:
的情況下,模型的后驗(yàn)分布可以由貝葉斯定理(也稱貝葉斯公式)獲得[2]:
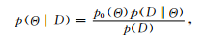 ???(1)
???(1)
其中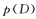 是模型的邊緣似然函數(shù)。
是模型的邊緣似然函數(shù)。
貝葉斯定理已經(jīng)廣為人知,這里介紹一種與貝葉斯公式等價(jià)但很少被人知道的表現(xiàn)形式,即基于優(yōu)化的變分推理:
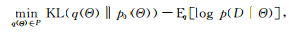 ?? ??(2)
?? ??(2)
其中P為歸一化的概率分布空間。可以證明,式(2)中的變分優(yōu)化的最優(yōu)解等價(jià)于式(1)中的后驗(yàn)推理的結(jié)果[8]。這種變分形式的貝葉斯定理具有兩方面的重要意義:1)它為 變分貝葉斯方法[9](variational Bayes)提供了理論基礎(chǔ);2)提供了一個很好的框架 以便于引用后驗(yàn)約束,豐富貝葉斯模型的靈活性[10]。這兩點(diǎn)在后面的章節(jié)中將具體闡述。
1.2貝葉斯機(jī)器學(xué)習(xí)
貝葉斯方法在機(jī)器學(xué)習(xí)領(lǐng)域有諸多應(yīng)用,從單變量的分類與回歸到多變量的結(jié)構(gòu)化輸出預(yù)測、從有監(jiān)督學(xué)習(xí)到無監(jiān)督及半監(jiān)督學(xué)習(xí)等,貝葉斯方法幾乎用于任何一種學(xué)習(xí)任務(wù).下面簡要介紹較為基礎(chǔ)的共性任務(wù)。
1)預(yù)測。給定訓(xùn)練數(shù)據(jù)D,通過貝葉斯方法得到對未來數(shù)據(jù)x的預(yù)測[5]:
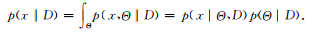 ?? ? ? ? ? ?? (3)
?? ? ? ? ? ?? (3)
需要指出的是,當(dāng)模型給定時(shí),數(shù)據(jù)是來自于獨(dú)立同分布的抽樣,所以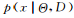 通常簡化為
通常簡化為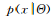 。
。
2)模型選擇。另一種很重要的貝葉斯方法的應(yīng)用是模型選擇[11],它是統(tǒng)計(jì)和機(jī)器學(xué)習(xí)領(lǐng)域一個較為基礎(chǔ)的問題。用M表示一族模型(如線性模型),其中每個元素Θ是一個具體的模型。貝葉斯模型選擇通過比較不同族模型的似然函數(shù)來選取最優(yōu)的:
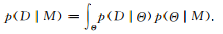 ?? (4)
?? (4)
當(dāng)沒有明顯先驗(yàn)分布的情況下,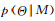 被認(rèn)為是均勻分布.通過式(4)的積分運(yùn)算,貝葉斯模型選擇可以避免過擬合。
被認(rèn)為是均勻分布.通過式(4)的積分運(yùn)算,貝葉斯模型選擇可以避免過擬合。
關(guān)于貝葉斯統(tǒng)計(jì)和貝葉斯學(xué)習(xí)更為詳細(xì)的內(nèi)容,有些論文和教材有更進(jìn)一步的說明]。
2非參數(shù)貝葉斯方法
在經(jīng)典的參數(shù)化模型中模型的參數(shù)個數(shù)是固定的,不會隨著數(shù)據(jù)的變化而變化.以無監(jiān)督的聚類模型為例,如果能通過數(shù)據(jù)本身自動學(xué)習(xí)得到聚類中心的個數(shù),比參數(shù)化模型(如K均值、高斯混合模型等)根據(jù)經(jīng)驗(yàn)設(shè)定一個參數(shù)要好得多;這也是非參數(shù)模型一個較為重要的優(yōu)勢。相比較參數(shù)化貝葉斯方法,非參數(shù)貝葉斯方法(nonparametric Bayesian methods)因?yàn)槠湎闰?yàn)分布的非參數(shù)特性,具有描述數(shù)據(jù)能力強(qiáng)的優(yōu)點(diǎn)[13],非參數(shù)貝葉斯方法因此在2000年以后受到較多關(guān)注[14]。例如具有未知維度的隱式混合模型[15]和隱式特征模型[16]、描述連續(xù)函數(shù)的高斯過程[17]等。需要強(qiáng)調(diào)的是非參數(shù)化貝葉斯方法并不是指模型沒有參數(shù),而是指模型可以具有無窮多個參數(shù),并且參數(shù)的個數(shù)可以隨著數(shù)據(jù)的變化而自適應(yīng)變化,這種特性對于解決大數(shù)據(jù)環(huán)境下的復(fù)雜應(yīng)用問題尤其重要,因?yàn)榇髷?shù)據(jù)的特點(diǎn)之一是動態(tài)多變。下面將主要針對其中的一些較為重要的模型和推理方法進(jìn)行簡要介紹。
2.1狄利克雷過程
狄利克雷過程(Dirichletprocess, DP)是統(tǒng)計(jì)學(xué)家Ferguson于1973年提出的一個定義在概率測度Ω上的隨機(jī)過程[18],其參數(shù)有集中參數(shù)α>0和基底概率分布
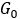 ,通常記為G~
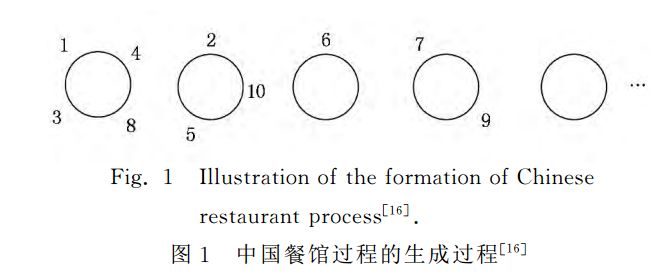
,通常記為G~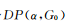 。狄利克雷過程得到的概率分布是離散型的,因此非常適合構(gòu)建混合模型,例如,Antoniak于1974年通過給每個數(shù)據(jù)點(diǎn)增加一個生成概率,構(gòu)造了一個狄利克雷過程混合模型(Dirichlet process mixture, DPM)[15],即???? ? ? ? ?
。狄利克雷過程得到的概率分布是離散型的,因此非常適合構(gòu)建混合模型,例如,Antoniak于1974年通過給每個數(shù)據(jù)點(diǎn)增加一個生成概率,構(gòu)造了一個狄利克雷過程混合模型(Dirichlet process mixture, DPM)[15],即???? ? ? ? ?
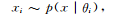 ?(5)
?(5)
其中,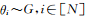 是生成每個數(shù)據(jù)點(diǎn)概率分布的參數(shù),比如高斯分布的均值和協(xié)方差等,N為數(shù)據(jù)點(diǎn)的個數(shù)。
是生成每個數(shù)據(jù)點(diǎn)概率分布的參數(shù),比如高斯分布的均值和協(xié)方差等,N為數(shù)據(jù)點(diǎn)的個數(shù)。
與狄利克雷過程等價(jià)的一個隨機(jī)過程是中國餐館過程(Chinese restaurant process, CRP)[19]。中國餐館過程是定義在實(shí)數(shù)域上的具有聚類特性的一類隨機(jī)過程,也因?yàn)槠涮赜械妮^好展示特性而被經(jīng)常使用。如圖1所示,在中國餐館過程中,假設(shè)有無限張餐桌和若干客人;其中第1名顧客選擇第1張餐桌,之后的顧客按照多項(xiàng)式分布選擇餐桌,其中選擇每張餐桌的概率正比于該餐桌現(xiàn)在所坐的人數(shù),同時(shí)以一定概率(正比于參數(shù)α)選擇一個沒人的餐桌.可以看到,當(dāng)所有的客人選擇完畢餐桌,我們可以按照餐桌來對客人進(jìn)行一個劃分.這里每張餐桌代表一個聚類,每個客人代表一個數(shù)據(jù)點(diǎn)。
可以證明所有的聚類點(diǎn)參數(shù)θ可以通過式(6)得到:
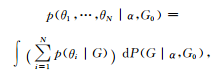 ?(6)
?(6)
將狄利克雷混合模型中的G積分即可得到中國餐館過程,這也說明了兩個隨機(jī)過程的關(guān)系.這種簡潔的表述也很有利于馬爾可夫蒙特卡洛方法的采樣[20]。
另一種構(gòu)造性的狄利克雷過程的表述是截棍過程(stickbreaking construction)[21].具體地說,將一根單位長度的棍,第k次切割都按照剩下的長度按照貝塔分布的隨機(jī)變量,按比例切割:
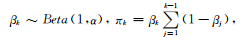 (7)
(7)
即如圖2所示,對于一根長度為單位1的棍,第1次切割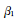 長度,以后每次切割都切割剩下部分
長度,以后每次切割都切割剩下部分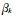 的比例長度。狄利克雷過程的截棍表述是變分推理的基礎(chǔ)[22]。
的比例長度。狄利克雷過程的截棍表述是變分推理的基礎(chǔ)[22]。
2.2印度自助餐過程
與混合模型中每一個數(shù)據(jù)點(diǎn)只屬于一個聚類不同,在特征模型中每一個數(shù)據(jù)點(diǎn)可以擁有多個特征,這些特征構(gòu)成了數(shù)據(jù)生成的過程。這也符合實(shí)際情況中樣本數(shù)據(jù)點(diǎn)有多個屬性的實(shí)際需求。經(jīng)典的特征模型主要有因子分析(factor analysis)、主成分分析(principal component analysis)[24-25]等。在傳統(tǒng)的特征模型中,特征的數(shù)目是確定的,這給模型的性能帶來一定限制.印度自助餐過程(indian buffet process, IBP)是2005年提出的[26],因其非參數(shù)特性能從數(shù)據(jù)中學(xué)習(xí)得到模型中的特征個數(shù),使得模型能夠更好地解釋數(shù)據(jù),已經(jīng)在因子分析、社交網(wǎng)絡(luò)鏈接預(yù)測等重要問題中應(yīng)用[27-29]。
以二值(“0”或“1”)特征為例,假設(shè)有N個數(shù)據(jù)點(diǎn),所有數(shù)據(jù)點(diǎn)的特征向量組成一個特征矩陣,IBP的產(chǎn)生式過程可以形象地類比為N個顧客到一個無窮多個餐品的自助餐館進(jìn)行選餐的過程,用“1”表示選擇,“0”表示不選擇,具體描述如圖3所示的方法進(jìn)行:
1)第1名顧客選擇個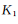 餐品,其中
餐品,其中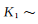
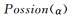 ;
;
2)第2名及以后的顧客有兩種情況:1.對于已經(jīng)被選過的餐品,按照選擇該餐品的人數(shù)成正比的概率選擇該餐品;2.選擇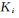 個未被選過的餐品,其中
個未被選過的餐品,其中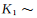
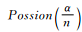 。
。
與中國餐館過程類似,印度自助餐過程也有其對應(yīng)的截棍過程[30].這里不再贅述,僅列出其構(gòu)造性表述如下:
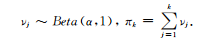 (8)
(8)
但是與中國餐館過程的截棍過程不同的是棍的長度之和并不為1.印度自助餐過程也有其對應(yīng)的采樣方法和變分優(yōu)化求解方法[16,30-31]。
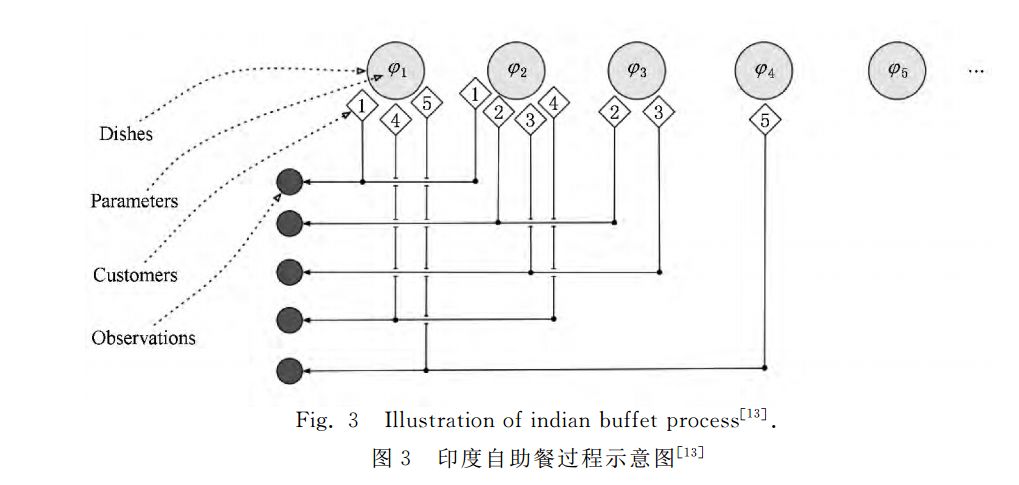
2.3應(yīng)用及擴(kuò)展
貝葉斯方法特別是最近流行的非參數(shù)貝葉斯方法已廣泛應(yīng)用于機(jī)器學(xué)習(xí)的各個領(lǐng)域,并且收到了很好的效果[32]。這里簡要提出幾點(diǎn)應(yīng)用和擴(kuò)展;對于大規(guī)模貝葉斯學(xué)習(xí)的相關(guān)應(yīng)用將在第5節(jié)介紹,也可查閱相關(guān)文獻(xiàn)[13-14,33]。
經(jīng)典的非參數(shù)化貝葉斯方法通常假設(shè)數(shù)據(jù)具有簡單的性質(zhì),如可交換性或者條件獨(dú)立等;但是,現(xiàn)實(shí)世界中的數(shù)據(jù)往往具有不同的結(jié)構(gòu)及依賴關(guān)系。為了適應(yīng)不同的需求,發(fā)展具有各種依賴特性的隨機(jī)過程得到了廣泛關(guān)注。例如,在對文本數(shù)據(jù)進(jìn)行主題挖掘時(shí),數(shù)據(jù)往往來自不同的領(lǐng)域或者類型,我們通常希望所學(xué)習(xí)的主題具有某種層次結(jié)構(gòu),為此,層次狄雷克利過程(hierarchical Dirichlet process, HDP)[34]被提出,可以自動學(xué)習(xí)多層的主題表示,并且自動確定主題的個數(shù).另外,具有多個層次的IBP過程也被提出[35],并用于學(xué)習(xí)深層置信網(wǎng)絡(luò)的結(jié)構(gòu),包括神經(jīng)元的層數(shù)、每層神經(jīng)元的個數(shù)、層間神經(jīng)元的連接結(jié)構(gòu)等。其他的例子還包括具有馬爾可夫動態(tài)依賴關(guān)系的無限隱馬爾可夫模型[36]、具有空間依賴關(guān)系的狄雷克利過程[37]等。
另外,對于有監(jiān)督學(xué)習(xí)問題,非參數(shù)貝葉斯模型最近也受到了廣泛的關(guān)注.例如,社交網(wǎng)絡(luò)數(shù)據(jù)建模和預(yù)測是一個重要的問題,近期提出的基于IBP的非參數(shù)化貝葉斯模型[27,29]可以自動學(xué)習(xí)隱含特征,并且確定特征的個數(shù),取得很好的預(yù)測性能。使用DP混合模型同時(shí)作聚類和分類任務(wù)也取得了很好的結(jié)果[38]。
3貝葉斯模型的推理方法
貝葉斯模型的推理方法是貝葉斯學(xué)習(xí)中重要的一環(huán),推理方法的好壞直接影響模型的性能。具體地說,貝葉斯模型的一個關(guān)鍵性的問題是后驗(yàn)分布通常是不可解的,使得式(3)和式(4)中的貝葉斯積分也是不可解的。這時(shí),就需要一些有效的推理方法。一般而言,主要有兩類方法:變分推理方法(varia-tional inference)和蒙特卡洛方法(Monte Carlo methods)。這兩類方法都在貝葉斯學(xué)習(xí)領(lǐng)域有廣泛的應(yīng)用,下面分別介紹這兩類方法。
3.1變分推理方法
變分法是一種應(yīng)用較廣的近似優(yōu)化方法[39-40],在物理、統(tǒng)計(jì)學(xué)、金融分析、控制科學(xué)領(lǐng)域解決了很多問題。在機(jī)器學(xué)習(xí)領(lǐng)域,變分方法也有較多應(yīng)用:通過變分分析,可以將非優(yōu)化問題轉(zhuǎn)化成優(yōu)化問題求解,也可以通過近似方法對一些較難的問題進(jìn)行變分求解[41]。
在變分貝葉斯方法中,給定數(shù)據(jù)集D和待求解的后驗(yàn)分布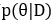 ,變分方法界定其后驗(yàn)分布的近似分布為
,變分方法界定其后驗(yàn)分布的近似分布為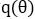 。運(yùn)用杰森不等式,可以得到對數(shù)似然的一個下界(evidence lower bound,ELOB)。
。運(yùn)用杰森不等式,可以得到對數(shù)似然的一個下界(evidence lower bound,ELOB)。
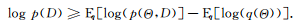 ??(9)
??(9)
通過最大化該對數(shù)似然下界:
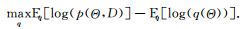 ??(10)
??(10)
或者最小化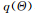 和
和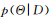 之間的KL散度,就可以完成優(yōu)化求解的過程。因此,變分推理的基本思想是將原問題轉(zhuǎn)化成求解近似分布的優(yōu)化問題,結(jié)合有效的優(yōu)化算法來完成貝葉斯推理的任務(wù)[22,42-43]。
之間的KL散度,就可以完成優(yōu)化求解的過程。因此,變分推理的基本思想是將原問題轉(zhuǎn)化成求解近似分布的優(yōu)化問題,結(jié)合有效的優(yōu)化算法來完成貝葉斯推理的任務(wù)[22,42-43]。
很多時(shí)候,模型Θ中往往有一些參數(shù)θ和隱變量h。這時(shí)變分問題可以通過變分期望最大化方法求解(variational EM algorithm):通過引入平均場假設(shè)(mean-fieldassumption)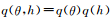 ,可以迭代進(jìn)行EM算法[44]。
,可以迭代進(jìn)行EM算法[44]。
3.2蒙特卡洛方法
蒙特卡洛方法是一類通過利用模擬隨機(jī)數(shù)對未知的概率分布進(jìn)行估計(jì);當(dāng)未知分布很難直接估計(jì)或者搜索空間太大、計(jì)算太復(fù)雜時(shí),蒙特卡洛方法就成為重要的推理和計(jì)算方法[45-46]。例如,貝葉斯機(jī)器學(xué)習(xí)通常需要計(jì)算某個函數(shù)在某種分布(先驗(yàn)或者后驗(yàn))下的期望,而這種計(jì)算通常是沒有解析解的。假設(shè)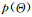 是一個概率分布,目標(biāo)是計(jì)算如下積分:
是一個概率分布,目標(biāo)是計(jì)算如下積分:
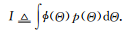 ??(11)
??(11)
蒙特卡洛方法的基本思想是使用如下估計(jì)來近似I:
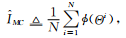 ??(12)
??(12)
其中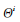 是從P中得到的采樣。根據(jù)大數(shù)定律,在采樣數(shù)目足夠多時(shí),蒙特卡洛方法可以很好地估計(jì)真實(shí)期望。
是從P中得到的采樣。根據(jù)大數(shù)定律,在采樣數(shù)目足夠多時(shí),蒙特卡洛方法可以很好地估計(jì)真實(shí)期望。
上面描述的是蒙特卡洛方法的基本原理,但實(shí)際過程中p的采樣并不是很容易就可以得到,往往采用其他的方法進(jìn)行,常用的方法有重要性采樣(importance sampling)、拒絕采樣(rejection sampling)、馬爾可夫蒙特卡洛方法(Markov Chain Monte Carlo, MCMC)等。前兩者在分布相對簡單時(shí)比較有效,但是對于較高維空間的復(fù)雜分布效果往往不好,面臨著維數(shù)災(zāi)難的問題。下面重點(diǎn)介紹MCMC方法,它在高維空間中也比較有效。
MCMC方法的基本思想是構(gòu)造一個隨機(jī)的馬爾可夫鏈,使得其收斂到指定的概率分布,從而達(dá)到推理的目的[47]。一種較為常用的MCMC方法是Metropolis-Hastings算法[48](MH算法)。在MH算法中,通過構(gòu)造一個從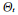 狀態(tài)到
狀態(tài)到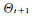 狀態(tài)的轉(zhuǎn)移規(guī)則:
狀態(tài)的轉(zhuǎn)移規(guī)則:
1)根據(jù)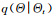 從舊的狀態(tài)采樣中得到一個新的狀態(tài)采樣;
從舊的狀態(tài)采樣中得到一個新的狀態(tài)采樣;
2)計(jì)算接受概率:
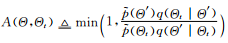 ?(13)
?(13)
3)從0-1均勻分布中采樣得到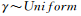 [0, 1]。若
[0, 1]。若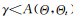 ,則接受采樣
,則接受采樣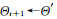 ,否則拒絕采樣
,否則拒絕采樣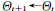 。
。
另一種常用的MCMC方法是吉布斯采樣(Gibbs sampling)[46,49],它是MH算法的一種特例,吉布斯采樣已廣泛應(yīng)用在貝葉斯分析的推理中。吉布斯采用是對多變量分布中每一個變量在其他已經(jīng)觀察得到采樣的變量已知的條件下依次采樣,更新現(xiàn)有的參數(shù),最后收斂得到目標(biāo)后驗(yàn)分布。假設(shè)需要采樣的多元分布為,即每次選出一個維度j:1≤j≤d,其中d是多元分布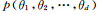 的維度;隨后從條件概率分布
的維度;隨后從條件概率分布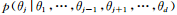 對
對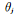 進(jìn)行采樣。
進(jìn)行采樣。
有很多貝葉斯模型都采用了MCMC的方法進(jìn)行推理,取得了很好的效果[20,30,50]。除此之外,還有一類非隨機(jī)游走的MCMC方法———LangevinMCMC[51]和Hybrid MonteCarlo[52]。這一類方法往往有更快的收斂速度,但是表述的復(fù)雜程度較大,因此受歡迎程度不及吉布斯采樣,但是,最近在大數(shù)據(jù)環(huán)境下發(fā)展的基于隨機(jī)梯度的采樣方法非常有效,后文將會簡要介紹。
4正則化貝葉斯理論及應(yīng)用舉例
在第2節(jié)中提到了貝葉斯方法的兩種等價(jià)表現(xiàn)方式,一種是后驗(yàn)推理的方式,另一種是基于變分分析的優(yōu)化方法,其中第2種方式在近年有了較大發(fā)展.基于這種等價(jià)關(guān)系,我們近年來提出了正則化貝葉斯(regularized Bayesian inference, RegBayes)理論[10]:如圖4所示,在經(jīng)典貝葉斯推理過程中,后驗(yàn)分布只能從兩個維度來獲得,即先驗(yàn)分布和似然函數(shù);而在正則化貝葉斯推理中,后驗(yàn)推理轉(zhuǎn)化成一種變分優(yōu)化的方式,通過引入后驗(yàn)正則化,為貝葉斯推理提供了第3維自由度,極大地豐富了貝葉斯模型的靈活性。在RegBayes理論的指導(dǎo)下,我們系統(tǒng)研究了基于最大間隔準(zhǔn)則的判別式貝葉斯學(xué)習(xí)以及結(jié)合領(lǐng)域知識的貝葉斯學(xué)習(xí)等,取得了一系列的成果[]。
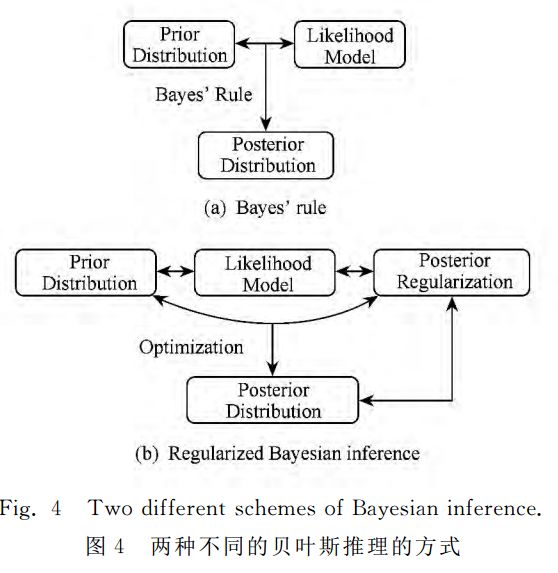
正則化貝葉斯推理的基本框架可以簡述如下,在式(2)的基礎(chǔ)上,引入后驗(yàn)正則化項(xiàng),考慮領(lǐng)域知識或者期望的模型屬性:
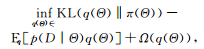 (14)
(14)
其中是一個凸函數(shù)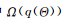 。在運(yùn)用RegBayes解決具體問題時(shí)需要回答下面3個問題:
。在運(yùn)用RegBayes解決具體問題時(shí)需要回答下面3個問題:
問題1.后驗(yàn)正則化從何而來.后驗(yàn)正則化是一個通用的概念,可以涵蓋任何期望影響后驗(yàn)分布的信息。比如,在有監(jiān)督學(xué)習(xí)任務(wù)(如圖像/文本分類)中,我們期望后驗(yàn)分布能夠準(zhǔn)確地預(yù)測,這種情況下我們可以將分類錯誤率(或者某種上界)作為優(yōu)化目標(biāo),通過后驗(yàn)正則化引用到學(xué)習(xí)過程中,典型的例子包括無限支持向量機(jī)[38](infinite SVM)、無限隱式支持向量機(jī)[56](infinitelatent SVM)、最大間隔話題模型[57](maximummargin supervised topic model, MedLDA)等,這些方法均采用了最大間隔原理,在貝葉斯學(xué)習(xí)過程中直接最小化分類錯誤率的上界(即鉸鏈損失函數(shù)),在測試數(shù)據(jù)上取得顯著的性能提升。
另外,在一些學(xué)習(xí)任務(wù)中,一些領(lǐng)域知識(如專家知識或者通過眾包方式收集到的大眾知識)可以提供數(shù)據(jù)之外的一些信息,對提高模型性能有很大幫助。在這種情況下,可以將領(lǐng)域知識作為后驗(yàn)約束,與數(shù)據(jù)一起加入模型中,實(shí)現(xiàn)高效貝葉斯學(xué)習(xí)。需要指出的是大眾知識往往存在很大的噪音,如何采取有效的策略過濾噪音實(shí)現(xiàn)有效學(xué)習(xí)是問題的關(guān)鍵。在這方面,我們提出了將使用邏輯表達(dá)的領(lǐng)域知識魯棒地引入貝葉斯主題模型,實(shí)現(xiàn)了更優(yōu)秀的模型效果[58]。
問題2.先驗(yàn)分布、似然函數(shù)以及后驗(yàn)正則化之間有何關(guān)系。先驗(yàn)分布是與數(shù)據(jù)無關(guān)的,基于先驗(yàn)知識的概率分布不能反映數(shù)據(jù)的統(tǒng)計(jì)特性;似然函數(shù)則是基于數(shù)據(jù)產(chǎn)生的概率分布,反映了數(shù)據(jù)的基本性質(zhì),通常定義為具有良好解析形式的歸一化的概率分布。而后驗(yàn)正則化項(xiàng)同樣是利用數(shù)據(jù)的特性來定義的,但是,它具有更廣泛靈活的方式,不受歸一化的約束,因此,可以更方便準(zhǔn)確地刻畫問題的屬性或者領(lǐng)域知識,如問題1中所舉的最大間隔學(xué)習(xí)以及領(lǐng)域知識與貝葉斯統(tǒng)計(jì)相結(jié)合等示例。甚至可以證明,一些后驗(yàn)分布不可以通過貝葉斯定理得到,但是可以通過后驗(yàn)正則化得到[10]。因此,RegBayes是比經(jīng)典貝葉斯方法更靈活更強(qiáng)大的方法。
問題3.如何求解優(yōu)化問題。雖然正則化貝葉斯具有極強(qiáng)的靈活性,其學(xué)習(xí)算法仍然可以使用變分方法或者蒙特卡洛方法進(jìn)行求解,具體的求解方法請閱讀相關(guān)論文。下面介紹的大數(shù)據(jù)貝葉斯學(xué)習(xí)理論和算法均可以應(yīng)用到快速求解正則化貝葉斯模型[55],這也是目前的研究熱點(diǎn)。
5大數(shù)據(jù)貝葉斯學(xué)習(xí)
隨著互聯(lián)網(wǎng)技術(shù)的發(fā)展,研究面向大數(shù)據(jù)的機(jī)器學(xué)習(xí)理論、算法及應(yīng)用成為當(dāng)前研究的熱點(diǎn)[[59]59],得到學(xué)術(shù)界和工業(yè)界的廣泛關(guān)注。貝葉斯模型有較好的數(shù)據(jù)適應(yīng)性和可擴(kuò)展性,在很多經(jīng)典問題上都取得了很好的效果,但是,傳統(tǒng)貝葉斯模型的一個較大的問題在于其推理方法通常較慢,特別是在大數(shù)據(jù)背景下很難適應(yīng)新的模型的要求。因此,如何進(jìn)行大規(guī)模貝葉斯學(xué)習(xí)方法是學(xué)術(shù)界的重要挑戰(zhàn)之一。可喜的是近期在大數(shù)據(jù)貝葉斯學(xué)習(xí)(big Bayesian learning, BigBayes)方面取得了顯著的進(jìn)展。下面簡單介紹在隨機(jī)算法及分布式算法方面的進(jìn)展,并以我們的部分研究成果作為示例。表1所示為對目前的若干前沿進(jìn)展簡要總結(jié):

5.1隨機(jī)梯度及在線學(xué)習(xí)方法
當(dāng)數(shù)據(jù)量較大時(shí)精確的算法往往耗時(shí)較長,不能滿足需要。一類常用的解決方案是采用隨機(jī)近似算法[60-61]。這類算法通過對大規(guī)模數(shù)據(jù)集的多次隨機(jī)采樣(random subsampling),可以在較快的時(shí)間內(nèi)收斂到較好的結(jié)果。這種思想已經(jīng)在變分推理和蒙特卡洛算法中廣泛采用,簡要介紹如下。
在變分推理方面,如前所述,其核心是求解優(yōu)化問題,因此,基于多次隨機(jī)降采樣的隨機(jī)梯度下降算法成為很自然的選擇。具體地說,隨機(jī)梯度下降算法(stochastic gradient descent, SGD)[62]每次隨機(jī)選取一個數(shù)據(jù)子集,并用該子集上計(jì)算的梯度估計(jì)整個數(shù)據(jù)集上的梯度,對要求解的參數(shù)進(jìn)行更新:
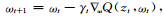 ?(15)
?(15)
其中Q是待優(yōu)化的目標(biāo)函數(shù),是數(shù)據(jù)的第t個子集。值得注意的是,歐氏空間中的梯度并非最優(yōu)的求解變分分布的方向;對于概率分布的尋優(yōu),自然梯度往往取得更快的收斂速度[63]。近期的主要進(jìn)展包括隨機(jī)變分貝葉斯方法[61]以及多種利用模型特性的快速改進(jìn)算法[64][64]。
在蒙特卡洛算法方面,可以將隨機(jī)梯度的方法用于改進(jìn)對應(yīng)的基于梯度的采樣算法,如隨機(jī)梯度朗之萬動力學(xué)采樣方法(stochastic gradient langevin dynamics, SGLD)[65]、隨機(jī)梯度哈密爾頓蒙特卡洛(stochasticHamiltonian Monte Carlo, SHM)[66][66]。這些算法加快了蒙特卡洛采樣的速度、有較好的效果。
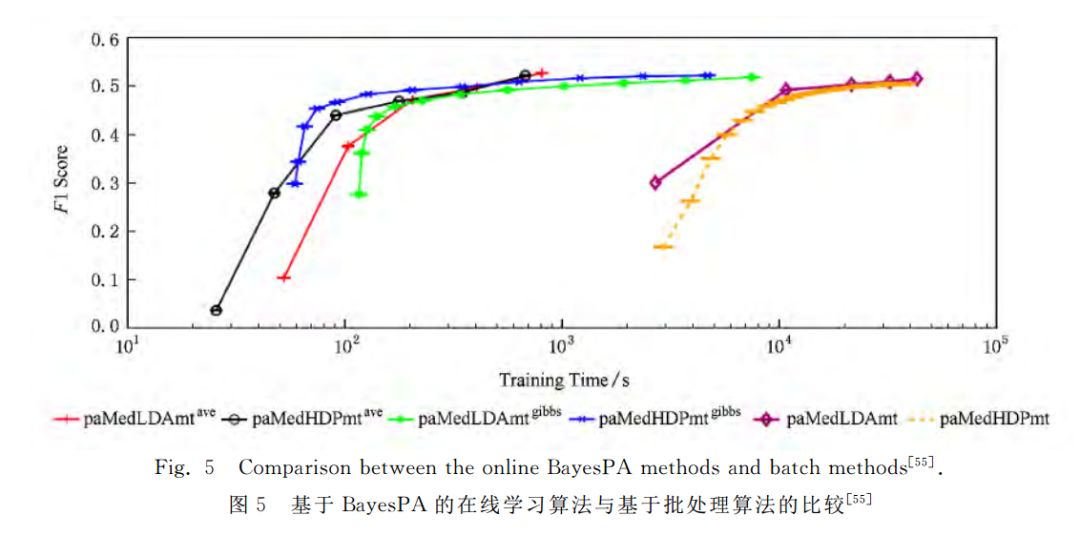
例1.為了適應(yīng)動態(tài)流數(shù)據(jù)的處理需求,基于在線學(xué)習(xí)的大規(guī)模貝葉斯推理算法也成為近期的研究熱點(diǎn),主要工作包括流數(shù)據(jù)變分貝葉斯[67]等。我們近期提出了在線貝葉斯最大間隔學(xué)習(xí)(online Bayesian passive-aggressive learning, Online BayesPA)框架,顯著提高了正則化貝葉斯的學(xué)習(xí)效率,并且給出了在線學(xué)習(xí)后悔值的理論界[55]。在100多萬的維基百科頁面數(shù)據(jù)上的部分實(shí)驗(yàn)結(jié)果如圖5所示,可以看出,基于在線學(xué)習(xí)的算法比批處理算法快100倍左右,并且不損失分類的準(zhǔn)確率。
5.2分布式推理算法
另一種適用于大規(guī)模貝葉斯學(xué)習(xí)問題的算法是基于分布式計(jì)算的[68],即部署在分布式系統(tǒng)上的貝葉斯推理算法。這類算法需要仔細(xì)考慮算法的實(shí)際應(yīng)用場景,綜合考量算法計(jì)算和通信的開銷,設(shè)計(jì)適合于不同分布式系統(tǒng)的推理算法。
一些算法中的部分參數(shù)之間不需要交換信息,只需要計(jì)算得到最后結(jié)果匯總即可;對于這類問題,只需要對原算法進(jìn)行適當(dāng)優(yōu)化,部署在系統(tǒng)上即可有較好的效果。但是,還有更多算法本身并不適合并行化處理,這就意味著算法本身需要修改,使得其可以進(jìn)行分布式計(jì)算,這也是大規(guī)模貝葉斯學(xué)習(xí)的研究熱點(diǎn)之一,并且已經(jīng)取得很多重要進(jìn)展,包括分布式變分推理[67]和分布式蒙特卡洛方法[69]等。
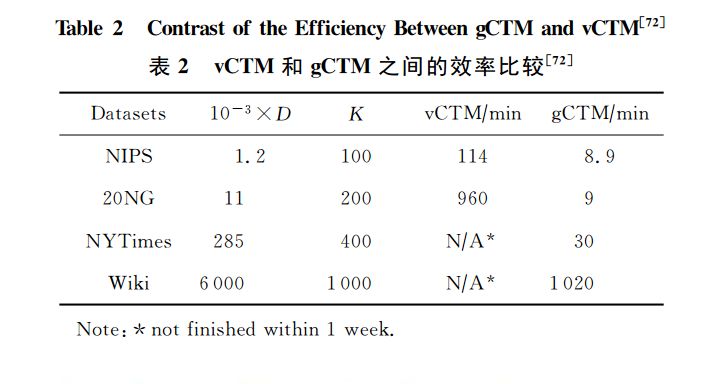
例2.以主題模型為例,經(jīng)典的模型使用共軛狄利克雷先驗(yàn),可以學(xué)習(xí)大規(guī)模的主題結(jié)構(gòu)[70],但是,不能學(xué)習(xí)主題之間的關(guān)聯(lián)關(guān)系。為此,使用非共軛Logistic-Normal先驗(yàn)的關(guān)聯(lián)主題模型(correlated topic model, CTM)[71]被提出。CTM的缺點(diǎn)是其推理算法比較困難,已有的算法只能處理幾十個主題的圖結(jié)構(gòu)學(xué)習(xí)。為此,筆者課題組近期提出了CTM的分布式推理算法[72],可以處理大規(guī)模的數(shù)據(jù)集,學(xué)習(xí)上千個主題之間的圖結(jié)構(gòu)。該算法的部分結(jié)果如表2所示,其中D表示數(shù)據(jù)集大小,K表示主題個數(shù)。由表2可以看出分布式推理算法(即gCTM)極大地提高了模型可以承載的數(shù)據(jù)量(如600萬的維基百科網(wǎng)頁)和更多的主題個數(shù)(如1000)。這個項(xiàng)目的代碼及更多信息已經(jīng)公布,讀者可以自行瀏覽[73]。
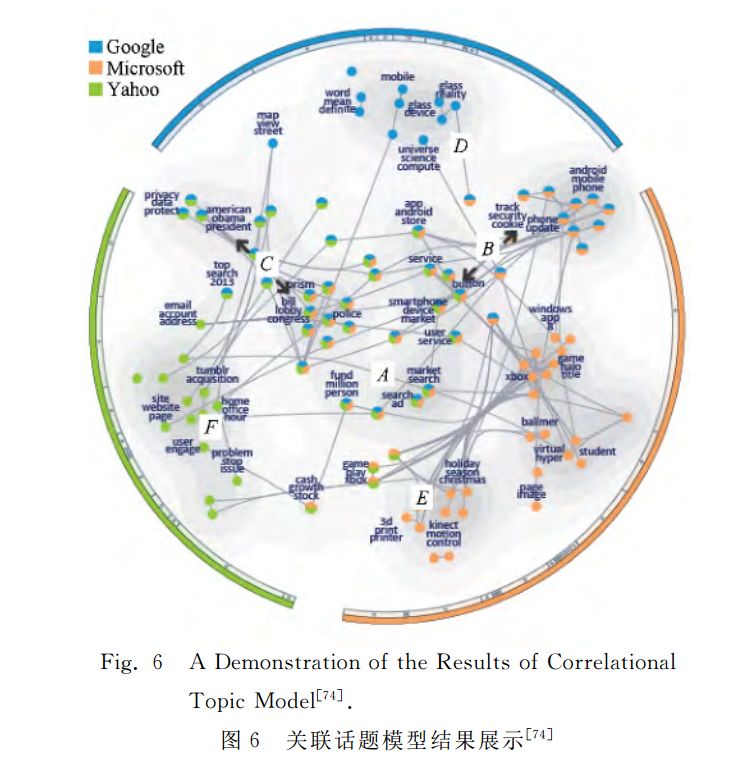
在上述大規(guī)模主題圖結(jié)構(gòu)的學(xué)習(xí)基礎(chǔ)上,進(jìn)一步開發(fā)了“主題全景圖”(TopicPanorama)可視化界面,它可以將多個主題圖結(jié)構(gòu)進(jìn)行融合,并且以用戶友好的方式展現(xiàn)在同一個界面上,如圖6所示,其中每個節(jié)點(diǎn)代表一個主題,節(jié)點(diǎn)之間的邊代表相關(guān)聯(lián)關(guān)系,邊的長度代表關(guān)聯(lián)強(qiáng)度,所用數(shù)據(jù)集為微軟、谷歌、雅虎等3個IT公司相關(guān)的新聞網(wǎng)頁。該可視化工具具有多種交互功能,用戶可以使用放大或縮小功能對主題圖的局部進(jìn)行仔細(xì)查看,同時(shí),也可以修改圖的結(jié)構(gòu)并反饋給后臺算法進(jìn)行在線調(diào)整。多位領(lǐng)域?qū)<乙恢峦庠摴ぞ呖梢苑奖惴治錾缃幻襟w數(shù)據(jù)。更多具體描述參見文獻(xiàn)[74]。
5.3基于硬件的加速
隨著硬件的發(fā)展,使用圖形處理器(graphics processing units, GPU)、現(xiàn)場可編程邏輯門陣列(field-programmablegate array, FPGA)等硬件資源對貝葉斯學(xué)習(xí)方法進(jìn)行加速也是最近興起的研究熱點(diǎn)。例如,有研究者利用GPU技術(shù)對話題模型的變分方法[75]和MCMC算法[76-77]進(jìn)行加速,還有一些研究者利用FPGA對蒙特卡洛算法[78]進(jìn)行加速。利用強(qiáng)大的硬件設(shè)備,搭配適當(dāng)?shù)哪P秃退惴軜?gòu),可以起到事半功倍的效果。
6總結(jié)與展望
貝葉斯統(tǒng)計(jì)方法及其在機(jī)器學(xué)習(xí)領(lǐng)域的應(yīng)用是貝葉斯學(xué)習(xí)的重要研究內(nèi)容。因?yàn)樨惾~斯理論的適應(yīng)性和可擴(kuò)展性使得貝葉斯學(xué)習(xí)得到廣泛的應(yīng)用.非參數(shù)貝葉斯方法和正則化貝葉斯方法極大地發(fā)展了貝葉斯理論,使其擁有更加強(qiáng)大的生命力。
近年來,大數(shù)據(jù)貝葉斯學(xué)習(xí)成為人們關(guān)注的焦點(diǎn),如何加強(qiáng)貝葉斯學(xué)習(xí)的靈活性以及如何加快貝葉斯學(xué)習(xí)的推理過程,使其更加適應(yīng)大數(shù)據(jù)時(shí)代的挑戰(zhàn)成為人們考慮的問題。在這一時(shí)期許多新的方法和理論將被提出,貝葉斯學(xué)習(xí)也與其他許多方面的知識相結(jié)合,如并行計(jì)算、數(shù)據(jù)科學(xué)等,產(chǎn)生很多新的成果。可以預(yù)想,貝葉斯學(xué)習(xí)肯定會有更多更新更好的成果,也會在將來有更廣泛的應(yīng)用。




-
貝葉斯
+關(guān)注
關(guān)注
0文章
77瀏覽量
12579 -
機(jī)器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8424瀏覽量
132765 -
大數(shù)據(jù)
+關(guān)注
關(guān)注
64文章
8896瀏覽量
137517
原文標(biāo)題:貝葉斯機(jī)器學(xué)習(xí)前沿進(jìn)展
文章出處:【微信號:AItists,微信公眾號:人工智能學(xué)家】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
風(fēng)光互補(bǔ)技術(shù)原理及最新進(jìn)展
車聯(lián)網(wǎng)技術(shù)的最新進(jìn)展
ITU-T FG IPTV標(biāo)準(zhǔn)化最新進(jìn)展如何?
深度學(xué)習(xí)在預(yù)測和健康管理中的應(yīng)用
VisionFive 2 AOSP最新進(jìn)展即將發(fā)布!
機(jī)器學(xué)習(xí)之樸素貝葉斯應(yīng)用教程

總結(jié)了高性能計(jì)算在2017年取得的新進(jìn)展,以及未來發(fā)展趨勢
機(jī)器學(xué)習(xí)之樸素貝葉斯
工業(yè)機(jī)器人市場的最新進(jìn)展淺析
關(guān)于深度學(xué)習(xí)的最新進(jìn)展
ASML***的最新進(jìn)展





 總結(jié)了貝葉斯方法在機(jī)器學(xué)習(xí)中的最新進(jìn)展以及對學(xué)習(xí)問題的介紹和展望
總結(jié)了貝葉斯方法在機(jī)器學(xué)習(xí)中的最新進(jìn)展以及對學(xué)習(xí)問題的介紹和展望











評論