RC串聯電路的特點：由于有電容存在不能流過直流電流，電阻和電容都對電流存在阻礙作用，其總阻抗由電阻和容抗確定，總阻抗隨頻率變化而變化。RC 串聯有一個轉折頻率：f0=1/2πR1C1當輸入信號頻率大于f0 時，整個 RC 串聯電路總的阻抗基本不變了，其大小等于 R1。

RC串聯電路的暫態過程基本原理

RC電路的特點是充放點過程按指數函數規律進行的。

1． 充電過程

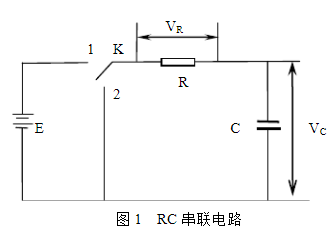
在圖1的電路中，當K扳向“1”的瞬間，電容器尚未積累電荷，此時電動勢E全部 降落在R上最大的充電電流為IO=E/R；隨著電容器電荷的積累，VO增大，R兩端的電壓VR減小，充電電流i跟著減小，著又反過來使VO的增長率變的緩慢；直至VO等于E時，充電過程才終止，電路達到穩定狀態。

在這過程中，電路方程為：

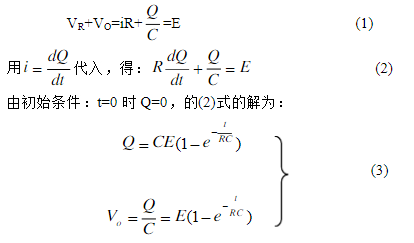
從（3）式可見，Q和VO是隨時間t按指數函數的規律增長的，函數的曲線如圖2（a）所示。

相應可得：

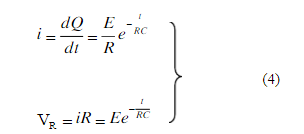
式（4）表明，充電電流i和電阻電壓VR是隨著時間t按指數規律衰減的；起函數曲線

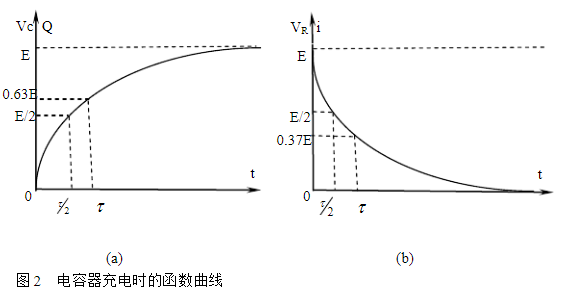
如圖2（b）所示。

2． 放電過程

在圖1的電路中，當電容器C充電后（VO=EK），把開關由“1”扳向“2”，此時電容上C上的電荷就逐漸通過R放電。當開關剛扳向“2”一瞬間，全部電壓VO=E作用在R上，最大的放電電流為IO=E/R，隨后VO逐漸減小，放電電流i也隨著減小，這反過來又使VO的減小變的緩慢。在這過程中，電路的方程為：

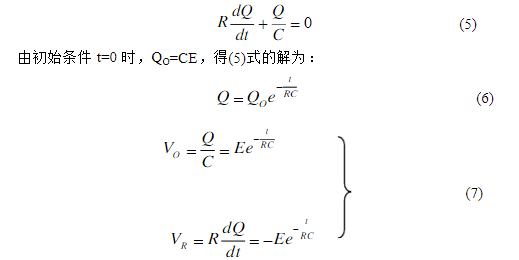
式中VR出現了負號，表示放電電流與充電電流方向相反。

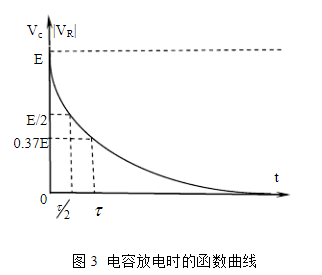
從（6）、（7）兩式可知，Q、VO和|VR|是隨時間t按指數函數規律減小的。其函數曲線如圖3所示。

乘積RC稱為電路的時間常數?。從（6）式可知，當t=?=RC時，電容器上的電荷下降到初始值QO的36.8%。因此，?可作為反映RC電路充放電速度快慢的特征值。

與時間常數?有關的另一個在實驗中比較容易測定的特征量是Q下將（或上升）到QO一半是所需要的時間T1/2，這個時間稱為半衰期，由（3）、（4）式可得：

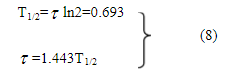
當然，在理論上，t為無窮大時，才有VO=E，i=0。但實際上t=4?~5?時，可近似的認為已充電或放電完畢。從圖2、3中可明顯看到這一點。

若圖1中的開關K在“1”、“2”端迅速來回接通電路時，電容器家體地進行著充電與放電。這個開關的作用可用一個方波來代替，如圖4所示。在上半個周期內，方波電壓+E，

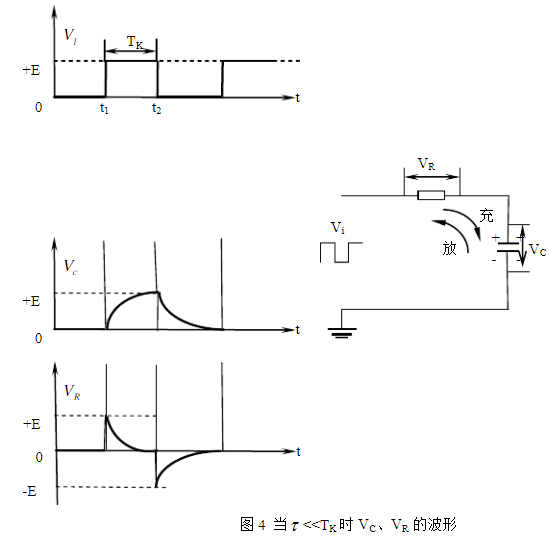
對電容器充電；在下半個周期內，方波電壓為零，電容器放電，顯然方波的作用代替了開關。

若電路的時間常數?《《TK （TK為方波的寬度），在t1時刻，方波從0跳變到E，電容器被充電，在TK的時間內，VO能逐漸增長到E而進入穩態。到了t2時刻，方波從E跳變到0，輸入的兩端相當于短路，于是電容器開始方電，VO從E開始按指數函數規律下降到0而進入另一穩態。

再來看VR，它的波形與充放電電流的波形是一致的。在t1時刻，輸入的方波從0跳變到E，此瞬間方波的跳變全部降落在R上，使VR產生一個同樣大小的跳變，而后隨著VO的生高，VR很快降至零，這樣在R上就形成了一個正的尖脈沖，到了t2時刻，由于電容器放電電流方向相反，所以VR從零跳至一E；同時隨著電容的方電，VR有很快回到零，這樣又形成了一個負的尖脈沖。VR隨t的變化曲線如圖4所示。