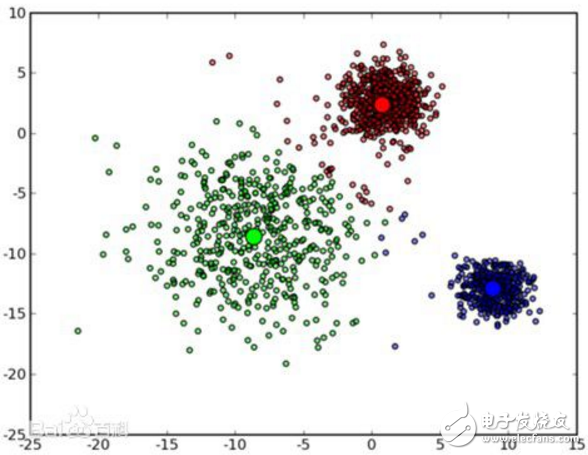
K-means算法是很典型的基于距離的聚類算法，采用距離作為相似性的評價指標，即認為兩個對象的距離越近，其相似度就越大。該算法認為簇是由距離靠近的對象組成的，因此把得到緊湊且獨立的簇作為最終目標。

k個初始類聚類中心點的選取對聚類結果具有較大的影響，因為在該算法第一步中是隨機的選取任意k個對象作為初始聚類的中心，初始地代表一個簇。該算法在每次迭代中對數據集中剩余的每個對象，根據其與各個簇中心的距離將每個對象重新賦給最近的簇。當考察完所有數據對象后，一次迭代運算完成，新的聚類中心被計算出來。如果在一次迭代前后，J的值沒有發生變化，說明算法已經收斂。

算法過程如下：

1）從N個文檔隨機選取K個文檔作為質心

2）對剩余的每個文檔測量其到每個質心的距離，并把它歸到最近的質心的類

3）重新計算已經得到的各個類的質心

4）迭代2～3步直至新的質心與原質心相等或小于指定閾值，算法結束

具體如下：

輸入：k， data［n］;

（1） 選擇k個初始中心點，例如c［0］=data［0］，…c［k-1］=data［k-1］；

（2） 對于data［0］….data［n］，分別與c［0］…c［k-1］比較，假定與c［i］差值最少，就標記為i；

（3） 對于所有標記為i點，重新計算c［i］={ 所有標記為i的data［j］之和}/標記為i的個數；

（4） 重復（2）（3），直到所有c［i］值的變化小于給定閾值。

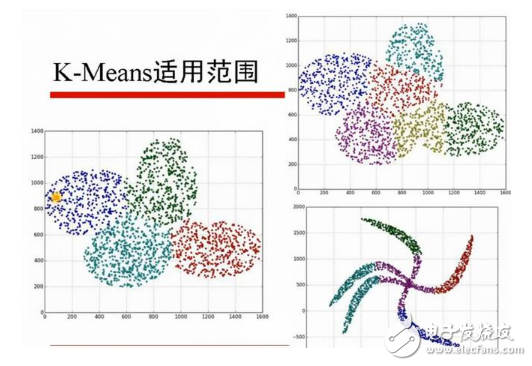
Kmeans算法的優缺點

K-means算法的優點是：首先，算法能根據較少的已知聚類樣本的類別對樹進行剪枝確定部分樣本的分類；其次，為克服少量樣本聚類的不準確性，該算法本身具有優化迭代功能，在已經求得的聚類上再次進行迭代修正剪枝確定部分樣本的聚類，優化了初始監督學習樣本分類不合理的地方；第三，由于只是針對部分小樣本可以降低總的聚類時間復雜度。

K-means算法的缺點是：首先，在 K-means 算法中 K 是事先給定的，這個 K 值的選定是非常難以估計的。很多時候，事先并不知道給定的數據集應該分成多少個類別才最合適；其次，在 K-means 算法中，首先需要根據初始聚類中心來確定一個初始劃分，然后對初始劃分進行優化。這個初始聚類中心的選擇對聚類結果有較大的影響，一旦初始值選擇的不好，可能無法得到有效的聚類結果；最后，該算法需要不斷地進行樣本分類調整，不斷地計算調整后的新的聚類中心，因此當數據量非常大時，算法的時間開銷是非常大的。

K-means算法對于不同的初始值，可能會導致不同結果。解決方法：

1.多設置一些不同的初值，對比最后的運算結果，一直到結果趨于穩定結束

2.很多時候，事先并不知道給定的數據集應該分成多少個類別才最合適。通過類的自動合并和分裂，得到較為合理的類型數目 K，例如 ISODATA 算法。

K-means算法的其他改進算法如下：

1. k-modes 算法：實現對離散數據的快速聚類，保留了k-means算法的效率同時將k-means的應用范圍擴大到離散數據。

2. k-Prototype算法：可以對離散與數值屬性兩種混合的數據進行聚類，在k-prototype中定義了一個對數值與離散屬性都計算的相異性度量標準。

大家接觸的第一個聚類方法，十有八九都是K-means聚類啦。該算法十分容易理解，也很容易實現。其實幾乎所有的機器學習和數據挖掘算法都有其優點和缺點。

（1）對于離群點和孤立點敏感；

（2）k值選擇;

（3）初始聚類中心的選擇；

（4）只能發現球狀簇。

對于這4點呢的原因，讀者可以自行思考下，不難理解。針對上述四個缺點，依次介紹改進措施。

改進1

首先針對（1），對于離群點和孤立點敏感，如何解決？提到過離群點檢測的LOF算法，通過去除離群點后再聚類，可以減少離群點和孤立點對于聚類效果的影響。

改進2

k值的選擇問題，在安徽大學李芳的碩士論文中提到了k-Means算法的k值自適應優化方法。下面將針對該方法進行總結。

首先該算法針對K-means算法的以下主要缺點進行了改進：

1）必須首先給出k（要生成的簇的數目），k值很難選擇。事先并不知道給定的數據應該被分成什么類別才是最優的。

2）初始聚類中心的選擇是K-means的一個問題。

李芳設計的算法思路是這樣的：可以通過在一開始給定一個適合的數值給k，通過一次K-means算法得到一次聚類中心。對于得到的聚類中心，根據得到的k個聚類的距離情況，合并距離最近的類，因此聚類中心數減小，當將其用于下次聚類時，相應的聚類數目也減小了，最終得到合適數目的聚類數。可以通過一個評判值E來確定聚類數得到一個合適的位置停下來，而不繼續合并聚類中心。重復上述循環，直至評判函數收斂為止，最終得到較優聚類數的聚類結果。

改進3

對初始聚類中心的選擇的優化。一句話概括為：選擇批次距離盡可能遠的K個點。具體選擇步驟如下。

首先隨機選擇一個點作為第一個初始類簇中心點，然后選擇距離該點最遠的那個點作為第二個初始類簇中心點，然后再選擇距離前兩個點的最近距離最大的點作為第三個初始類簇的中心點，以此類推，直至選出K個初始類簇中心點。

對于該問題還有個解決方案。之前我也使用過。熟悉weka的同學應該知道weka中的聚類有一個算法叫Canopy算法。

選用層次聚類或者Canopy算法進行初始聚類，然后利用這些類簇的中心點作為KMeans算法初始類簇中心點。該方法對于k值的選擇也是十分有效的。

改進4

只能獲取球狀簇的根本原因在于，距離度量的方式。在李薈嬈的碩士論文K_means聚類方法的改進及其應用中提到了基于2種測度的改進，改進后，可以去發現非負、類橢圓形的數據。但是對于這一改進，個人認為，并沒有很好的解決K-means在這一缺點的問題，如果數據集中有不規則的數據，往往通過基于密度的聚類算法更加適合，比如DESCAN算法。