摘要:
基于Ansys有限元軟件,采用三級子模型技術(shù)對多層銅互連結(jié)構(gòu)芯片進(jìn)行了三維建模。研究了10層銅互連結(jié)構(gòu)總體互連線介電材料的彈性模量和熱膨脹系數(shù)對銅互連結(jié)構(gòu)熱應(yīng)力的影響,在此基礎(chǔ)上對總體互連線介電材料的選擇進(jìn)行優(yōu)化。結(jié)果表明,總體互連線介電材料的熱膨脹系數(shù)對銅互連結(jié)構(gòu)的熱應(yīng)力影響較小,而彈性模量對其影響較大;各層介電材料熱應(yīng)力與彈性模量成正比,SiN界面熱應(yīng)力與彈性模量成反比。最后,為了降低銅互連結(jié)構(gòu)關(guān)鍵位置熱應(yīng)力,通過選用不同參數(shù)材料組合對總體互連線介電材料的選取進(jìn)行優(yōu)化,提高了銅互連結(jié)構(gòu)可靠性。
0引言
隨著集成電路制造技術(shù)進(jìn)入數(shù)十納米級,金屬互連線的寬度不斷減小、層數(shù)不斷增加,更細(xì)更長的金屬互連線的電阻-電容(RC)延遲時間已無法忽略,因此采用銅、低介電常數(shù)(low-k)介電材料代替鋁、二氧化硅來降低RC延遲[1-2]。在多層銅互連結(jié)構(gòu)中,封裝過程中因芯片與基板間的熱膨脹系數(shù)不匹配而產(chǎn)生熱應(yīng)力,直接耦合到low-k介質(zhì)中驅(qū)動界面分層[3],引發(fā)可靠性問題。對low-k介質(zhì)熱應(yīng)力的可靠性研究備受關(guān)注。
目前,國內(nèi)外學(xué)者們的研究內(nèi)容是封裝過程中芯片與基板間的熱膨脹系數(shù)不匹配引發(fā)的互連可靠性,即芯片封裝交互作用[3-11]。X.F.Zhang等人采用了四層銅互連結(jié)構(gòu),通過計算裂紋擴展的能量釋放率研究了介電材料屬性對能量釋放率的影響[3-4]。S.Raghavan等人計算銅互連結(jié)構(gòu)裂紋擴展的能量釋放率,得出能量釋放率最大的位置區(qū)域[5]。C.J.Uchibori等人采用四層銅互連結(jié)構(gòu),使用SiO2分別替代M4層介電材料low-k、SiOC層,能量釋放率降低了34%、35%[6-7]。L.L.Mercado等人通過計算裂紋J積分研究了銅互連結(jié)構(gòu)介電材料、互連層數(shù)對裂紋擴展的影響[8]。L.Lin等人研究了銅柱、焊料、PI開口等尺寸參數(shù)對銅互連結(jié)構(gòu)熱應(yīng)力的影響[9-10]。M.W.Lee等人研究了硅層厚度、基板厚度、PI層厚度、銅柱高度、焊點數(shù)量等對銅互連結(jié)構(gòu)low-k層熱應(yīng)力的影響[11]。
在銅互連結(jié)構(gòu)中,互連級與封裝級的尺寸相差較大,直接對其建模仿真會占用巨大計算資源。采用多級子模型技術(shù)可有效解決這一問題。對于銅互連結(jié)構(gòu),可采用四級子模型技術(shù)進(jìn)行建模[3-4,6-7],但計算精度不高。也可采用二級子模型技術(shù)建模[8-9],但需總體模型精細(xì)網(wǎng)格來保證子模型的計算精度。
本文提出了一種降低銅互連結(jié)構(gòu)關(guān)鍵位置熱應(yīng)力的優(yōu)化方法。綜合考慮計算資源和精度,本文采用三級子模型技術(shù)進(jìn)行結(jié)構(gòu)建模。采用針對10層銅互連結(jié)構(gòu),研究不同的總體互連線介電材料對銅互連結(jié)構(gòu)介電材料熱應(yīng)力的影響。在此基礎(chǔ)上,進(jìn)一步對總體互連線介電材料進(jìn)行優(yōu)化,降低超低介電常數(shù)(ultralow-k,ULK)和SiN界面熱應(yīng)力,最終提高了銅互連結(jié)構(gòu)的可靠性。
1建模與參數(shù)選擇
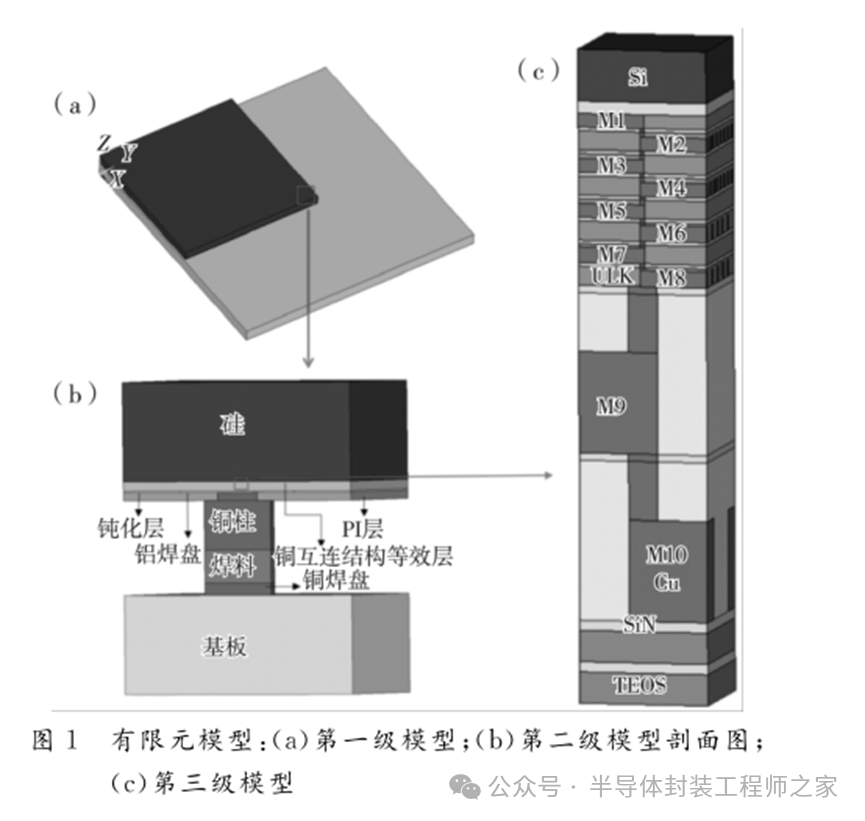
本文使用對稱邊界條件約束對稱模型中心點的所有自由度,禁止產(chǎn)生剛性位移。基于有限元軟件,本文采用三級子模型技術(shù),建立了銅互連結(jié)構(gòu)芯片的三維模型,有限元模型如圖1所示。
考慮到芯片對稱性,采用芯片的1/4結(jié)構(gòu)建模,第一級模型如圖1(a)所示。銅互連結(jié)構(gòu)部分比整個芯片模型的基板和硅層的厚度都薄很多,構(gòu)建第一級模型時采用均勻等效層替代銅互連結(jié)構(gòu),使銅互連結(jié)構(gòu)參與芯片整體模型的形變,該方法的精度不受影響[9-10,12]。第一級模型包括PI層、鈍化層、等效層、銅焊點、基板、硅層等,它們的尺寸如表1所示[13-14]。
第二級模型主要針對關(guān)鍵焊點區(qū)域,其建模區(qū)域源自第一級模型的求解結(jié)果,即熱應(yīng)力值最大區(qū)域,如圖1(b)所示。第二級模型區(qū)域位于距芯片最遠(yuǎn)處的焊點位置,模型邊界條件是將第一級模型計算的位移場通過插值,施加到切割邊界處,切割邊界需遠(yuǎn)離熱應(yīng)力集中區(qū)域。第二級模型包括部分硅、部分基板、銅焊點、PI層、鈍化層,其中銅焊點包括銅柱、焊料、正八邊形鋁焊盤和銅焊盤。采用均勻等效層替代銅互連結(jié)構(gòu)。
第三級模型是是銅互連結(jié)構(gòu)模型,如圖1(c)所示,其包括10層。模型邊界條件是將第二級模型位移場通過插值,施加到切割邊界處。M1~M8層使用ULK作為介電材料。

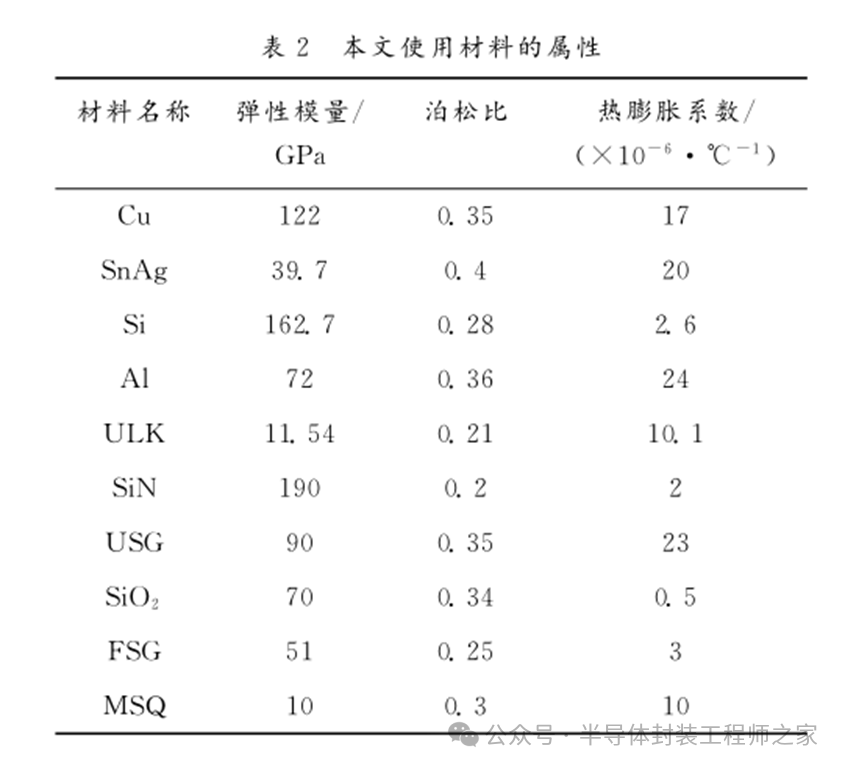
在芯片封裝交互作用研究中,常采用芯片回流焊的溫度作為載荷。雖然回流焊過程中峰值溫度遠(yuǎn)低于制作工藝的峰值溫度,但是,芯片封裝交互作用在low-k界面產(chǎn)生的能量釋放率遠(yuǎn)遠(yuǎn)大于制作工藝產(chǎn)生的能量釋放率,且大于low-k界面的臨界能量釋放率[15]。因此,芯片封裝交互作用會導(dǎo)致銅互連結(jié)構(gòu)low-k界面的斷裂、分層,引發(fā)可靠性問題。將回流焊的溫度作為最高溫度載荷,因填充膠會緩解銅互連結(jié)構(gòu)的熱應(yīng)力,所以本文仿真模型沒有使用填充膠。假設(shè)封裝過程中整體溫度變化均勻,220℃回流焊溫度設(shè)為焊料的熱應(yīng)力自由溫度,溫度以1℃/s的速率降至室溫25℃。本文使用的材料屬性如表2所示[7,10-11,17]。
2結(jié)果分析與討論
本文第一級模型的形變及第二級模型熱應(yīng)力分布圖如圖2所示。

溫度載荷作用后第一級模型Z方向形變?nèi)鐖D2(a)所示。可以看出,封裝芯片的形變呈中間凸起狀,基板邊角部分的形變大于芯片邊角部分。基板邊角承受了最大的形變。原因是,基板的熱膨脹系數(shù)(16×10-6·℃-1~23×10-6·℃-1)比硅大得多,且硅和基板在所有材料中的占比最大,降溫過程中基板收縮的速度比硅快得多,所以引起模型的形變呈凸起狀。
第二級模型等效層Z方向的熱應(yīng)力分布如圖2(b)所示。圖中,紅色部分是拉應(yīng)力,為正值,藍(lán)色部分是壓縮應(yīng)力,為負(fù)值。等效層受拉應(yīng)力的作用區(qū)域大于壓縮應(yīng)力。
第二級模型等效層剪切應(yīng)力分如圖2(c)所示。可以看出,在封裝過程中,等效層同樣受剪切應(yīng)力的影響,但其最大值小于Z方向熱應(yīng)力值。可知,銅互連結(jié)構(gòu)Z方向熱應(yīng)力占據(jù)主導(dǎo)地位。根據(jù)材料力學(xué)最大拉應(yīng)力強度理論,需通過第一主應(yīng)力對銅互連結(jié)構(gòu)進(jìn)行研究。
2.1總體互連線介電材料的彈性模量和熱膨脹系數(shù)對熱應(yīng)力的影響
不同MSQ材料用于總體互連線介電材料時的第一主應(yīng)力分布如圖3所示。采用三級子模型技術(shù)對10層銅互連結(jié)構(gòu)進(jìn)行分析。M1~M8層介電材料使用ULK。M9、M10層為總體互連線,介電材料使用不同的MSQ材料(假設(shè)),材料參數(shù)如表3所示[3]。
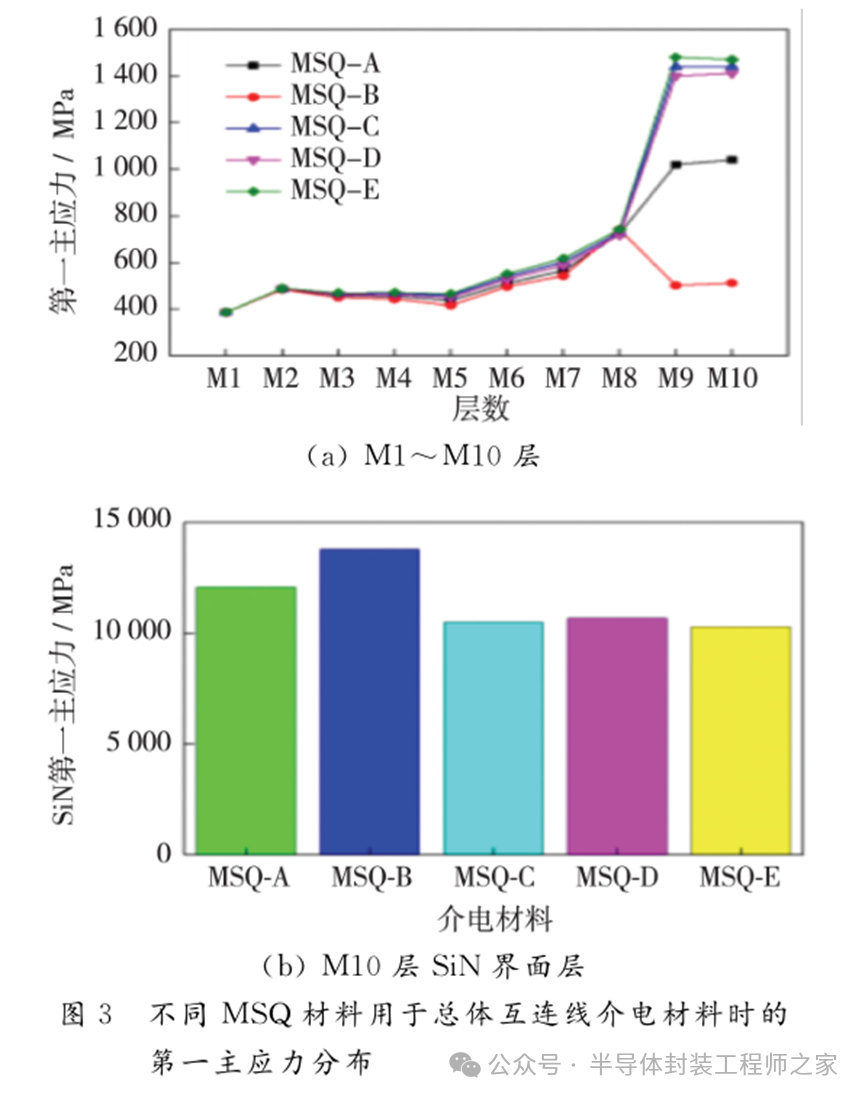
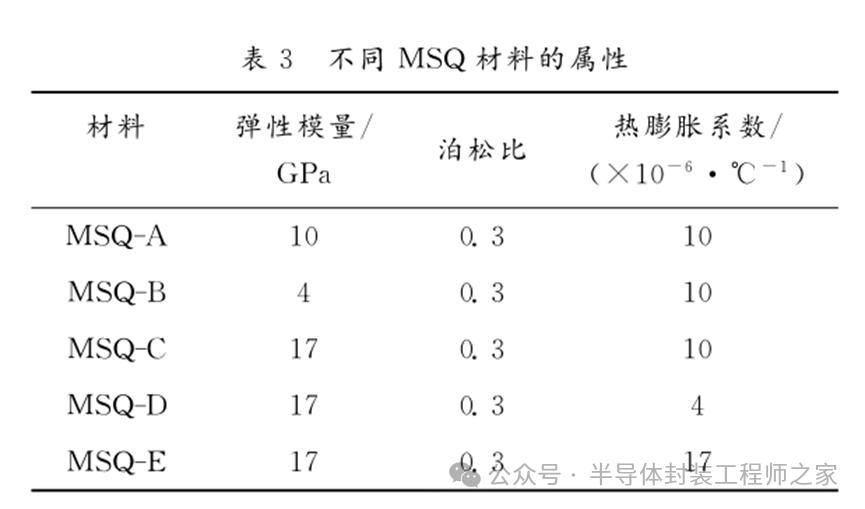
圖3(a)所示為M1~M10層介電材料的熱應(yīng)力分布。可以看出,總體互連線使用不同介電材料時,對M1~M8層使用ULK時,熱應(yīng)力值很小,變化趨勢相同,熱應(yīng)力均在M8層時達(dá)到最大值。原因是,銅焊點的熱應(yīng)力值很大,M8層離銅焊點的距離更近,易產(chǎn)生集中熱應(yīng)力而引發(fā)可靠性問題,M1層的熱應(yīng)力值最小、安全。不同MSQ作總體互連線介電材料時,M9層與M10層的熱應(yīng)力值基本相同,但隨著材料參數(shù)的變化,熱應(yīng)力值整體明顯變化。MSQ材料熱膨脹系數(shù)相同時,彈性模量越小,熱應(yīng)力值越小。如MSQ-B中M9層的熱應(yīng)力值小于M8層,原因是MSQ-B與ULK的彈性模量值相差較大,ULK抵抗形變能力比MSQ-B強,導(dǎo)致ULK熱應(yīng)力較大。MSQ材料彈性模量相同時,隨著熱膨脹系數(shù)的變化,熱應(yīng)力變化并不明顯。可知,M9層、M10層的熱應(yīng)力取決于其彈性模量。
圖3(b)所示為M10層頂部相鄰的SiN界面層的熱應(yīng)力分布。可以看出,MSQ-B作總體互連線介電材料時,SiN界面層的熱應(yīng)力值最大;MSQ材料熱膨脹系數(shù)不變時,SiN界面層熱應(yīng)力與MSQ材料的彈性模量成反比;熱膨脹系數(shù)對SiN界面層的熱應(yīng)力影響較小。SiN界面層的熱應(yīng)力值明顯比M1~M10層大。原因是,MSQ介電材料的彈性模量比SiN界面層小得多,其抗變形能力很弱,導(dǎo)致M10層頂部相鄰的SiN界面層出現(xiàn)熱應(yīng)力集中現(xiàn)象,引起SiN界面分層、斷裂,從而影響銅互連結(jié)構(gòu)的可靠性。
綜上可知,總體互連線介電材料的熱膨脹系數(shù)對M9、M10層和SiN界面層的熱應(yīng)力影響較小,但對彈性模量的影響較大。根據(jù)胡克定理σ=εE(σ、ε表示應(yīng)力和應(yīng)變,E表示彈性模量),溫度載荷下形變?nèi)Q于不同材料的熱膨脹系數(shù)失配,則總體模型形變?nèi)Q于芯片與基板間的熱膨脹系數(shù)失配。銅互連結(jié)構(gòu)在總體模型中占比很小,其對總體模型形變的影響很小,所以總體互連線介電材料的熱膨脹系數(shù)對M9、M10層的熱應(yīng)力影響不大,彈性模量對熱應(yīng)力的影響較大。M9、M10層熱應(yīng)力與總體互連線介電材料的彈性模量成正比,SiN界面層的熱應(yīng)力與彈性模量成反比。
2.2不同的總體互連線介電材料對銅互連結(jié)構(gòu)熱應(yīng)力的影響
通常采用USG、SiO2、FSG等材料作銅互連結(jié)構(gòu)的總體互連線介電材料[7,10,17]。M1~M9層介電材料及SiN界面層的第一主應(yīng)力分布如圖4所示。
USG、SiO2、FSG和MSQ分別作總體互連線介電材料時,M1~M8層(ULK)的熱應(yīng)力分布如圖4(a)所示。可以看出,彈性模量越大,各層熱應(yīng)力值越大,M1層熱應(yīng)力值最小。M1~M2層熱應(yīng)力值迅速增大,之后M2~M5層熱應(yīng)力緩慢變化。原因是,M2層比M1層厚,且M2~M5層厚度相等。從M6層開始,熱應(yīng)力值呈迅速增加的趨勢,M8層熱應(yīng)力達(dá)到最大值。ULK材料的機械特性低、粘附性差,過大熱應(yīng)力引起銅互連結(jié)構(gòu)的分層、斷裂。因此,M8層是易發(fā)生斷裂失效的關(guān)鍵位置之一。
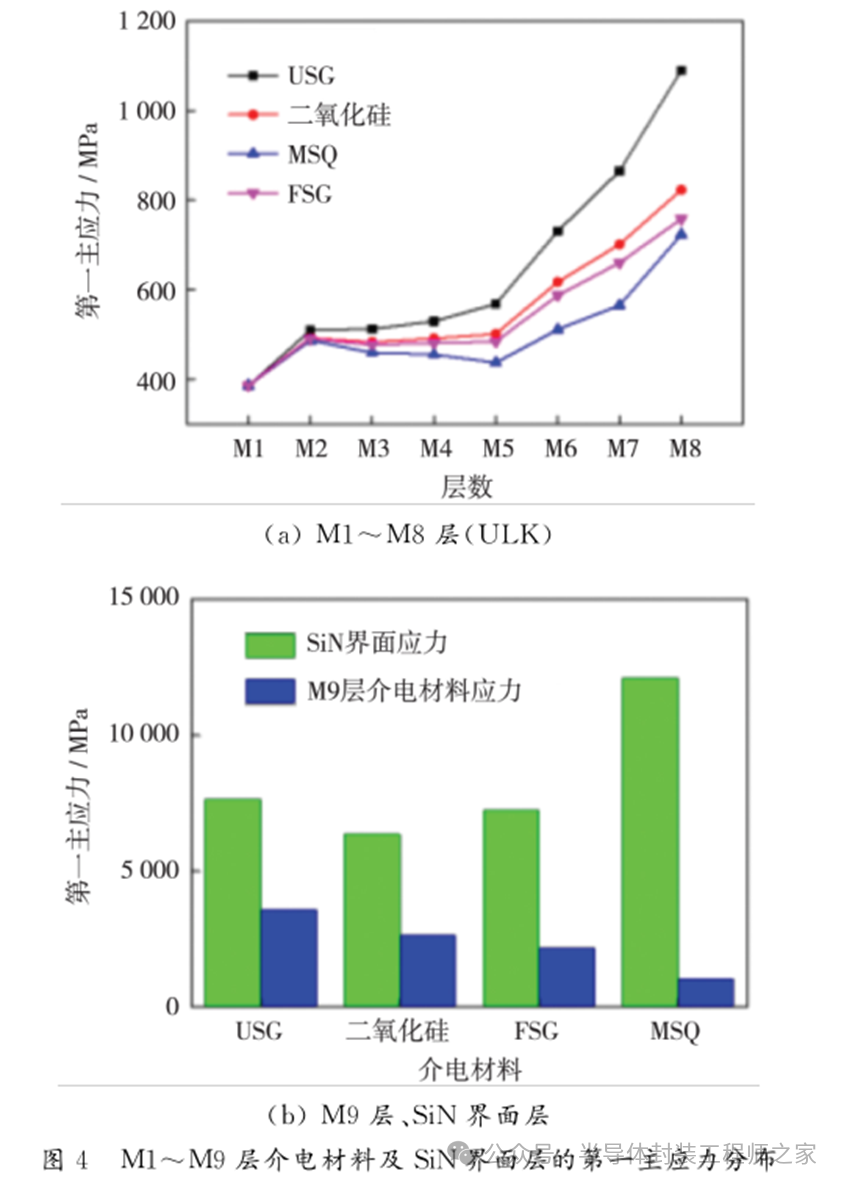
對于不同的總體互連線介電材料,M9層與M10層的熱應(yīng)力值基本相同(從圖3(a)可知),因此圖4(b)只給出了M9層和與M10層相鄰SiN界面層的熱應(yīng)力對比。顯然,與M10相鄰SiN界面層的熱應(yīng)力值遠(yuǎn)大于M9層。可知,與M10相鄰SiN界面層也是易發(fā)生失效的關(guān)鍵位置之一。
從MSQ、FSG到SiO2,它們的彈性模量不斷增大,SiN界面熱應(yīng)力不斷減小。USG介電材料的彈性模量雖最大,但其SiN界面熱應(yīng)力值卻不是最小、略大于SiO2、FSG,這源于USG有較大的熱膨脹系數(shù)而引起的較大熱應(yīng)力。
對于不同的總體互連線介電材料,M9層熱應(yīng)力值從大到小的排序為:USG>SiO2>FSG>MSQ。從圖4(a)可知,M8層熱應(yīng)力從大到小的排序為:USG>SiO2>FSG>MSQ,表明M8層熱應(yīng)力值與M9層熱應(yīng)力密切相關(guān)。為了減小M8層熱應(yīng)力,需使用彈性模量較小的介電材料,但這又使得SiN界面層熱應(yīng)力值較大。因此,需要進(jìn)一步對總體互連線介電材料選取進(jìn)行優(yōu)化。
2.3總體互連線介電材料的選擇優(yōu)化
從上述分析可知,為了提高銅互連結(jié)構(gòu)的可靠性,不僅要減小SiN界面層熱應(yīng)力,還要降低M8層(ULK)熱應(yīng)力值。對這兩類熱應(yīng)力影響最大的是M9層、M10層介電材料的參數(shù)。介電材料及SiN界面層第一主應(yīng)力分布如圖5所示。
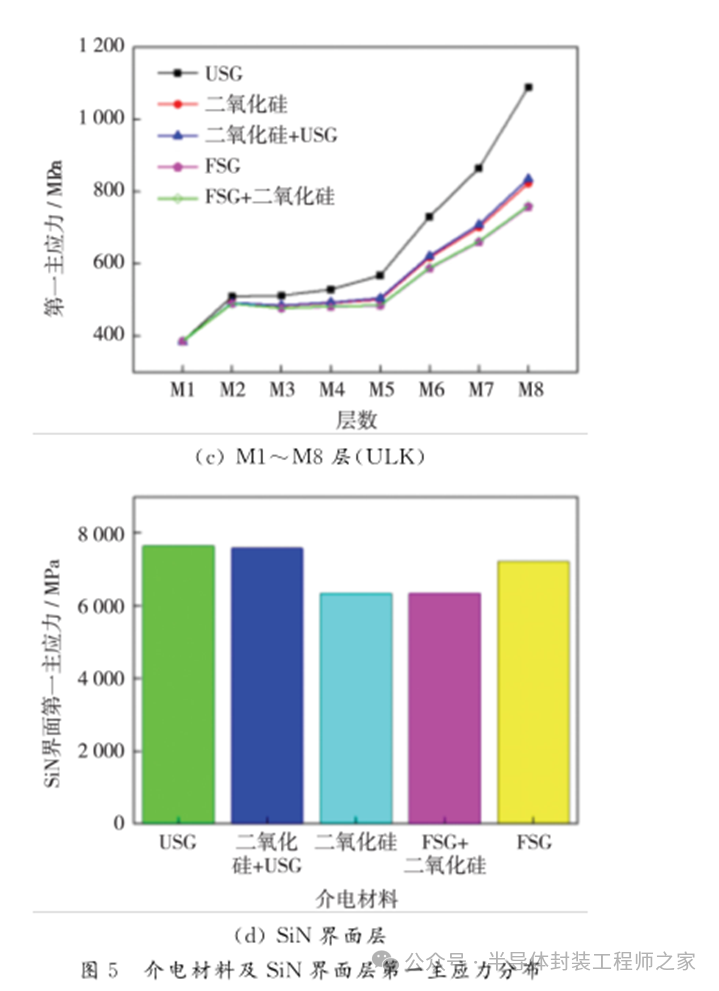
圖中,“USG”表示M9、M10層均使用USG,“SiO2”表示M9、M10層均使用SiO2。“SiO2+USG”表示M9層使用SiO2、M10層使用USG,“FSG+SiO2”表示M9層使用FSG、M10使用SiO2。以此類推。
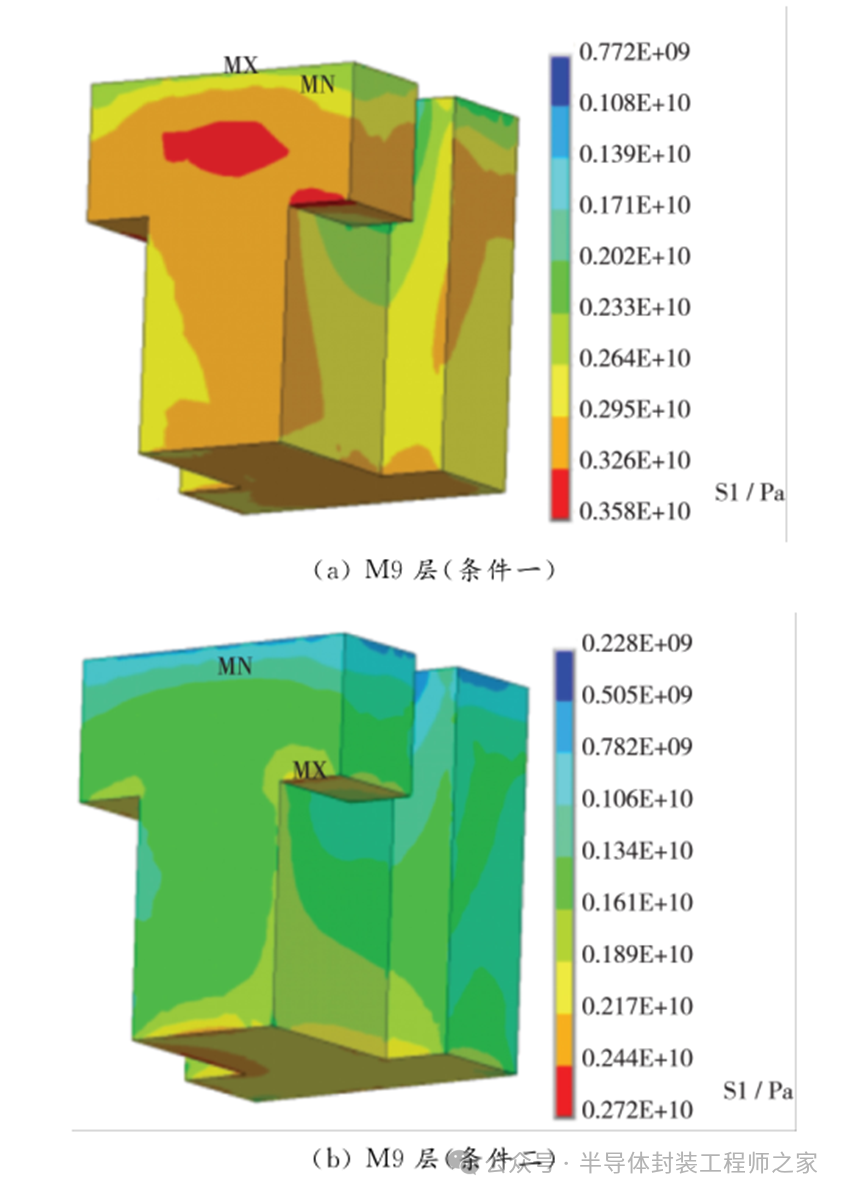
采用“USG”時,M9層(條件一)的熱應(yīng)力分布如圖5(a)所示。可以看出,熱應(yīng)力最大值位于M9層的邊界區(qū)。該區(qū)域與M8層相鄰,造成M8層熱應(yīng)力值增加,易引發(fā)可靠性問題。
采用“SiO2+USG”時,M9層(條件二)的熱應(yīng)力分布如圖5(b)所示。可以看出,M9層熱應(yīng)力值遠(yuǎn)小于圖5(a)的熱應(yīng)力值,最大熱應(yīng)力值位于M9層中間位置,距離M8層較遠(yuǎn),其對M8層熱應(yīng)力的影響降低。這表明,對M9、M10層的優(yōu)化有助于降低關(guān)鍵位置的熱應(yīng)力。
M9、M10層使用不同介電材料組合時,M1~M8層(ULK)熱應(yīng)力分布如圖5(c)所示。可以看出,與采用“USG”相比,采用“SiO2+USG”時熱應(yīng)力值明顯降低,而采用“FSG+SiO2”時熱應(yīng)力值進(jìn)一步降低。采用“SiO2+USG”時,M1~M8層熱應(yīng)力值與采用“SiO2”時熱應(yīng)力值基本相等。采用“FSG+SiO2”時,M1~M8層熱應(yīng)力值與采用“FSG”時熱應(yīng)力值基本相等。這表明,M1~M8層熱應(yīng)力值取決于M9層介電材料,與M10層介電材料關(guān)系不大。M9層選擇彈性模量較小的介電材料時,能有效降低M8層熱應(yīng)力值。
M9、M10層使用不同介電材料組合時,SiN界面層熱應(yīng)力分布如圖5(d)所示。可以看出,采用“SiO2+USG”時,SiN界面層熱應(yīng)力值與采用“USG”時熱應(yīng)力值基本相等;采用“FSG+SiO2”時,SiN界面層熱應(yīng)力值與采用“SiO2”時熱應(yīng)力值基本相等。因此,SiN界面層熱應(yīng)力值與M9層介電材料的關(guān)系不大,取決于M10層介電材料。M9、M10層選擇合適的介電材料,有利于提高銅互連結(jié)構(gòu)的可靠性。采用“FSG+SiO2”時,M8層、SiN界面的熱應(yīng)力值都達(dá)到最小值。
3結(jié)論
基于Ansys有限元分析軟件,以10層銅互連結(jié)構(gòu)為研究對象,采用三級子模型技術(shù)對多層銅互連結(jié)構(gòu)芯片進(jìn)行三維建模。仿真分析了總體互連線介電材料的彈性模量、熱膨脹系數(shù)對銅互連結(jié)構(gòu)熱應(yīng)力的影響。結(jié)果表明,銅互連結(jié)構(gòu)的熱應(yīng)力取決于總體互連線介電材料的彈性模量,而與其熱膨脹系數(shù)關(guān)系不大。為了提高銅互連結(jié)構(gòu)的可靠性,不僅要減小SiN界面層熱應(yīng)力,還要降低M8層(ULK)熱應(yīng)力值。最后,對M9層、M10層的介電材料進(jìn)行優(yōu)化,降低銅互連結(jié)構(gòu)關(guān)鍵位置的熱應(yīng)力,提高器件可靠性。
-
回流焊
+關(guān)注
關(guān)注
14文章
488瀏覽量
17212 -
熱應(yīng)力
+關(guān)注
關(guān)注
0文章
11瀏覽量
10827 -
介電材料
+關(guān)注
關(guān)注
0文章
16瀏覽量
7179
原文標(biāo)題:銅互連結(jié)構(gòu)熱應(yīng)力分析及介電材料選擇優(yōu)化
文章出處:【微信號:深圳市賽姆烯金科技有限公司,微信公眾號:深圳市賽姆烯金科技有限公司】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
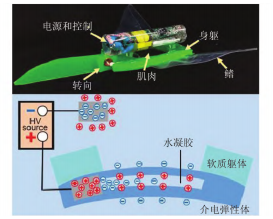
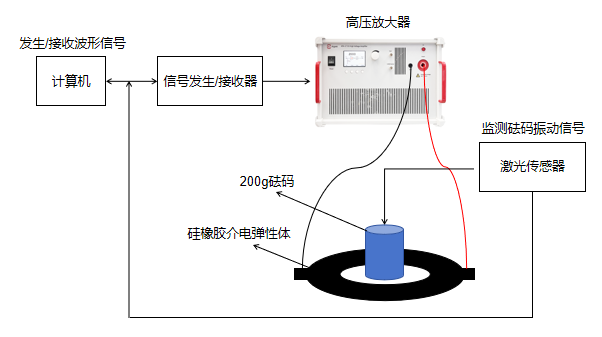
高壓放大器在電致動介電彈性體圓柱驅(qū)動器中的應(yīng)用

佰力博HTS1000高溫介電測試系統(tǒng)特點與測量流程

6種方法去除焊接應(yīng)力
研究透視:芯片-互連材料
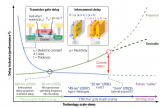
一文了解晶圓級封裝中的垂直互連結(jié)構(gòu)
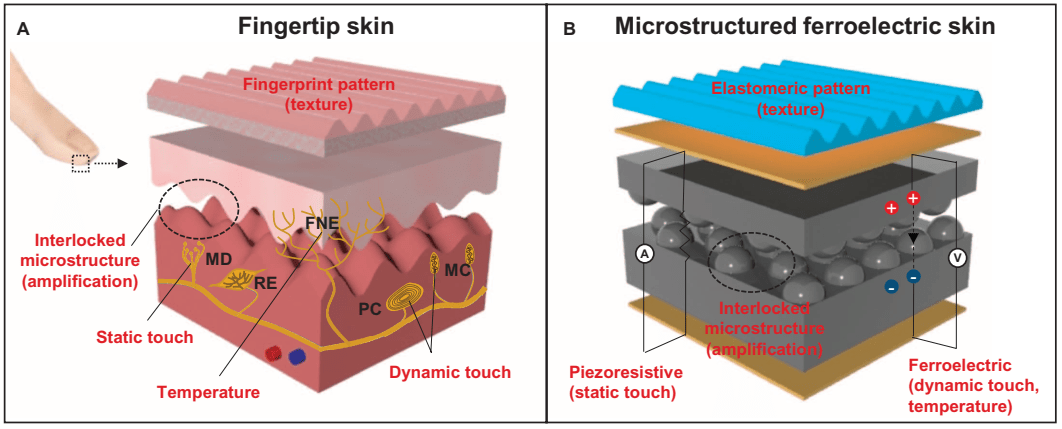
安泰功率放大器在介電材料電子皮膚研究中的應(yīng)用
基于介電電泳的選擇性液滴萃取微流體裝置用于單細(xì)胞分析
機械應(yīng)力和熱應(yīng)力下的BGA焊點可靠性

安泰ATA-7030高壓放大器在介電彈性體智能材料中的應(yīng)用
芯片封裝底部填充材料如何選擇?

安泰功率放大器如何驅(qū)動介電彈性體做運動



















評論