從前面的例子中，可以知道線寬增強因子會讓半導體雷射在動態操作時譜線變寬，接下來我們要討論的是半導體雷射在穩態操作下的發光線寬。

同樣的，假設在一單模操作的雷射中，雷射光在共振腔中沿著z方向行進，我們可以將雷射光的電場表示為：

其中E（t）代表了電場對時間變化較緩慢的包絡，可表示為

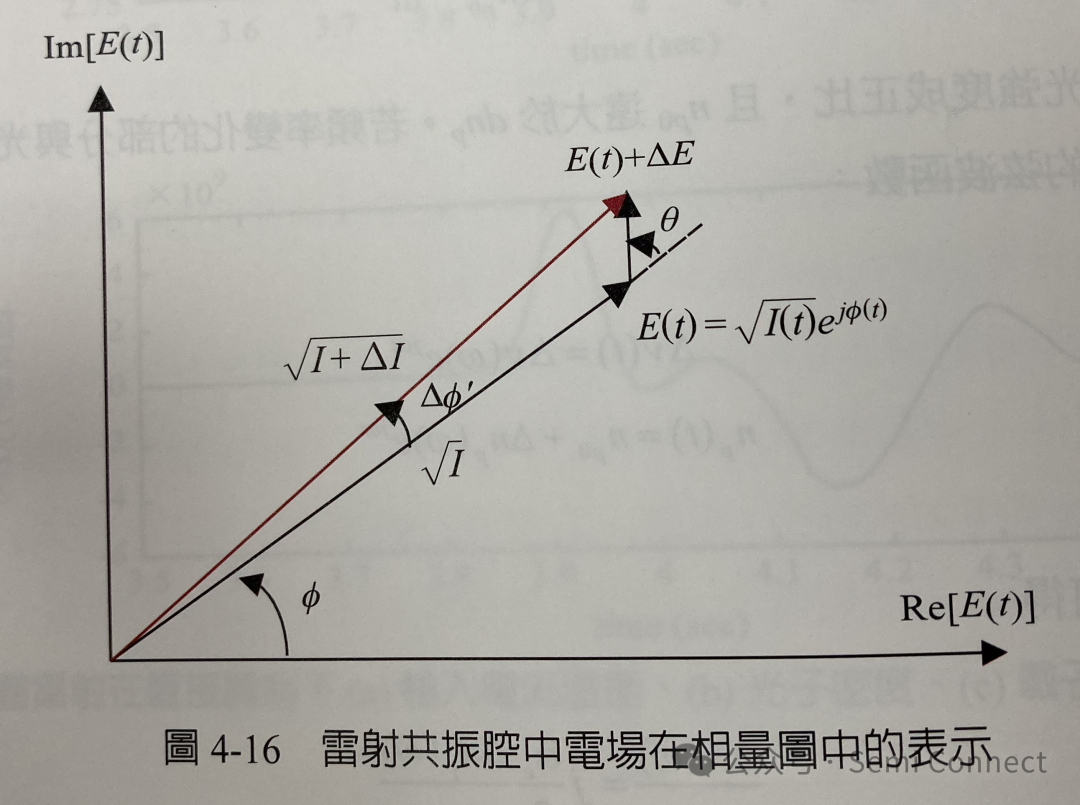
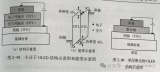
w為雷射光的振蕩角頻率，I（t）是指光場強度和光子數目成正比，我們可以將其正規化并使其代表雷射共振腔內的平均光子數目，而Φ（t）是指此電場包絡的相位，我們可以用相量圖（phasor plot）來表示此電場如圖4-16所示，E（t）以w的角頻率在旋轉。假設有一隨機的自發輻射△E改變了原本E的狀態到E+△E，其中

為方便起見，△E的大小被正規化為1。因此電場的相位被改變了△Φ，而影響△Φ的因素有兩個，表示成

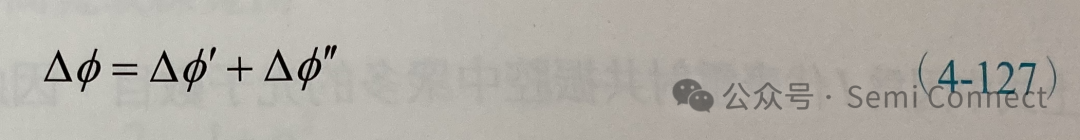
第一個影響△Φ的因素是由于自發輻射△E的加入使得電場相位隨之改變的部分△Φ，這項自發輻射的因素會對所有種類的雷射產生影響，由圖4-16可知

而第二個影響△Φ的因素是光場強度的改變（△I）使得相位發生改變△Φ”，這項因素特別會對半導體雷射產生影響，因為增益和折射率都會受到載子濃度與光場強度變化的影響，因此我們可以使用上式得到：

在這里我們忽略（4-113）式中的負號只取其變化量的大小，相位改變量△Φ可表示為：

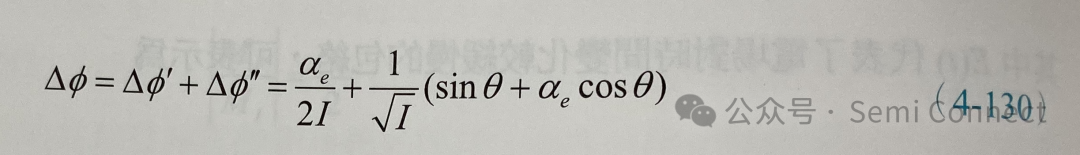
（4-130）式只是一個自發輻射所造成的相位改變量，若將上式在時間t之內對所有的自發輻射積分并取平均值，我們可以得到平均的總相位變化量：

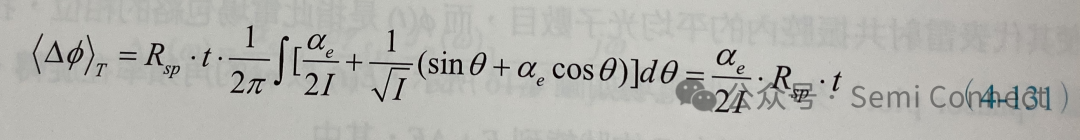
其中Rsp為貢獻到雷射模態的自發輻射速率（因此我們略掉自發放射因子β）。同理：

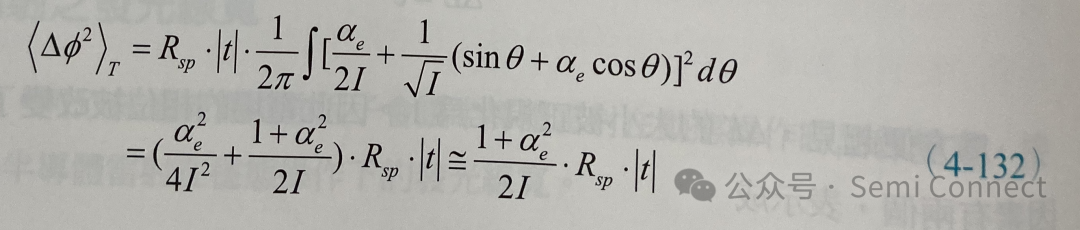
上式中因為I代表雷射共振腔中眾多的光子數目，因此a2e/4I2趨近于零。

接下來要計算雷射發光的強度頻譜以獲取半導體雷射之發光線寬，我們可以將電場相關函數作傅立葉轉換來計算強度頻譜：

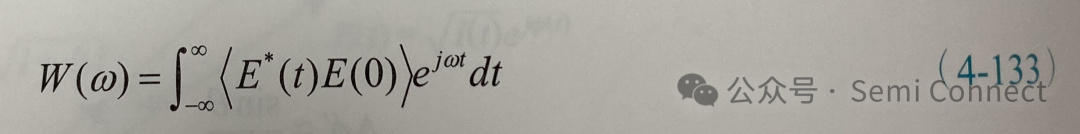
若換成光強度，則上式變為：

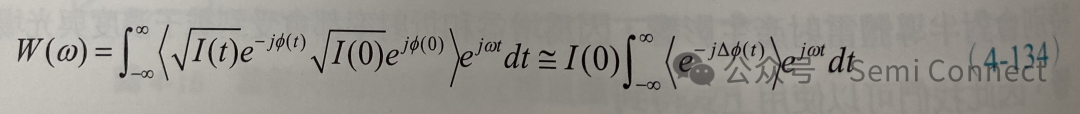
因為自發輻射的事件是隨機發生的，我們可以假設相位變化的機率P（△Φ）是Gaussian形式的機率分布函數，因此：

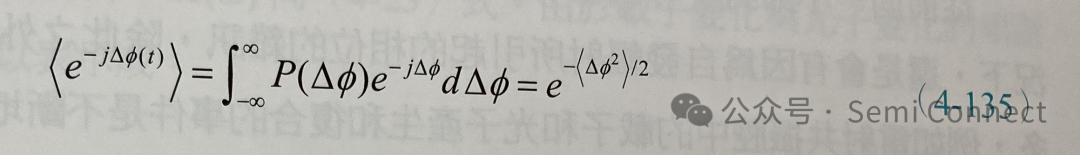
若定義同調（coherent）時間tc為

將上式和（4-132）式比較可知：

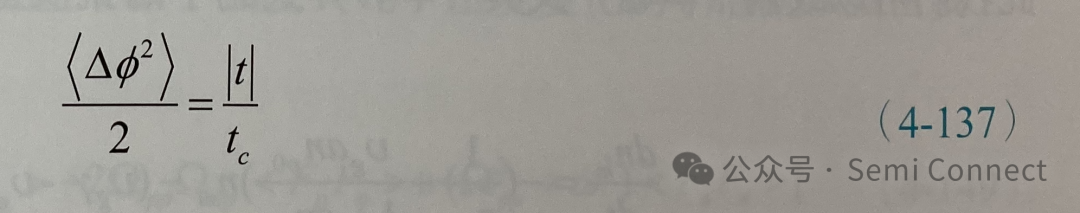
因此，（4-134）式可表示為

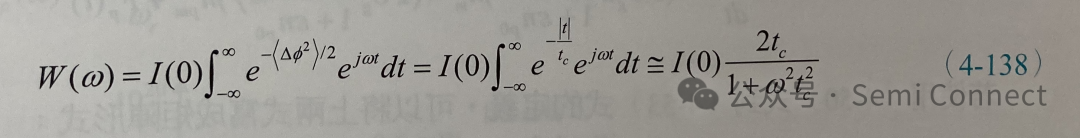
上式為Lorentzian函數的型式，其半高寬或線寬為：

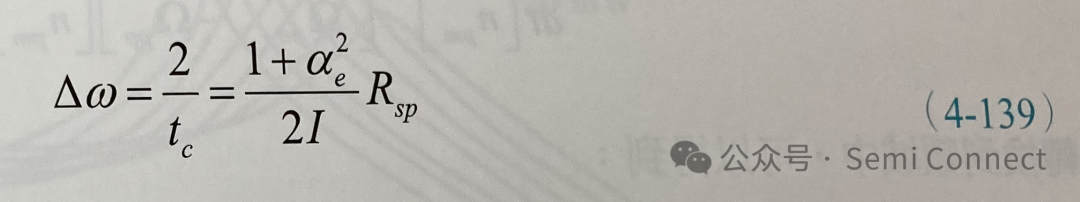
或是

其中Rsp/4兀I為一般雷射線寬的量子極限，被稱為Schawlow-Townes線寬，而在半導體雷射中線寬增強因子使得原本雷射線寬以平方的倍數來增加線寬，這也是ae這個參數的名稱緣由。