一.依據模擬環設計數字環
根據信號與系統的分析理論,一個系統完全由系統函數來確定,因此我們可從系統函數的角度出發,找到模擬電路與數字電路的轉換關系,最終根據環路濾波器的數字域系統函數進行數字化設計。
1.1從模擬到數字——雙線性變換
連續時間系統H(s)的極點有兩種情況:單重節點和多重節點。但是一個多重節點環節可以看成由多個單重極點環節級聯構成。例如,對二重極點的系統,有
H ( s ) = A ( s ? p ) 2 = A s ? p A s ? p H(s)=frac{A}{(s-p)^2}=frac{sqrt{A}}{s-p}frac{sqrt{A}}{s-p}H(s)=(s?p)2A=s?pAs?pA
因此,可以將一階環節
A s ? p = K a s ? p frac{sqrt{A}}{s-p}=frac{K_a}{s-p}s?pA=s?pKa
看成構成H ( s ) H(s)H(s)的最基本環節,其中,K a K_aKa為基本環節的增益。它對應于一階微分方程
d y ( t ) d t ? p y ( t ) = K a x ( t ) frac{dy(t)}{dt}-py(t)=K_ax(t)dtdy(t)?py(t)=Kax(t)
其系統結構如圖1所示。對該系統離散化,主要是對系統中的積分運算離散化。
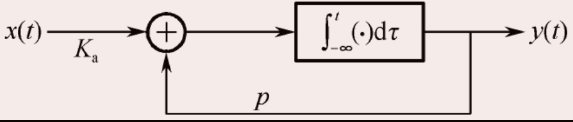
圖 1 圖1圖1
一次積分運算可以用梯形作數值計算,即
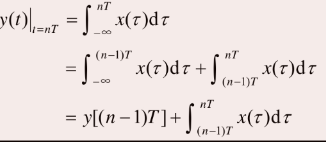
將上式第二行的積分用梯形法近似,則有
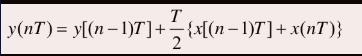
該式為一次積分運算離散化后的數值計算公式,其中的T為采樣間隔。將自變量中的符號T TT隱去,可寫成差分方程的習慣表示形式
y ( n ) = y ( n ? 1 ) + T 2 [ x ( n ? 1 ) + x ( n ) ] y(n)=y(n-1)+frac{T}{2}[x(n-1)+x(n)]y(n)=y(n?1)+2T[x(n?1)+x(n)]
兩邊取單邊z zz變換,并考慮到當y ( n ) = 0 , n < 0 y(n)=0,n<0y(n)=0,n<0有
Y ( z ) = z ? 1 + T 2 [ z ? 1 X ( z ) + X ( z ) ] Y(z)=z^{-1}+frac{T}{2}[z^{-1}X(z)+X(z)]Y(z)=z?1+2T[z?1X(z)+X(z)]
對上式進行整理,得到一階環節的離散系統函數
H 1 ( z ) = Y ( z ) X ( z ) = T 2 1 + z ? 1 1 ? z ? 1 H_1(z)=frac {Y(z)}{X(z)}=frac{T}{2}frac{1+z^{-1}}{1-z^{-1}}H1(z)=X(z)Y(z)=2T1?z?11+z?1
也就是說,一次積分單元離散后,是上式描述的離散系統。
對連續一階系統離散化后,可以得到其系統結構如下圖所示

根據上圖,可求得離散的系統函數為
H i ( z ) = K a H 1 ( z ) 1 ? p H 1 ( z ) H_i(z)=frac{K_a H_1(z)}{1-pH_1(z)}Hi(z)=1?pH1(z)KaH1(z)

將此式與連續的一階環路做對比,得出連續時間系統和離散時間系統之間的轉換公式
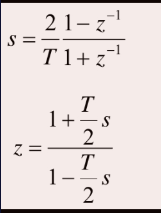
1.2 環路濾波器的數字化
有了系統函數轉換表達式,即可獲得各種模擬環路濾波器所對應的數字化系統函數表達式,進而獲取其數字化實現結構。
對于有源比例環路積分濾波器(理想積分濾波器)來講,其數字化系統函數為
F ( z ) = 1 + s τ 2 s τ 1 = 2 τ 2 + T 2 τ 1 + T τ 1 z ? 1 1 ? z ? 1 F(z)=frac{1+s au_2}{s au_1}=frac{2 au_2+T}{2 au_1}+frac{T}{ au_1}frac{z^{-1}}{1-z^{-1}}F(z)=sτ11+sτ2=2τ12τ2+T+τ1T1?z?1z?1
由于在二階鎖相環路中,理想二階環路具有共他兩種環路無法比擬的優異性能,因此接下來主要討論這種環路濾波器及其構成的鎖相環路。
對于上式,令
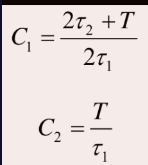
則上式變換為
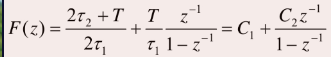
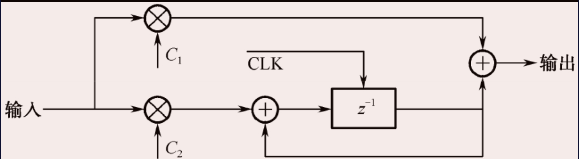
其對應的系統結構可用下圖來表示
1.3 理想二階環的參數設計
各項參數如下:
軟件:Quartus prime 18.0
FPGA系統工作時鐘速率=系統采樣頻率f s f_sfs=8 k H z 8 kHz8kHz
數字震蕩器固有頻率f o = 400 H z f_o=400Hzfo=400Hz
輸入為10bit二進制補碼數據
輸出為10bit二進制補碼數據
鑒相乘法器輸出位寬:19比特
鑒相濾波器系數位寬:8比特
鑒相濾波器輸出數據位寬:30比特
環路增益K=34 Hz
NCO頻率字位寬:30比特
NCO相位字位寬:35比特
為便于比較,我們仍根據一階環實例要求進行設計。根據前面的分析,理想二階環的FPGA實現過程,不過是在一階環的基礎上增加一個環路濾波器功能模塊而已。
quadquad根據前面的推導,求取環路濾波器系數C1、C2的值,需要獲取采樣周期T TT,以及濾波器時間常數τ 1 τ_1τ1、τ 2 τ_2τ2的值。由于系統采樣頻率f s = 8000 H z f_s=8000Hzfs=8000Hz,T = 1 / f s = 1 / 8000 T=1/f_s=1/8000T=1/fs=1/8000s。需要注意的是,τ 1 τ_1τ1、τ 2 τ_2τ2是典型的模擬環路濾波器參數,這也是為什么我們將目前的方法稱為依據模擬環設計數字環的原因。
如何計算τ 1 τ_1τ1、τ 2 τ_2τ2?根據第前面關于環路濾波器的討論,從環路相位裕度參數出發設計這兩個參數,而相位裕度與阻尼系數ξ直接相關。根據圖6-38的仿真結論,一般取阻尼系數ξ=0.7。對于理想二階環來講
ω n = K τ 1 ω_n=sqrt{frac{K}{ au_1}}ωn=τ1K ξ = τ 2 2 K τ 1 ξ=frac{ au_2}{2}sqrt{frac{K}{ au_1}}ξ=2τ2τ1K
注意,在上式中,K KK的單位為r a d / s rad/srad/s,ω n ω_nωn的單位為r a d / s rad/srad/s。現在,我們已經獲取了環路增益參數(K = 34 H z = 213.6283 r a d / s K=34 Hz=213.6283 rad/sK=34Hz=213.6283rad/s)、阻尼系數(ξ = 0.7 ξ=0.7ξ=0.7),還需要獲取一個參數,比如τ 1 、 τ 2 τ_1、τ_2τ1、τ2之間的關系,才能計算出最終的時間常數值,進而計算出C 1 、 C 2 C1、C2C1、C2的值。
quadquad根據模擬環路的性能分析,環路濾波器3 d B 3dB3dB截止帶寬的大小直接影響到V C O VCOVCO輸出的信號質量,要計算出τ 1 、 τ 2 τ_1、τ_2τ1、τ2之間的關系,需要首先確定環路濾波器3dB截止帶寬的f c f_cfc大小。根據前面的分析,取f c = 10 H z f_c=10 Hzfc=10Hz(注意,公式中的截止頻率單位為Hz),則有
10 = 2 2 τ 1 2 ? 2 τ 2 2 10=sqrt{frac{2}{{2}{ au_1^2-2 au_2^2}}}10=2τ12?2τ222
結合前面的公式,帶入K , ξ K,ξK,ξ的值,得到τ 1 , τ 2 au_1, au_2τ1,τ2的值,再根據τ 1 、 τ 2 τ_1、τ_2τ1、τ2的值,分別計算環路濾波器系數C1,C2。
1.4 理想二階環的V e r i l o g H D L Verilog HDLVerilogHDL設計
這里只介紹二階環的環路濾波器的v e r l i o g verliogverliog設計,由前面推導得到的二階鎖相環的Z域公式,將Z域公式轉換到時域中,才能轉換為我們可以用的形式。
F ( z ) = Y ( z ) X ( z ) = C 1 + C 2 z ? 1 1 ? z ? 1 F(z)=frac{Y(z)}{X(z)}=C_1+frac{C_2 z^{-1}}{1-z^{-1}}F(z)=X(z)Y(z)=C1+1?z?1C2z?1
令
C 2 z ? 1 1 ? z ? 1 X ( z ) = D ( z ) frac{C_2 z^{-1}}{1-z^{-1}}X(z)=D(z)1?z?1C2z?1X(z)=D(z)
由z zz變換的性質,上式的時域表達式為:
C 2 x ( n ) + d ( n ) = d ( n + 1 ) C_2x(n)+d(n)=d(n+1)C2x(n)+d(n)=d(n+1)
結合整個Z ZZ域表達式,可得出其最終的時域表達式為:
y ( n ) = C 1 x ( n ) + d ( n ) y(n)=C_1x(n)+d(n)y(n)=C1x(n)+d(n)
具體實現代碼如下:
/* MODULE DECLARATION */ module LoopFilter( rst, clk, pd, frequency_df ); /* FUNCTION DECLARATION */ /* LOCAL PARAMETER */ /* PORT DECLARATION */ input rst; //復位信號,高電平有效 input clk; //FPGA系統時鐘:8 kHz input signed [29:0] pd; // 輸入數據:8 kHz,數據源來自fir濾波器的輸出 output signed [29:0] frequency_df; // 環路濾波器輸出數據 /* REG & WIRE DECLARATION */ reg signed[29:0]sum_d; wire signed[29:0]pd_c2,pd_c1,sum; /ACHIEVEMENT assign pd_c1={{1{pd[29]}},pd[29:1]};//C1 assign pd_c2={{9{pd[29]}},pd[29:9]};//C2 always @(posedge clk or posedge rst) if (rst) sum_d <= 0; else sum_d <= sum; assign sum = pd_c2 + sum_d; assign frequency_df = sum_d + pd_c1; endmodule
這里需要說明的是,為了簡化運算,C1和C2以移位代替了乘法,所以數值采用了近似的方法。
再結合一階環中的其他代碼,就可以得到完整的二階環v e r l i o g verliogverliog代碼。
二.二階環路濾波器仿真相關結論
經過對二階環的仿真,我們得出了下面的結論:
理想二階環路增益直接影響環路的鎖定性能,當環路參數設定后,環路的最大增益就確定了,當增益超過這個值時,環路不能鎖定。
環路能夠正常鎖定的情況下,增益越大,鎖定時間越大,鎖定速度越快。
理想二階環路的捕獲帶寬在工程設計中是有限的。
僅改變環路增益,對捕獲帶寬的影響不大。
-
FPGA
+關注
關注
1630文章
21768瀏覽量
604624 -
鎖相環
+關注
關注
35文章
589瀏覽量
87826
原文標題:數字鎖相環:二階環的FPGA實現
文章出處:【微信號:gh_9d70b445f494,微信公眾號:FPGA設計論壇】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
鎖相環二階廣義積分?
二階鎖相環的EBPSK信號解調分析
數字鎖相環(DPLL),數字鎖相環(DPLL)是什么?
采用二階無源環路濾波器實現三階電荷泵鎖相環的設計




 數字鎖相環:二階環的FPGA實現
數字鎖相環:二階環的FPGA實現










評論