本文主要介紹神經網絡理論研究的物理學思想
神經網絡在當今人工智能研究和應用中發揮著不可替代的作用。它是人類在理解自我(大腦)的過程中產生的副產品,以此副產品,人類希望建造一個機器智能來實現機器文明。這個目標在當下如火如荼的人工智能研究中被無限倍凸顯,甚至被認為是一場新的工業革命到來的標志。
在人類社會前幾次工業革命浪潮中,物理學扮演了十分重要的角色,或者說,這些革命的理論基石在于物理學原理的突破,如熱學、量子力學和相對論。但當今的人工智能革命似乎是經驗科學(啟發式的訣竅,如Transformer)所驅動的,在過去20 年間,尤其是谷歌等互聯網巨頭加入這場浪潮之后,人工神經網絡的架構出現了快速迭代。物理學對神經網絡的研究歷史悠久,最早①可追溯到20 世紀80 年代初霍菲爾德(與辛頓一起獲得2024 年諾貝爾物理學獎)聯想記憶網絡的提出;物理學思想在這之后對人工神經網絡和神經動力學的研究都產生了深遠的影響。著名物理學家戴森有一個說法:“嚴謹理論賦予一個課題以智力的深度和精確。在你能證明一個嚴格理論之前,你不可能全面了解你所關注的概念的意義。”②獲得玻爾茲曼獎的物理學家霍菲爾德也曾在一次訪談中提到,“如果你不能用數學的語言去描述大腦,那你將永遠不知道大腦是怎么工作的。”而鑒于他自身的習慣,“如果一個問題和我熟知的物理毫無聯系,那我將無法取得任何的進展”。所以,在人工智能正在重塑人類社會方方面面的同時,我們有必要去了解物理學的思想如何影響人們對神經網絡乃至自我的認知。
01 從伊辛模型談起
伊辛模型是統計物理的標準模型[1]。它雖然被用來描述格點上(比如二維表面)磁矩的集體行為,但是卻包含了非常豐富的物理圖像(比如相變、自發對稱性破缺、普適性等),更讓人震驚的是,這個模型的物理圖像可以向外擴展到多個似乎毫不相關的學科,如經濟學、神經科學、機器學習等。我們先從物理學專業本科生所熟知的態方程講起:
m= tanh(Jm+ h)
這顯然是個迭代方程,因為變量m出現在方程式等號的兩邊,其中J 描述了自旋之間的相互作用,m表示磁化強度矢量,h則表示外加磁場。注意到,該態方程在沒有外加磁場并且相互作用較弱情況下,有且只有一個平庸解,即所有磁化為零,用物理學語言講叫順磁態。然而,當增大相互作用到一定程度時,順磁態將失去穩定,該方程出現兩個非平庸解(物理上叫鐵磁解,即m=±M)。這個過程叫自發對稱性破缺或連續相變。
這個迭代蘊含了神經網絡的形式。神經網絡的基本屬性可以總結為DNA,即數據(data)、網絡(network)和算法(algorithm),如圖1 所示。你把初始化m0看成輸入數據,每迭代一次將生成一個新的m,這個就是神經網絡的中間隱層表示。然而,奇妙的是,神經網絡把J 也變成可以變化的量,這就意味著這個模型是可以變聰明的(即能處理每一個輸入)。這在傳統物理學里很不可思議,因為模型通常需要大物理學家猜出來。而外場可以等價于神經網絡的偏置(見圖1)。那么如何更新J 呢?你只需要寫下一個目標函數,即這個神經網絡,或者學習中的模型要達到什么樣的目標。比如,實現數據的二分類,你可以輕松地寫下
![]()
這里的a 表示數據輸入-輸出對(x, y)(y 在機器學習叫標簽),而fJ 就是這個被J 參數化的神經網絡(其本質顯然是一個非常復雜的嵌套函數,類似于上面態方程的多次迭代,只不過每次迭代的J都不一樣)。
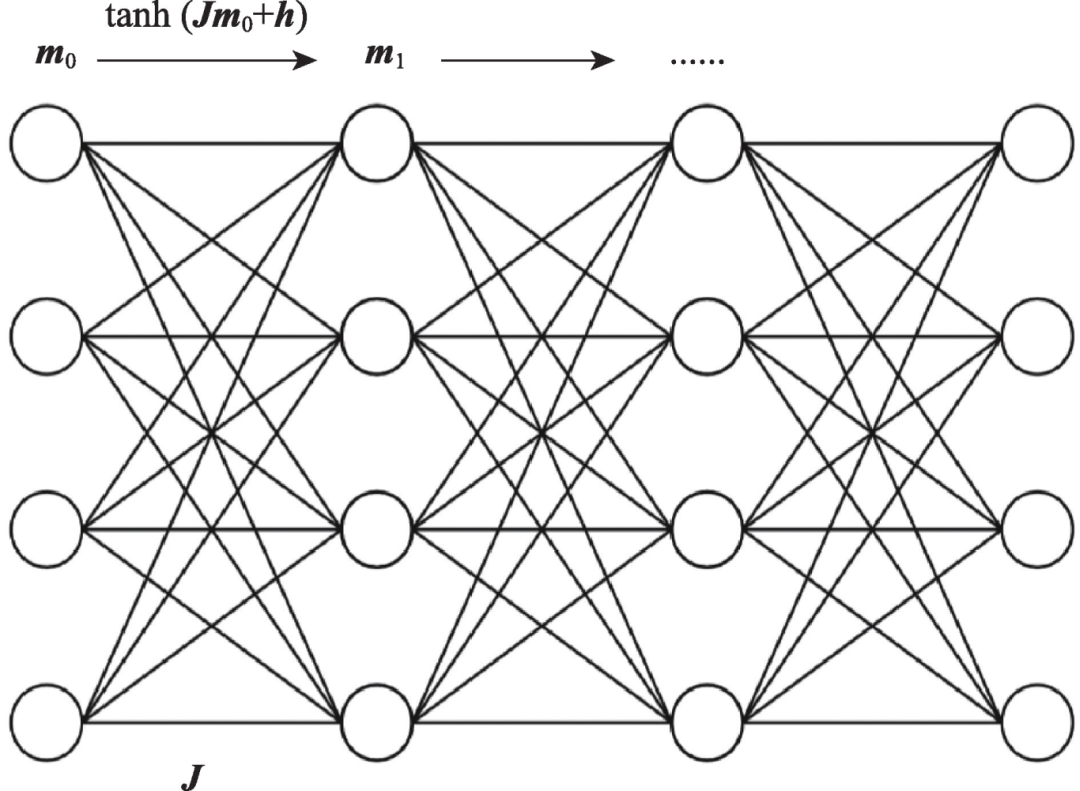
圖1 神經網絡的迭代示意圖
接下來你需要一個算法來驅動這個網絡自我更新。這個算法其實就是梯度下降:dJ/dt= -?JE 。聰明的讀者一眼就認出這是個過阻尼的朗之萬動力學,因為人們在訓練神經網絡時通常在上面的方程右邊加入微弱的白噪聲。所以,神經網絡的學習過程是在你為它定義的勢能函數下的隨機游走(或者布朗運動,見圖2),如果你稍微學過一點隨機動力學的話,你立馬知道這個神經網絡的學習過程存在平衡態,其分布正好是玻爾茲曼分布P(J) = (1/Z))e-E/T ,其中Z 就是統計物理的地標——配分函數,而溫度T 則控制學習過程隨機漲落的程度,類似一個粒子在相同溫度的溶液里運動。此刻,相信你已經獲得足夠深刻的理解:神經網絡的本質是一個從簡單函數(如上述的tanh(),這個函數的形式源自物理上經典自旋有兩個取值并且服從玻爾茲曼正則分布)反復迭代出來的超級復雜并且表達能力超強的函數。這個函數需要不斷更新它的參數,即J 和h,這些參數則構成一個聰明的物理學模型(能自我更新,無需靠大物理學家來定義);而這個模型的更新又是一個布朗運動的過程,服從朗之萬動力學。所以神經網絡的DNA本質在于物理學。
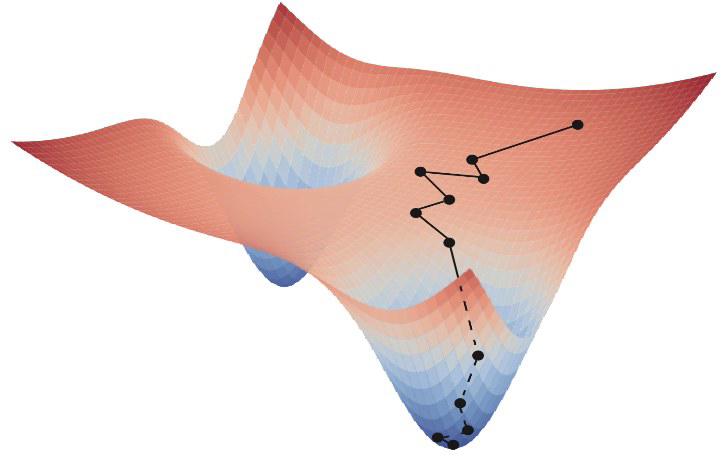
圖2 神經網絡學習過程
02 感知機學習的幾何景觀
接下來首先介紹感知機模型。這個模型當之無愧可稱為人工智能的伊辛模型。它研究的是一群神經元如何實現對輸入數據的分類,這從數學上可以表達為一個不等式 wTx ≥κ ,這里向量w 是神經連接,x 為神經輸入( 例如,機器學習常用的MNIST 數據集中每張手寫體數字為784 維實向量),而κ通常稱為學習的穩定性指標(越大越穩定)。當κ=0,wi=±1 時,我們可以定義這樣的玻爾茲曼統計系綜:
![]()
其中,P代表分類圖片總數,N代表神經連接數目,而Z 則為統計物理學中的配分函數。如果上面的不等式針對每個輸入模式都能滿足的話,則該Z顯然具有構型數(解的數目)的特征,從而可定義自由熵:S=lnZ。這個統計系綜的設計歸功于20 世紀80年代一位杰出的年輕物理學家伊麗莎白·加德納[2],她考慮權重的分布而不是構型從而超越了霍費爾德模型的框架。因為數據的隨機性,求解該熵并非易事,我們這里省去細節(感興趣者可參閱教科書[3])。1989 年,法國物理學家馬克·梅扎爾和他的博士生沃納·克勞斯利用復本方法進行了計算,得出當α = P/N~0.833 時,自由熵消失(意味著該學習問題無解)。這是凝聚態物理理論(自旋玻璃)在計算機和統計學交叉學科的早期典型應用。非常奇妙的是,該結果于今年初被數學家完全嚴格證明[4],而當今高維隨機統計預測在數學里是相當有生命力的一個分支。
該模型自從被提出以來伴隨著不可協調的矛盾,因為長期以來在α《0.833區間,解是存在的,但很多算法找不到它們,或者隨維度升高,算法所能求解的最大α變小。這顯示這個統計推斷問題雖然定義上簡單但從算法復雜度看高度非平庸!這個問題的解釋要等到2013~2014 年間兩篇論文的問世[5]。論文作者的出發點是解空間的幾何結構,類似物理上構型空間的形態或者熵景觀。解決一個難問題通常需要新思路!為了描繪熵景觀,論文作者先從構型空間選取一個典型構型(物理上服從上述玻爾茲曼分布),然后在該構型周圍計數與選定參考構型存在一定漢明距離的構型(或者學習問題的解)。這在物理上等價于自旋玻璃理論的弗蘭之-帕里西勢能。通過復雜推導,作者驚奇地發現,在漢明距離很小的區間,自由熵為負數,哪怕是α非常靠近零。這從物理上意味著,該熵景觀存在大量孤島形態(猶如高爾夫球洞),這也解釋了以往局域算法(如蒙特卡洛)求解的困難性。在松弛不等式的單向性的情況下,數學家近期已經給出了嚴格證明[6,7]。他們在摘要中把這個物理結論稱為Huang-Wong-Kabashima猜想。
一個重要問題的解決通常伴隨新的重要問題的出現,這是科學研究最為迷人的地方。論文[5]在展望中指出了有些特別設計的算法依然可在孤島間找到解,這是跟孤島熵景觀格格不入的。這個新的重要問題看似非常難,但很快就被意大利物理學家理查德·澤奇納及其合作者解決了[8]。這個解決思路也十分巧妙,當然需要很深厚的數學和物理功力。既然自由熵為負,那么可以認為這可能是傳統玻爾茲曼測度的結果,因此把自由熵當成隨機變量,考慮其統計分布并且服從大偏差原理(即P(S)~e-Nr(S) ,其中r(S)稱為率函數)。這么定義之后,理查德·澤奇納等人發現,這個感知器的學習空間居然存在稀有的稠密解團簇!而且,那些高效的經驗算法就是被這些解所吸引的,而完全避開了高爾夫球洞(實際上它們是無法被找到的,掩藏于自由能深谷中)。而這一絕美的物理圖像,同樣于近期被數學家嚴格證明[9]。至此,我們可以總結,雖然感知學習從數學形式上看非常簡潔,但是從物理上可以獲得直觀且非常深刻的見解,并大部分結論能從數學上嚴格證明。從科學上去完全理解一個非平庸的命題應該也必須成為科學文化的一部分,而非一味盲從避開了模型只依賴于數據的現代機器學習方法。
這些研究始于一群喜歡跨學科的物理學家的好奇心,最后卻激起數學家嚴格證明的欲望,讓人們看到高維空間統計推斷的優美。雖然大多物理學家考慮的問題帶有隨機性的成分(比如上述高斯隨機輸入數據),但是,在統計物理學的世界里,存在普適性這個重要的概念,或者說,在某些情況下可以被放心舍棄的細節依然不影響事物的本質。這或許是物理學思想的魅力,也是其他學科的科學家或多或少難以理解之處。這些研究目前已經發展成一個更大的猜想,是否在深度學習乃至大語言模型的解空間里存在大偏差的稀有團簇?這些團簇或許能夠實現舉一反三的邏輯推理能力。
03 無師自通與對稱性破缺
上一個例子講述的是統計物理在理解監督學習的重要作用。接下來我們研究一下無監督學習,即無師自通。無監督學習是讓機器從原始數據中自發地發現隱藏規律,類似人類在嬰兒時期的觀察和學習過程,所以是一種更為重要的認知方式。這個自然界最不可思議的是它的可理解性(愛因斯坦語錄),所以人類可通過模型(幾條合理性的假設)依靠邏輯演繹導出簡潔的物理方程(如牛頓力學、廣義相對論等),從而達到對成千上萬種經驗觀察的高度壓縮。這個與當前大語言模型所做的壓縮即智能有很大的不同③。那么,對于無監督學習,我們如何建模以直擊其本質?
如圖3所示,σ代表輸入原始數據(沒有標簽),ξ1,2代表兩層神經網絡對數據規律的表示,x,y 分別為輸出神經元。無監督學習從數學上可以表達為已知數據推斷連接ξ1,2的過程。為了建立理論模型,我們首先假定存在一個老師網絡,它的連接是完全可知的,因此我們可以通過該老師網絡來生成訓練數據,這個規則叫受限玻爾茲曼機④,圖3 中的i,j,k,l 標示顯層神經元,x, y 是隱層神經元,因此如圖的連接是個伊辛模型,顯層與隱層神經元互為條件獨立,因此便于蒙特卡洛模擬來生成數據。這樣一來,那么具有相同結構的學生網絡能否單從數據悟得老師的連接矩陣呢?這就是一個統計物理可研究的課題。
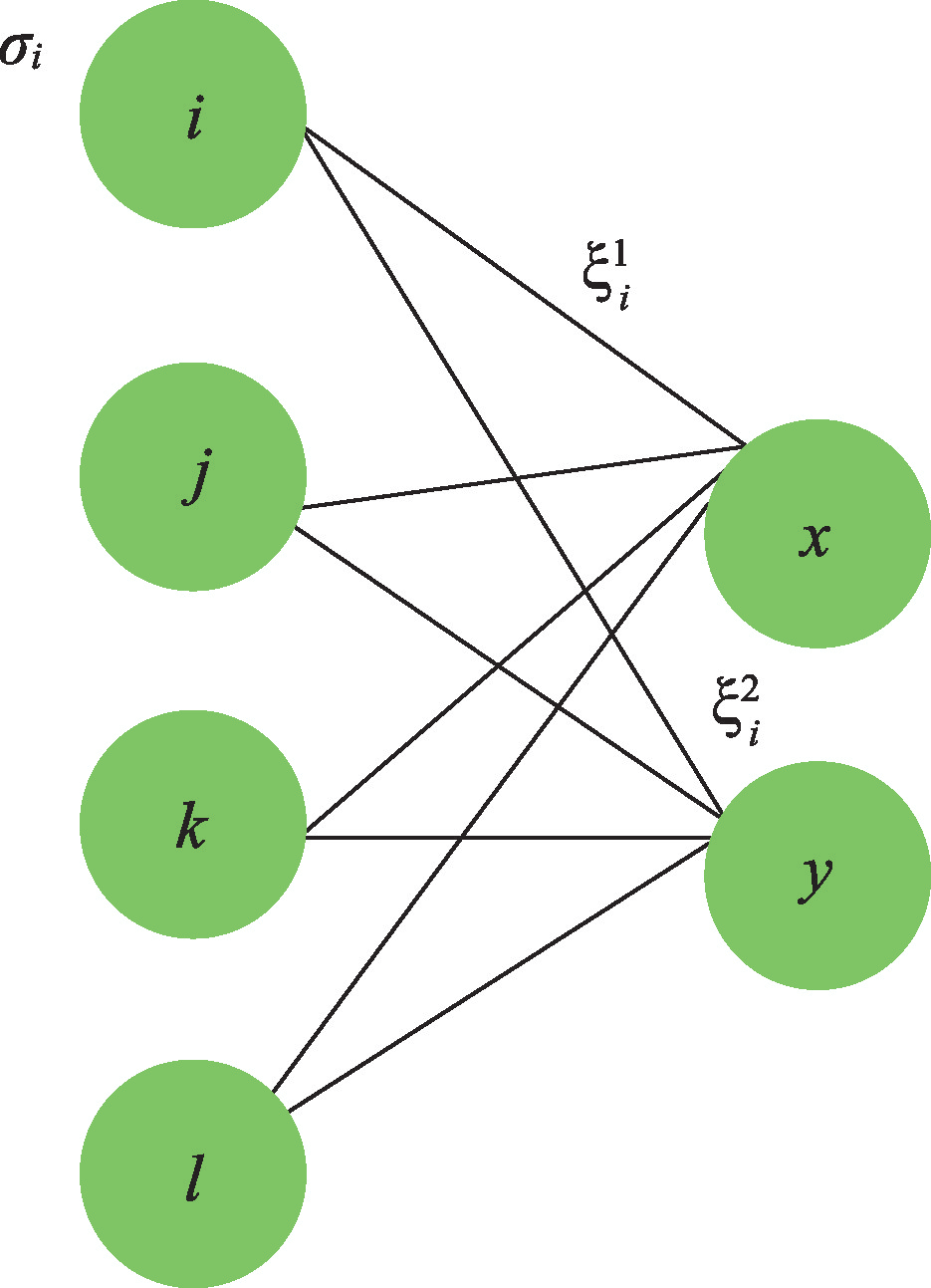
圖3 受限玻爾茲曼機的學習過程示意圖
接下來,我們容易通過貝葉斯定理寫出如下的學生網絡的概率分布:
![]()
該分布在圖3的具體表示為[10]:

其中,Z 為網絡結構的配合函數,N為每個隱層神經元的神經連接數,β為溫度倒數,P0 為先驗分布,Ω則為無監督學習的配分函數。在這里,我們做了兩個重要假設:每個數據是獨立生成的,并且先驗分布對神經元標號是獨立的。我們稍微觀察以上的系綜分布就可以發現,ξ1,2 → -ξ1,2 和12,該分布是不變的,顯示了![]() 和
和![]() 對稱性,因為我們的連接權重取為Ising 自旋值。那么,一個有趣的物理問題就產生了:學習的過程是對稱性破缺的過程嗎?
對稱性,因為我們的連接權重取為Ising 自旋值。那么,一個有趣的物理問題就產生了:學習的過程是對稱性破缺的過程嗎?
經過復雜的計算(細節參看文獻[3]),我們發現:隨著數據量的增長達到第一個閾值,與![]() 對稱性相關的第一個連續性相變發生,學生開始推斷老師連接權重相同的那部分(即ξ 1i = ξ 2i),這種類型的轉變被稱為自發對稱破缺,就像在標準伊辛模型中遇到的鐵磁相變那樣。隨著數據量進一步增加,學生開始推斷老師連接權重不同的那部分( 即ξ1i= -ξ 2i),這被稱為第一種置換(
對稱性相關的第一個連續性相變發生,學生開始推斷老師連接權重相同的那部分(即ξ 1i = ξ 2i),這種類型的轉變被稱為自發對稱破缺,就像在標準伊辛模型中遇到的鐵磁相變那樣。隨著數據量進一步增加,學生開始推斷老師連接權重不同的那部分( 即ξ1i= -ξ 2i),這被稱為第一種置換(![]() )對稱破缺,即學生開始意識到它的兩個感受野( ξ1,ξ 2 )也是不同的。不妨總結為“先求同,后存異”。隨著數據量進一步增加,學生開始能夠區分老師(或基本規律)體系結構中兩個隱藏節點的內在順序。我們將這個轉變稱為
)對稱破缺,即學生開始意識到它的兩個感受野( ξ1,ξ 2 )也是不同的。不妨總結為“先求同,后存異”。隨著數據量進一步增加,學生開始能夠區分老師(或基本規律)體系結構中兩個隱藏節點的內在順序。我們將這個轉變稱為![]() 對稱性破缺的第二個亞型。僅在此轉變之后,自由能才有兩個同等重要的谷底。但學生只推斷其中一種可能性,并取決于初始條件。這兩個谷底對應于基本規律的兩種可能順序(x, y)或(y,x),這也是原始無監督學習概率分布的內在置換對稱性。因此,通過統計物理分析,我們得出:數據可以自發驅動層級式的連續相變直至數據中的客觀規律被機器所捕獲,并且也揭示了先驗的作用:極大減少自發對稱破缺的最小數據量,并且融合了兩個亞型,即在先驗的幫助下,學生認識自我和客觀是同時發生的;然而在沒有先驗情況下,認識自我則先于客觀。
對稱性破缺的第二個亞型。僅在此轉變之后,自由能才有兩個同等重要的谷底。但學生只推斷其中一種可能性,并取決于初始條件。這兩個谷底對應于基本規律的兩種可能順序(x, y)或(y,x),這也是原始無監督學習概率分布的內在置換對稱性。因此,通過統計物理分析,我們得出:數據可以自發驅動層級式的連續相變直至數據中的客觀規律被機器所捕獲,并且也揭示了先驗的作用:極大減少自發對稱破缺的最小數據量,并且融合了兩個亞型,即在先驗的幫助下,學生認識自我和客觀是同時發生的;然而在沒有先驗情況下,認識自我則先于客觀。
從一個簡單模型出發,我們可以揭示無監督學習豐富的物理圖像,即對稱性破缺是支配學習過程的重要力量。這種概念在今年又在非平衡的生成擴散過程中被完整詮釋[11],讓人不得不感嘆物理思維的巧妙與精確,再次印證了著名物理學家戴森那句名言。
04 非平衡穩態動力學的偽勢表示法
前面兩個例子并未涉及動力學,然而動力學是理解大腦認知的關鍵過程。我們注意到,在神經網絡訓練過程中,前面提到其本質為梯度力作用下的朗之萬方程。事實上,在認知動力學層面上,幾乎所有的動力學并不存在梯度力,即下面方程
dx/dt= f (x) + ζ,
其中f 為不顯含時間,但并不能寫為某個標量勢的梯度,即不存在李雅普諾夫函數。ζ表示神經回路的背景噪聲(在這里暫且將其忽略)。在高維空間里,如上的動力學方程可以涌現出混沌行為,成為眾多理論神經科學家(實際上多數為理論物理出身)展示數學物理功力的首選研究對象。在過去三十多年來,經典工作不斷涌現,每次都加深了人們對于高維混沌動力學的理解。
圖4 給出了一個3 維的例子:只有三個神經元的系統,在它們連接矩陣屬性改變時,系統的相空間由一個全局穩定點破缺為對稱的兩個焦點。雖然原系統無法通過梯度力來研究(不存在李雅普諾夫函數),但是如果變換研究的興趣為非平衡穩態(即零速率極限,即f=0),那么我們就可以非常直觀地寫下一個動能函數E(x) = (1/2)f 2 (單位質量)來作為非平衡穩態的偽勢[12],這個偽勢將讓我們能夠定義正則系綜來研究非平衡神經動力學穩態問題;這在此前的所有研究中是無法想象的。原則上,人們應該通過復雜的動力學平均場或路徑積分來推導穩態方程,這對于更復雜的神經動力學(比如f 的形式較復雜)來說甚至是十分艱巨的一個計算任務。
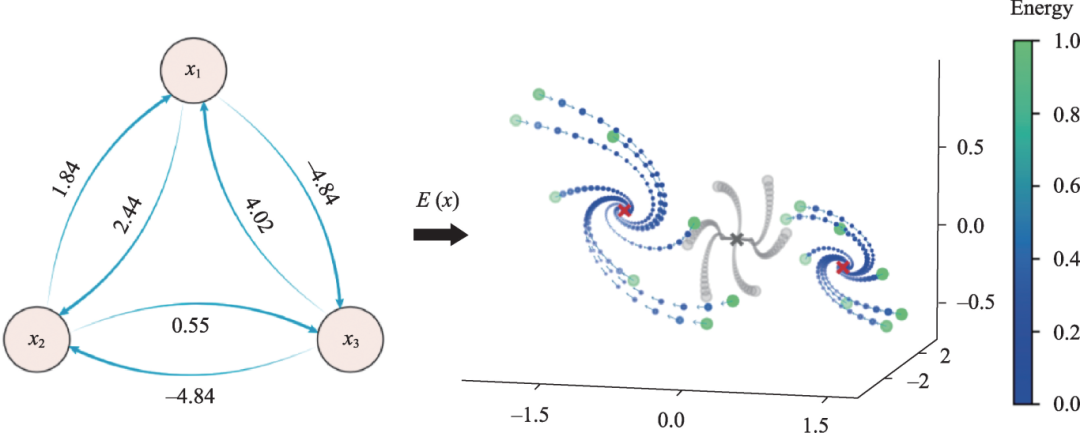
圖4 非線性動力學的偽勢法
有了這個新思路,當三個神經元系統被推廣至無窮(N→∞)神經元系統(比如大腦具有大概860 億級的神經細胞),并且假設相互作用矩陣是非厄米的隨機矩陣[矩陣元Jij ~N(0,g2 /N) ],我們可以發現當g 增加到1 時將觸發一個連續的動力學相變(從有序走向混沌),其序參量為網絡神經活動水平的漲落。注意這些序參量并不是人為設定的,而是來源于上面正則系綜計算的邏輯演繹。讓人驚訝的是,該計算還會導出另一個序參量,恰是統計力學中的響應函數,它刻畫了動力系統在面對微弱擾動時的響應能力。我們發現在相變點附近,該響應函數出現峰值,從物理上證實了混沌邊緣的優越性。無獨有偶,2022 年的一項實驗研究表明人類大腦的腦電動力學在清醒時在混沌邊緣具有最大的信息豐度[13],從而暗示了統計力學推導的響應函數峰值可能從數學上講是意識的必要條件。
這個例子告訴我們,即便是十分復雜的非梯度動力學,我們依然可以另辟蹊徑從統計力學角度提出模型,并且通過嚴謹計算獲得深刻認識。因此,年輕學生應該掌握必要的數學工具,并且勇于挑戰既有思想框架,通過提供新的見解來發展古老的學科。
05 大語言模型示例泛化的奧妙
大語言模型是2023 年初火遍全球的Chat GPT的原動力,它憑借海量數據文本和計算力通過預測下一個單詞贏得了世人的贊嘆和興趣[14]。經過預訓練的聊天工具尤其展示了一種示例泛化的能力,這在以往所有機器模型中均未出現過。簡單來說,就是給少數幾個例子(不管是數學的,還是語言的),然后基礎模型也不用再訓練,它就能夠對新問題給出準確答案了。這困惑了大家好一陣子,直到下面的事情發生。
我們說過,任何一種復雜現象都需要模型驅動的研究,才能找到潛藏的簡單規律(如果存在)。為了找到答案,我們先考慮一個線性回歸函數類,如 y = wTx 。我們首先固定一個隨機的任務向量w,然后生成多個隨機的x 計算其標簽y,就有了針對示例泛化的預訓練數據:
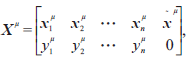
注意最后一列為讓基礎模型推斷的數據,故遮掉了真實的標簽。這個矩陣相當于給了有答案的n道數學題,然后問一道(最后一列),看機器能否準確推斷。這顯然是一個難的問題!但是,神奇的是,聰明的機器做到了,不禁讓人看到通用人工智能微弱的曙光。
其實通過簡單變換,比如假設單層線性自注意力機制(細節見文獻[15]),我們喜出望外地發現預訓練的機器參數服從如下的哈密頓量:
![]()
最后一項為機器參數的高斯先驗。這顯然是一個兩體相互作用的實自旋模型,它的基態就是基礎模型示例泛化能力的根源。我們可以通過高斯分布假設來求解這個模型的基態,最后發現哪怕在有限尺寸的網絡,依然可以得到如下最優解:
![]()
其中![]() 為神經網絡給出的答案,上述物理模型的基態意味著
為神經網絡給出的答案,上述物理模型的基態意味著![]() 和W21=0,D 是數據的維度。分塊矩陣W與自旋耦合J 一一對應。因此我們就明白了,只要找到該基態,示例泛化即可達成,并無需再微調參數!這個模型還揭示了任務向量的多樣性對預訓練效果起到至關重要的作用。因此,也就不難理解大語言模型需要海量多模態的文本庫了。我們可以大膽地想象,只要窮盡承載人類文明的所有知識,也許有一天我們真能制造出無所不能的智慧機器,至少在人類已掌握技能的疆域內是沒有問題的。
和W21=0,D 是數據的維度。分塊矩陣W與自旋耦合J 一一對應。因此我們就明白了,只要找到該基態,示例泛化即可達成,并無需再微調參數!這個模型還揭示了任務向量的多樣性對預訓練效果起到至關重要的作用。因此,也就不難理解大語言模型需要海量多模態的文本庫了。我們可以大膽地想象,只要窮盡承載人類文明的所有知識,也許有一天我們真能制造出無所不能的智慧機器,至少在人類已掌握技能的疆域內是沒有問題的。
06 總結和展望
本文從物理學的概念出發介紹了神經網絡的DNA,數據相當于一種初始化,可以驅動網絡連接權重的連續更新以獲得一個聰明的自適應的物理模型,而這個更新過程是端對端地優化一個目標函數,優化的過程即執行在高維空間的朗之萬動力學。神經網絡的奧秘正是在于高維的權重空間,它本質上服從正則系綜分布。半嚴格的物理分析給出了權重空間的分布和數據驅動的權重的對稱性破缺。從物理直觀出發,人們可以獲取非平衡神經動力學的穩態全貌以及隱藏的動力學相變;甚至,人們可以將大語言模型的示例泛化歸結為兩體自旋模型,依此可以洞察智能的本質。數學的具象化為物理,而物理的盡頭則為數學,數學與物理相輔相成,成為理解神經網絡乃至智能本質不可或缺的手段。本文借助少數幾個例子,希望啟發青年學生欣賞數學的魅力,習得物理的洞察力,為揭開大腦智能神秘的面紗貢獻自己的智慧。
參考文獻:
參考文獻(一)
① 神經網絡的源頭可追溯至麥可洛和皮茨在1943年發表的關于邏輯演算的研究。
② 戴森應邀為美國數學會的愛因斯坦講座所準備,題目為鳥與青蛙。
③ 大模型的壓縮并不意味著“理解”。
④ 對受限玻爾茲曼機訓練算法的研究是2024年諾貝爾物理學獎得主辛頓的重要貢獻之一。
參考文獻(二)
[1]Ising,E.Beitrag zur Theorie des Ferromagnetismus. Z. Physik, 1925, 31: 253-258 。
[2] 黃海平, 統計物理、無序系統與神經網絡, 科學,2022,74:40-44
[3] 黃海平,神經網絡的統計力學(英文版),高等教育出版社,2021.
[4] Brice Huang, Capacity threshold for the Ising perceptron, arXiv:2404.18902.
[5] H. Huang, K. M. Wong and Y. Kabashima, Entropy landscape of solutions in the binary perceptron problem, Journal of Physics A: Mathematical and Theoretical, 2013, 46(37):375002; H.Huang andY. Kabashima, Origin of the computational hardness for learning with binary synapses, Physical Review E, 2014, 90(5):052813.
[6] W. Perkins and C. Xu, Frozen 1-rsb structure of the symmetric ising perceptron, Random Structures & Algorithms, 2024, 64(4):856.
[7] E. Abbe, S. Li and A. Sly, Proof of the contiguity conjecture and lognormal limit for the symmetric perceptron, In 2021 IEEE 62nd Annual Symposium on Foundations of Computer Science (FOCS), pp. 327-338.
[8] C. Baldassi, A. Ingrosso, C. Lucibello, L. Saglietti and R. Zecchina, Subdominant dense clusters allow for simple learning and high computational performance in neural networks with discrete synapses, Physical review letters, 2015, 115(12):128101.
[9] E. Abbe, S. Li and A. Sly, Binary perceptron: efficient algorithms can find solutions in a rare well- connected cluster, In 2022 Proceedings of the 54th Annual ACM SIGACT Symposium on Theory of Computing, pp. 860-873.
[10] Tianqi Hou and Haiping Huang. Statistical physics of unsupervised learning with prior knowledge in neural networks. Phys. Rev. Lett., 2020, 124:248302
[11] Gabriel Raya and Lca Ambrogioni. Spontaneous symmetry breaking in generative diffusion models. In A. Oh, T. Neumann, A. Globerson, K. Saenko, M. Hardt, and S. Levine, editors, Advances in Neural Information Processing Systems, volume 36, pages 66377-66389. Curran Associates, Inc., 2023; Z. Y and H. Huang, Nonequilbrium physics of generative diffusion models, arXiv: 2405.11932.
[12] Junbin Qiu and Haiping Huang. An optimization-based equilibrium measure describes non- equilibrium steady state dynamics: application to edge of chaos. arXiv:2401.10009.
[13] Daniel Toker, Ioannis Pappas, Janna D Lendner, Joel Frohlich, Diego M Mateos, Suresh Muthukumaraswamy, Robin Carhart-Harris, Michelle Paff, Paul M Vespa, Martin M Monti, et al. Consciousness is supported by near- critical slow cortical electrodynamics. Proceedings of the National Academy of Sciences, 2022, 119(7):e2024455119.
[14] Sebastien Bubeck, Varun Chandrasekaran, Ronen Eldan, John A. Gehrke, Eric Horvitz, Ece Kamar, Peter Lee, Yin Tat Lee, YuanFang Li, Scott M. Lundberg, Harsha Nori, Hamid Palangi, Marco Tulio Ribeiro, and Yi Zhang. Sparks ofartificial general intelligence: Early experiments with gpt-4. arXiv:2303.12712.
[15] Yuhao Li, Ruoran Bai, and Haiping Huang, Spin glass model of in-context learning, arXiv: 2408.02288.
-
神經網絡
+關注
關注
42文章
4777瀏覽量
100953 -
人工智能
+關注
關注
1792文章
47513瀏覽量
239227
原文標題:神經網絡理論研究的物理學思想
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 神經網絡理論研究的物理學思想介紹
神經網絡理論研究的物理學思想介紹
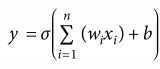










評論