電容的本質是一個容器。就好像一個蓄水池，既能存水，又能從中取水；又好像一個儲錢罐子，既能存錢，又能從中取錢。

1 ‘藏’

存儲電荷的容器，稱為電容。

所有傳遞給電阻的能量都以熱量的形式被消耗掉，但是電容不會。

所以，電容是一個儲能元件。

這種特性，我將其描述為一個字：“藏”。

電容的一切應用，都源自于“儲藏”。

2 基礎公式與推論

任意兩塊平行金屬板就能構成一個簡易電容器。給極板兩側通上電的瞬間便完成了電荷的“儲藏”過程，使得上極板充滿正電荷，下極板全是負電荷。

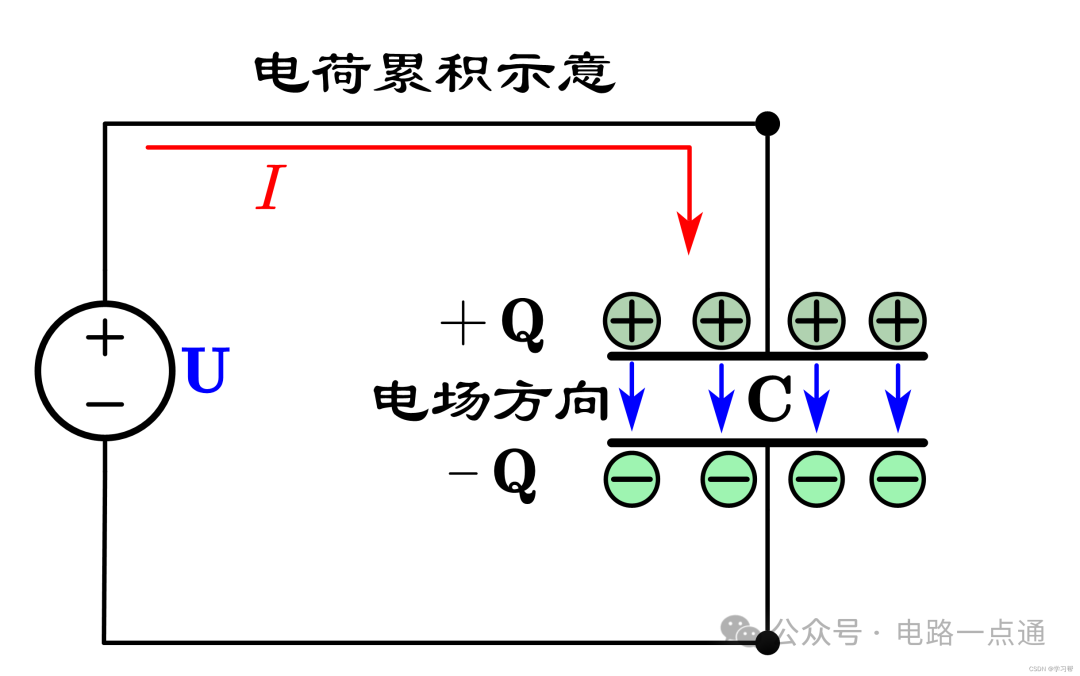
儲藏的電荷來自于電源，極板電容兩端的電壓越大，儲藏的電荷越多。

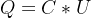
“儲藏”電荷需要一定的時間，該過程的電荷移動形成了電流。

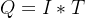
在極短的時間內，電荷移動產生了多少電流？結合微積分，便有了電容的核心公式：

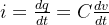
核心公式的直觀理解與推論：

電容越大，儲藏的電荷就越多，因而可以提供更多的電流

推論1：電容可以用做負載的電流小金庫，以備不時之需 推論2：電容可視為一個小型電荷泵，電荷取用自由

電壓變化地越快，得到的電流就越大

推論3：電路上下電瞬間，電壓突變，導致電容兩端的電流突變 推論4：由電路上下電造成的電流尖峰，稱之為浪涌電流

電流的大小取決于電容兩端電壓的變化率，和電容本身大小無關

解釋：電容一旦制作完成，其容值便基本固定，因此dv/dt起決定作用

進一步推導出電容“儲藏”的能量：

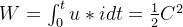
基于直流電源基礎上的公式推導，如上文所述。

如果面對的是交流電，此時的公式是否會產生某些變化？

將正弦交流電壓，帶入核心公式，可得到電流的交流形式：

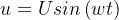
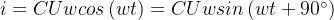
運用歐姆定理，便得到電容的容抗表達式：

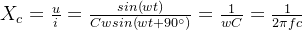
從容抗表達式，能看出：

通高頻，通交流

解釋：當處于高頻交流電路中時，容抗X十分小，不具有“抵抗”作用，很容易通過

阻低頻，阻直流

解釋1：低頻電路，容抗X特別大，“抵抗”力十足，將低頻信號隔絕在外 解釋2：直流，是頻率為0的交流信號

3 高頻模型

為簡化計算，運用理想平行板電容模型參與簡單計算。

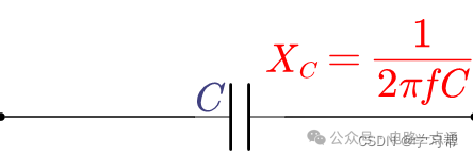
受到實際生產制造工藝的局限，真實電容帶有許多寄生參數。這些寄生參數在高頻中會帶來較大的影響，難以忽略。

如填充在極板間的介質很難做到完全絕緣；如存在于引線上的電阻/電感等......

應用中，會綜合考慮這些寄生參數，用等效串聯電阻ESR模擬參數中的阻性；用等效串聯電感ESL模擬參數中的感性。這兩個參數會帶來一定的損耗，如漏電流等。

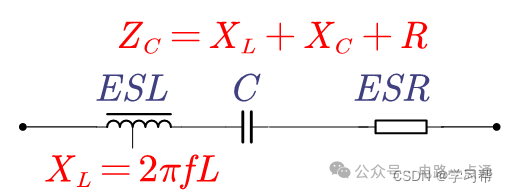
從高頻阻抗公式，能看出：

電容介質損耗

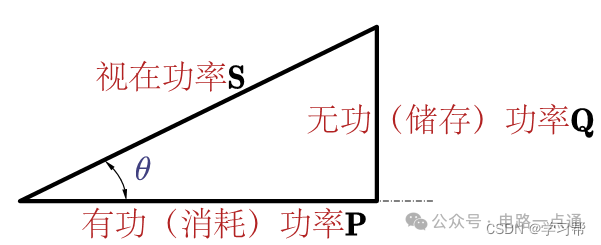
引入3種功率，儲存功率（無功功率Q）,消耗功率（有功功率P），視在功率S，三種功率組成功率三角形，如上圖所示。引出電容介質損耗：

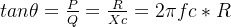
諧振頻率點

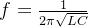
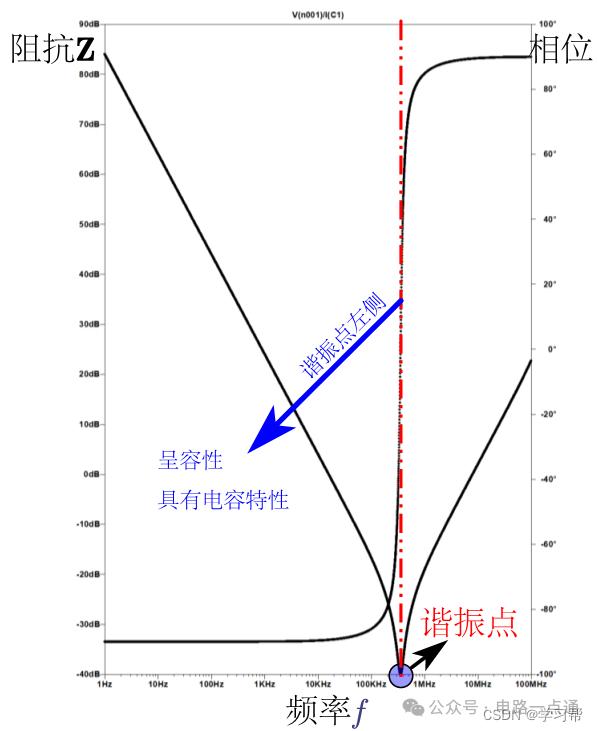
從公式可以看到：

1諧振點處，電容呈現純阻性 2影響諧振頻率的參數，主要是ESL和容值 3顯然容值越大，諧振頻率越小（和容值相比，ESL的數值幾乎可以忽略）

不同容值的阻抗頻率曲線如圖所示：

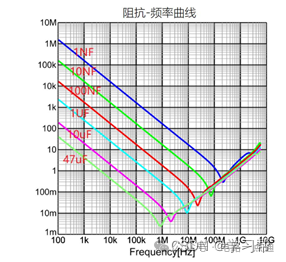
4 兩組六大參數

仿照電阻參數，本文將電容參數劃分成2組，細分為6小個。分別是：

物有形---封裝、容值

物有實---材料、溫漂、精度、耐壓

容值刻度、以及耐壓等參數通常會標注在插針式電容表面；而對于貼片式電容，由于表面積不足，因而只能看到簡單的幾何外形。

參數1：封裝

常見貼片式和插針式兩種。貼片式的器件需要使用回流焊，插針式使用波峰焊進行焊接。對于貼片式的封裝，又根據大小分為0805、0603等。

回流焊：使用高溫熱風使涂在焊盤表面的錫膏融化，進而形成焊點 波峰焊：一種手焊的機械自動化形式，用熔融態的錫去觸碰針腳

參數2：容值

容值的單位記憶小口訣，皮納微法。每個字之間相差1000倍。

參數3：溫漂

同電阻一樣，這是一個材料精度。容值隨溫度的變化率，單位ppm/℃。

參數4：精度

純正反映制造水平的參數，水平高，精度高。

參數5：耐壓

標稱最大工作電壓，和電容的尺寸、材料均有關。

參數6：材料

以貼片式陶瓷電容為例，俗稱MLCC。按材料特性可將其分為兩類，第一類電容和第二類電容。

第一類電容：代表C0G，適用于高頻電路的濾波、耦合等，容值穩定可靠。

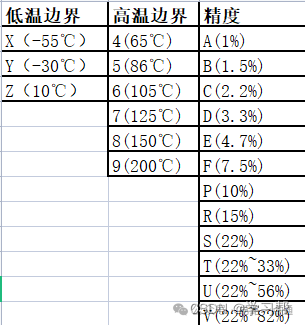
第二類電容：代表X7R，穩定性較差，DC偏壓特性差【電容量隨直流電壓的瞪大而減小】，此類電容命名以溫度-精度著稱，常見的幾大類如下表所示：

5 RC積分電路

RC電路是阻容系統中的最簡形式。這個電路有兩個變種，一種電容接地，一種電阻接地。山河主講電容接地的變種，即RC積分電路。

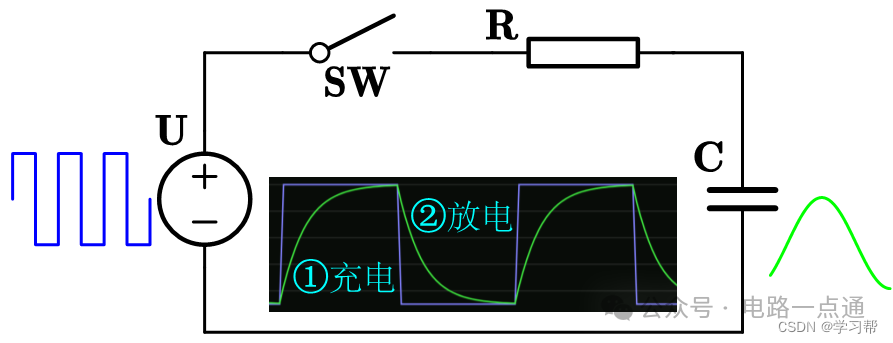
前面咱說，電容是一個水池。

那么無論是從中取水，或者將水池裝滿，都需要一定的時間。

時間常數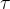具有如下定義，單位：秒，反映充放電的快慢

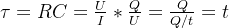
階段1：充電

充電過程電壓表達式，其圖像恰如上圖中綠色部分。

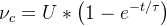
從電壓表達式，能了解到如下信息

1.充電開始的瞬間，電容兩端電壓為0，等價為導線，必然產生電流 2.充滿電的時間大概是5τ，此時大概充到99.3%的程度 3.充電完成時，電容兩端的電壓約等于電源，視為電容開路 4.電壓的主要變化過程，體現在第一個τ內 5.電容兩端的電壓是緩慢增加的

上述就是“電容兩端的電壓不能突變”的原因。

其實從公式Q=CU同樣能推導出“電容兩端的電壓不能突變”，因為電荷的累積不可能一蹴而就。

充電過程的電流表達式，其圖像如下圖橙色曲線所示

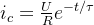
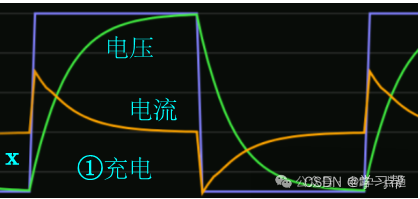
從電流表達式，能了解到：

1.充電開始的瞬間，電容兩端存在電流，即電壓為0，電流不為0 2.初始電流尖峰，隨充電時間增加而減小

提個問題，上圖中標記X處，為什么沒有重合？即電流電壓曲線起始點為何沒有重合？

因為，起始點處電容形同一根導線，因此導線中會有電路的電流。

一旦充電開始，電容上會產生一個電流尖峰，稱之為“浪涌電流”。

除了“浪涌電流”外，還能看出一個概念，DC偏壓特性。顯然充電過程中，電壓不斷增加，電流不斷減小。

電流的減小，說明電容的容抗在增加。

電壓在增加，根據C=Q/U知，容值在動態減小，因此容抗在增加。

即，DC偏壓特性是電容特有屬性，但是X7R材質的電容相較于C0G的要差許多，也因此會有更陡峭的浪涌電流

階段2：放電

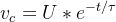
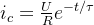
放電過程就是充電的逆過程，電壓仍然沒有突變，浪涌電流仍然存在

怎樣統一充放電過程？

其實很簡單，之前我們一直假想的是從“0”開始充電，而這在實際應用中，幾乎是不可能的。因此，就有了如下統一公式：

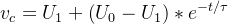
U0：初始電壓，如果為0，就成了理想充電過程 U1：終點電壓，如果為0，就成了理想放電過程

6 時間常數

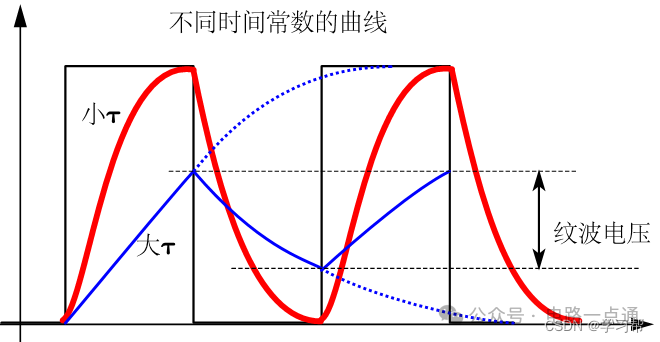
再來看看不同時間常數，對充放電電壓/電流的影響。

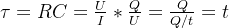
時間常數越小，充滿電的時間越短，電壓/電流的上升沿越陡峭，這將會帶來兩個影響，其一，引入較大的浪涌電流；其二，造成比較惡劣的EMC結果。

時間常數過大，曲線上升緩慢，甚至在電壓脈沖周期結束時，充電尚未完成就立馬轉入放電周期。這種現象會給后級電路帶來紋波電壓。

另一方面，時間常數過大或者過小，都會導致后級ADC采樣失準。即原本需要對1.2V采樣，但因為時間常數的緣由，采集到的真實電壓大于/小于1.2V，進而造成ADC采樣轉化上面的數值偏差。

前文都是在假設電源頻率不變的基礎下，增大/減小時間常數，進而導致充放電曲線的緩/抖。

換一個角度，時間常數固定不變，改變電源的頻率，會發生什么？

以實際應用中比較常見的場景，PWM信號的濾波電容，它的充放電波形是什么樣的？

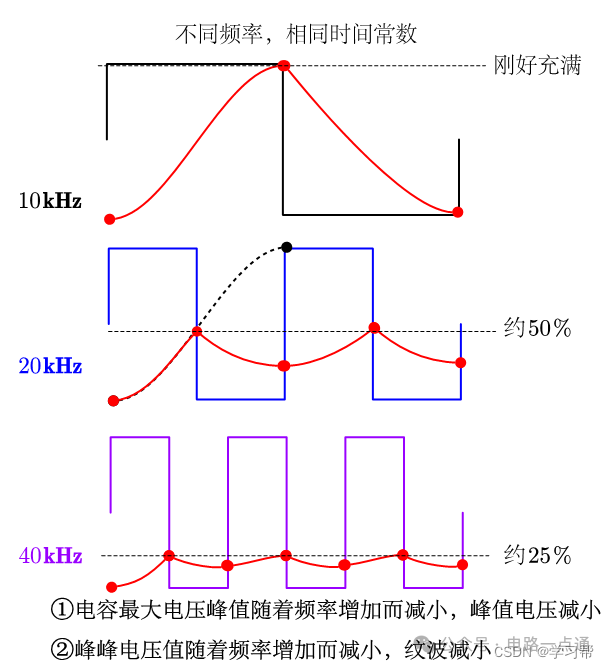
即如下兩個操作對充放電曲線而言是幾乎等價的：

CASE1:PWM頻率不變，增大時間常數 CASE2:時間常數不變，增大PWM頻率

能看到一個顯著趨勢：頻率越快，電容輸出電壓的幅值越小。

但是，一旦頻率增加到截止頻率時，輸出電壓將不會再有變化。

這便是為什么RC積分電路，又被稱作“低通濾波器”。低通，藏掉高頻。

7 容值計算

在大多數直流系統中，電源端進來的第二個單元就是濾波，那么這個電容的容值該如何設計呢？利用電荷量守恒建立方程，即：

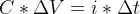
假設12V，30A，±1%紋波精度，紋波頻率400kHz的直流系統，則其紋波電壓為：

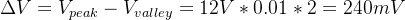
紋波頻率決定了電容的有效充放電時間，因此在占空比50%的電源系統中，電容的充電時間為:

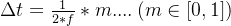
從而計算出電容的容值為：

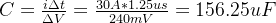
進一步考慮電容不同的選值系列，并考慮一定的冗余，確定最終的電容值。

電容容值選擇偏大/偏小帶來哪些影響？

選大了，容器大了，能藏的東西更多了，呈現出來就是紋波更小，但是電容的價格也會隨之上漲。 選小了，容器小了，藏不住東西，一藏就滿，一掏就空，呈現出來就是曲線的斜率大，容抗也大，由于ESR的存在，導致紋波電壓大，更是會產生熱量，導致電容壽命下降。

選不到自己想要的容值怎么辦？

跟電阻一樣，將電容串并聯以獲取自己需要的容值。

8電容的應用

回到開頭，電容善藏。

電容最重要的應用，就是濾波、儲能。前者藏無用，后者藏有用。