C28x+FPU架構的C2000微處理器在原有的C28x定點CPU的基礎上加入了一些寄存器和指令，來支持IEEE 單精度浮點數(shù)的運算。對于在定點微處理器上編寫的程序，浮點C2000也完全兼容，不需要對程序做出改動。浮點處理器相對于定點處理器有如下好處：

編程更簡單

性能更優(yōu)，比如除法，開方，F(xiàn)FT和IIR濾波等算法運算效率更高。

程序魯棒性更強。

一、IEEE754格式的浮點數(shù)

C28x+FPU的單精度浮點數(shù)遵循IEEE754格式。它包括：

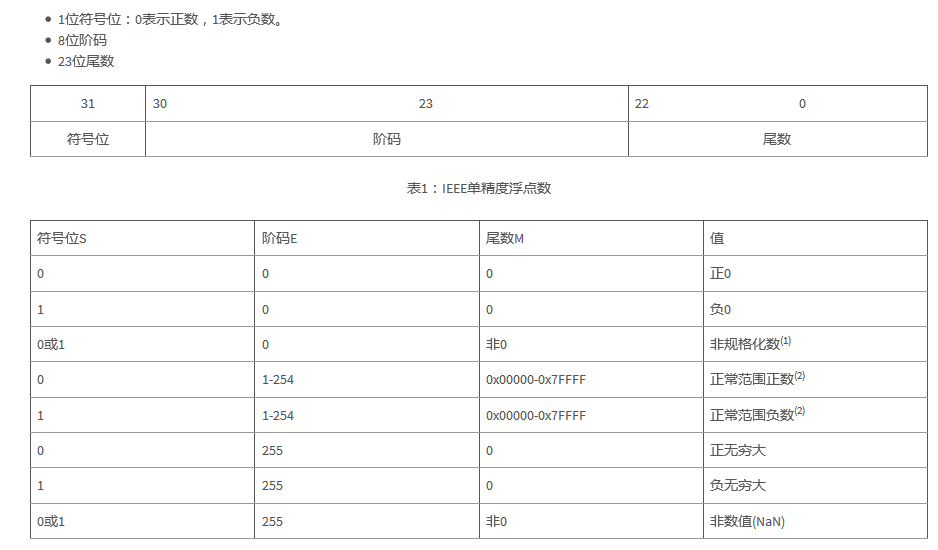
尾數(shù)

表1：IEEE單精度浮點數(shù)

(1)非規(guī)格化數(shù)值非常小，計算公式為(-1)sx2(E-126)x0.M

(2)正常范圍數(shù)值計算公式為(-1)sx2(E-127)x1.M

正常范圍數(shù)值落在± ~1.7 x 10 -38 to ± ~3.4 x 10 +38范圍內(nèi)。從表1可以看出，IEEE754標準包括：

標準數(shù)據(jù)格式和特殊值，比如非數(shù)值(NaN)和無窮大

標準舍入模式和浮點運算

多平臺支持，包括德州儀器C67x系列芯片。

C2000對該標準作了一些簡化：

狀態(tài)標志位和比較運算不區(qū)分正0和負0

非規(guī)格化數(shù)值被認為是0

對非數(shù)值(NaN)處理方式和無窮大一樣。

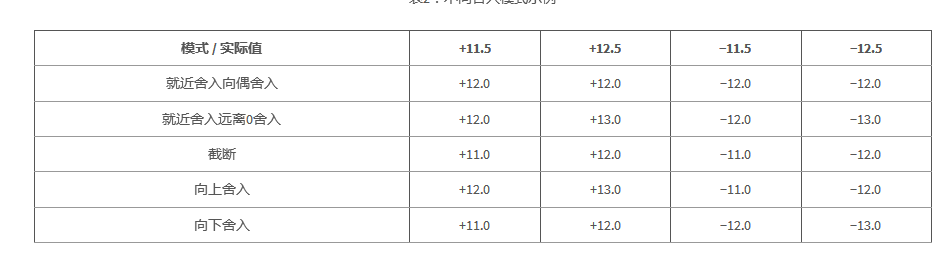
IEEE754標準有5種舍入模式，C28x+FPU只支持其中兩種：

--截斷：小數(shù)位不管大小全部舍去

--就近舍入向偶舍入：這種模式下如果小數(shù)位小于5就舍去，大于5就進位，如果小數(shù)位為5，則舍入到最近的偶數(shù)。

表2展示了不同的舍入模式對數(shù)據(jù)的影響。C28x+FPU編譯器默認將微處理器配置為就近舍入向偶舍入模式[1]。

表2：不同舍入模式示例

??

二、浮點C2000芯片運算技巧和注意點

浮點數(shù)的精度由尾數(shù)位決定，絕大多數(shù)的數(shù)在用浮點數(shù)表示時都會有誤差，這些誤差很小，多數(shù)情況下可以忽略，但是在經(jīng)過多次計算后這個誤差可能會大到無法接受。

下面用實例來進行說明，下面一段代碼定義float類型變量，分別在TI最新的Delfino芯片F(xiàn)28379D的CPU1和CLA1上，將11.7加20001次。

float CLATMPDATA=0;

int index=20001;

while(index--)

{

CLATMPDATA=CLATMPDATA+11.7;

}

得到如下結果：

其中CLATMPDATA1是在CLA中將11.7加20001次得到的結果，CLATMPDATA2是在CPU中將11.7加20001次得到的結果。可以看出兩者所得到的結果不同，并且都和正確結果234011.7有較大差距。

為何CPU和CLA計算結果不同？

CPU和CLA運算結果的不同是由于其對浮點數(shù)的舍入模式的不同造成的，前文已經(jīng)說過，C28x+FPU 編譯器默認將CPU配置為就近舍入向偶舍入模式。而CLA不同，CLA默認為截斷舍入模式[2]。在CLA的代碼中，我們可以通過增加下述代碼：

__asm(" MSETFLG RNDF32=1");//1為就近舍入向偶舍入，0為截斷舍入

將CLA的舍入模式更改為就近舍入向偶舍入模式，然后再運行代碼，可以得到和CPU同樣的結果。

2. 為何CPU和CLA計算結果都有較大誤差？如何解決？

11.7在用IEEE754格式的浮點數(shù)表示時為0x413b3333，其對應的實際值為11.69999980926513671875，可以看出誤差很小，但是經(jīng)過多次累加多次舍入后得到的結果誤差較大，對此，我們可以將CLATMPDATA定義為long double型變量（64位），再次運行相同的代碼，可以得到如下結果，可以看到誤差很小可以忽略。

需要指出的是，現(xiàn)有的C28x CPU只支持單精度（32位）的硬件浮點運算，對于64位雙精度浮點數(shù)的運算都是通過軟件實現(xiàn)的，所以其運算速率會慢很多。另外CLA不支持64位數(shù)。

在這個實例中，我們可以分別觀察float類型變量和long double類型變量的匯編代碼如下：

C code: CLATMPDATA2=CLATMPDATA2+11.7;

如果CLATMPDATA2是float型變量，則相應的匯編代碼為：

00c08d: E80209D8 MOVIZ R0, #0x413b 1cycle

00c08f: E2AF0112 MOV32 R1H, @0x12, UNCF 1cycle

00c091: E8099998 MOVXI R0H, #0x3333 1cycle

00c093: E7100040 ADDF32 R0H, R0H, R1H 2cycle

00c095: 7700 NOP 1cycle

00c096: E2030012 MOV32 @0x12, R0H 1cycle

如果CLATMPDATA2是long double型變量，則相應的匯編代碼為：

00c08b: 7680005A MOVL XAR6, #0x00005a 1cycle

00c08d: 8F00005A MOVL XAR4, #0x00005a 1cycle

00c08f: 8F40C26A MOVL XAR5, #0x00c26a 1cycle

00c091: FF69 SPM #0 1cycle

00c092: 7640C0C9 LCR FD$$ADD 4cycle（跳轉耗時）

+25cycle（FD$$ADD函數(shù)內(nèi)部需要25cycle）

可以看出CPU對float類型數(shù)執(zhí)行一次加法耗時7個cycle，對long double類型數(shù)執(zhí)行一次加法耗時33個cycle。

三、結論

1. C2000的CPU和CLA默認的舍入模式不同，在計算浮點數(shù)時可能會得到不同的結果，但是我們可以通過代碼改變其舍入模式得到相同的結果。

2. 單精度浮點數(shù)經(jīng)過多次計算后可能會有較大誤差，可以通過將變量定義為64位long double型解決精度問題。

3. C28x CPU只支持單精度（32位）的硬件浮點運算，對于64位雙精度浮點數(shù)的運算都是通過軟件實現(xiàn)的，所以其運算速率會慢很多。在下一代的C2000產(chǎn)品中我們會實現(xiàn)對64位雙精度浮點數(shù)運算的硬件支持。