0、前言

在一個閉環控制系統中，可分為輸入參考值、閉環控制器、執行機構、輸出參數，反饋系數，這幾個部分。

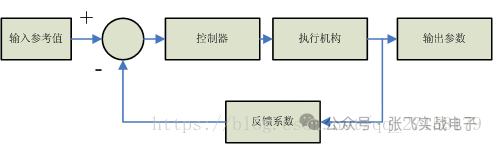
設計一款控制器，可以讓系統的輸出參數跟蹤輸入參考值，達到了控制的目的。在直流控制系統中，常用的控制器就是比例微分積分(Proportion Integration Differentiation,PID)控制器了。然而，在交流系統中，PID控制器由于對高頻信號的跟蹤性能較差，并不能滿足設計要求。而PR控制器，對特定頻率信號的跟蹤效果是良好的。

?

本文首先對PR控制器和PI控制器進行對比。然后討論了比例諧振（Proportion, Resonant, PR）控制器的數字化實現。筆者目前在一款DCDC電路中使用過PI控制器，同時PI控制器的資料比較好找。然而PR控制器只在軟件仿真中使用過，并沒有在實際項目中使用。

希望我和讀者們，都能從本文中獲益，謝謝。

1、PR控制器和PI控制器對比

1.1 傳遞函數表達式對比

比例積分控制器的傳遞函數如下：

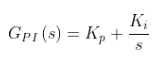
比例諧振控制器的傳遞函數如下：

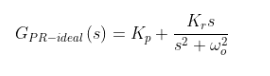
本文稱這個PR控制器為理想的PR控制器。

以上的這個控制器，在下文的波特圖上可見，只對單一的頻率起作用。但實際上，例如逆變器，參考波形可能在頻率上有正負1Hz的變化，或者由于測量采樣的不確定性，因此在運用中，會用以下的變形，替代上面的Gpr-ideal。

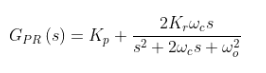
本文稱這個PR控制器為實際的PR控制器。

1.2 波特圖對比

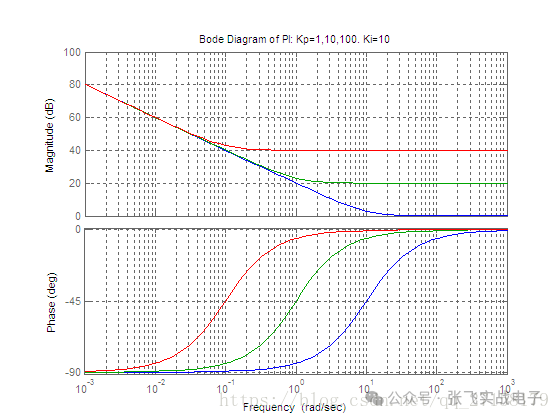
下圖是當Kp分別取為1、10、100，Ki=10時PI控制器的波特圖（藍色是Kp=1，綠色是Kp=10，紅色是Kp=100）。

附上實現代碼：

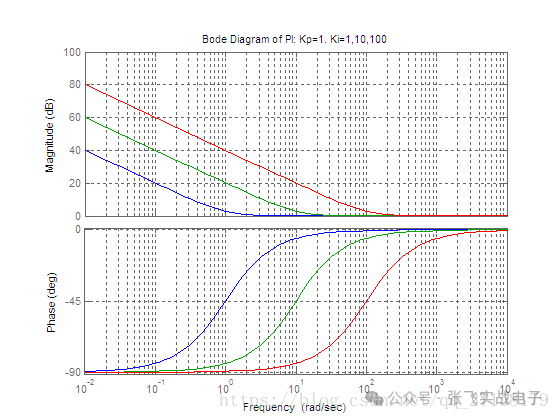
下圖是當Kp=1，Ki分別取為1、10、100時PI控制器的波特圖（藍色是Ki=1，綠色是Ki=10，紅色是Ki=100）。

附上實現代碼：

可以看到，PI控制器對高頻信號的增益會較低，而對低頻信號會有較大的放大作用。假如使用PI控制器對50Hz及以上（角頻率314rad/sec）的正弦波進行跟蹤，系統的跟蹤特性會較差。而且會把低頻噪聲放大。

下圖是當Kp分別取為1、10、100，Kr=1時理想的PR控制器的波特圖（藍色是Kp=1，綠色是Kp=10，紅色是Kp=100）。

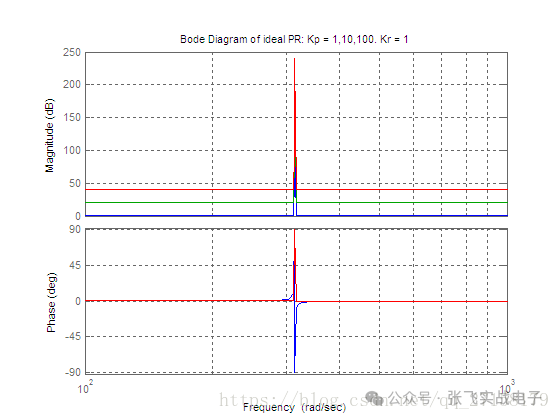
附實現代碼

下圖是當Kp=1，Kr分別取為1、10、100時理想的PR控制器的波特圖（藍色是Kr=1，綠色是Kr=10，紅色是Kr=100）。

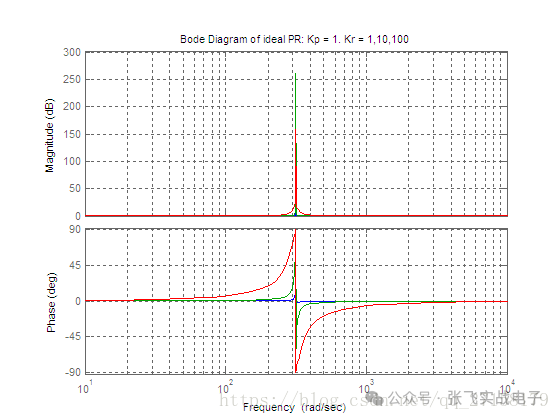
附實現代碼

上面理想PR的波特圖，可以看到就算調整PR的參數，波形也沒什么大的變化。在實際使用中，可能進行實時調參的。圖像變化這么小，跟蹤效果也不會好。

接下來看看實際使用的PR控制器的波特圖。

下圖是當Kp分別取為1、10、100，Kr=1時實際的PR控制器的波特圖（藍色是Kp=1，綠色是Kp=10，紅色是Kp=100）。

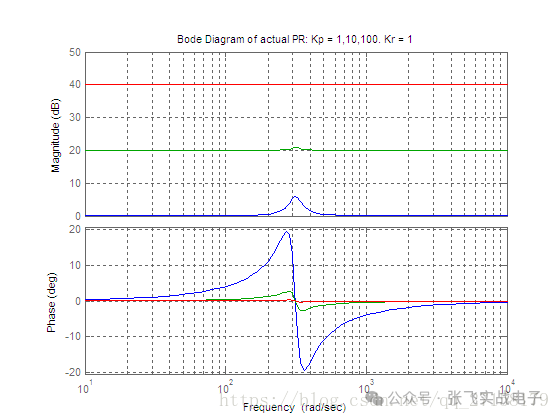
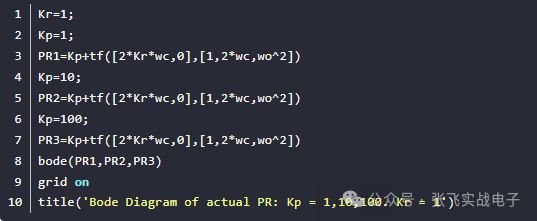
附實現代碼

下圖是當Kp=1，Kr分別取為1、10、100時實際的PR控制器的波特圖（藍色是Kr=1，綠色是Kr=10，紅色是Kr=100）。

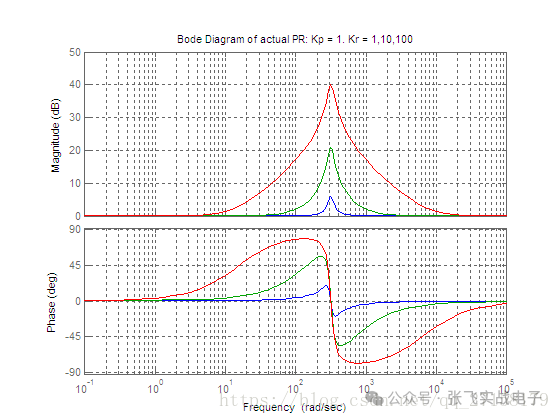
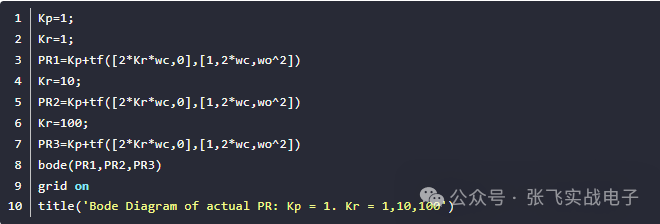
附實現代碼

PI和PR的Kp作用類似，都是增大開環增益，增加控制精度。

Ki和Kr作用類似：降低系統穩態誤差。

2、離散化預備知識

目的是對PR控制器的傳遞函數進行離散化。使其可以在數字控制器上編程實現。在這過程之前，要復習相關知識。同時便于檢查離散化過程有無錯誤。

2.1 離散化表達式

傳遞函數離散化后，函數中消掉了拉普拉斯算子“s”，同時出現了“z”。有一個公式需要認識。

以上公式，轉化為單片機或DSP可以執行的命令為：

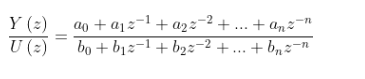
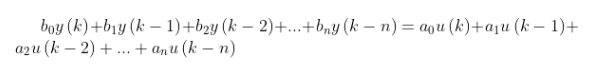
2.2 離散化方法

離散化方法一覽表[來自參考文獻1]

看起來比較簡單的方法是Forward Euler、Backward Euler、Trapezoid(Tustin)這三種了。直接把公式代入，用z消掉s就好了。

2.3 離散化練習題

用Trapezoid(Tustin)方法離散化PID控制器。

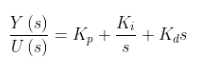
把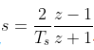代入上式，得到

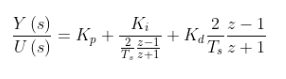
化簡過程略，得到：

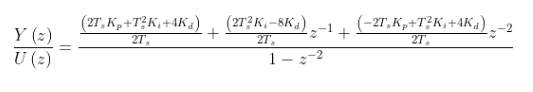
代入Kp=1；Ki=2；Kd=3；Ts=1/1000；可得到

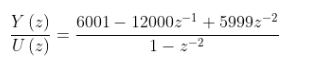
在Matlab中驗證結果：

可得到：

Transfer function:

6001 z^2-1.2e004 z+5999

---------------------------

z^2-1

Sampling time: 0.001

和計算結果一致。

同時Matlab的c2d()函數總共支持五種離散方法。

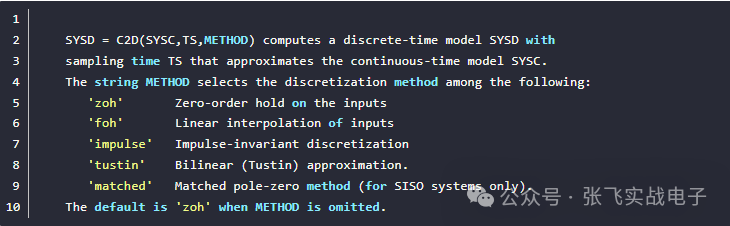
3. 使用Matlab離散PR控制器

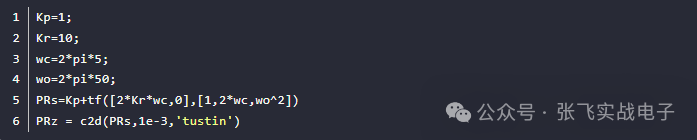
命令行輸出：

Transfer function:

1.297z^2-1.847z+0.643

---------------------------

z^2-1.847 z+0.9405

Sampling time: 0.001

可得到，離散化后，數字實現的C語言為：

y_k-1.847*y_k1+0.9405*y_k2=1.297*u_k-1.847*u_k1 +0.643*u_k2;

即

y_k=1.297*u_k-1.847*u_k1+0.643*u_k2+1.847*y_k1-0.9405*y_k2 ;

4、逆變器仿真模型中使用PR閉環控制器

Matlab/Simulink搭建了模型：

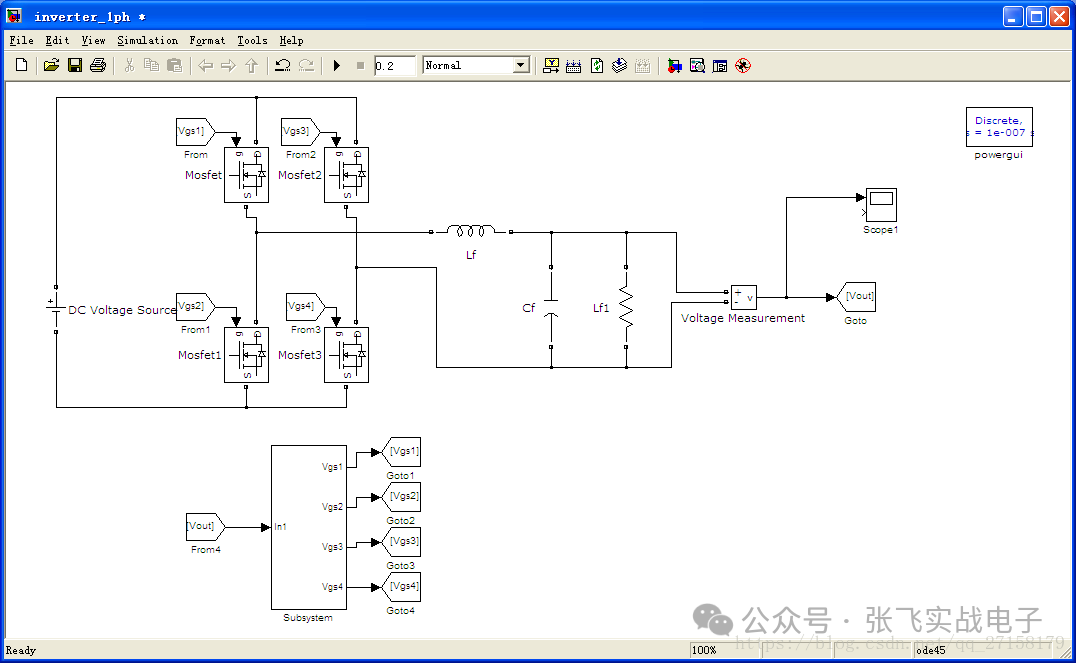
電氣主回路中參數：濾波電感Lf=47uH，濾波電容Cf=1uF，負載Lf1=30歐姆。

控制回路：

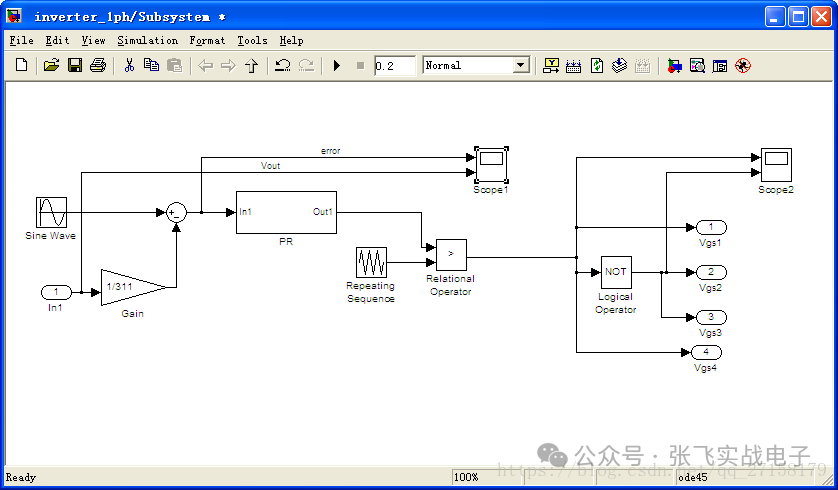
PR控制器實現框圖：

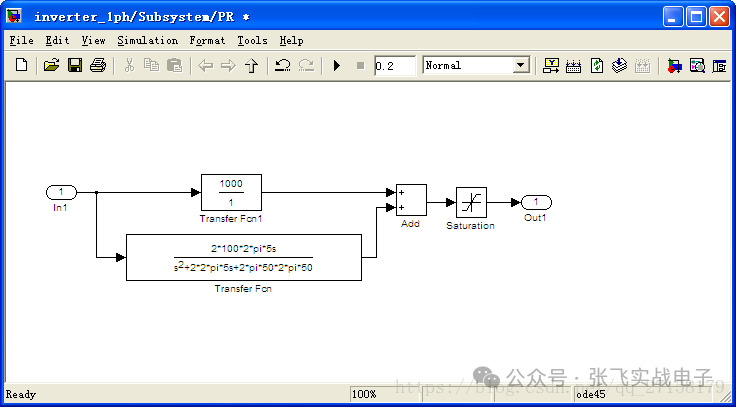
經過參數優化后，Kp=1000，Kr=100；wc=2*pi*5；wo=2*pi*50；

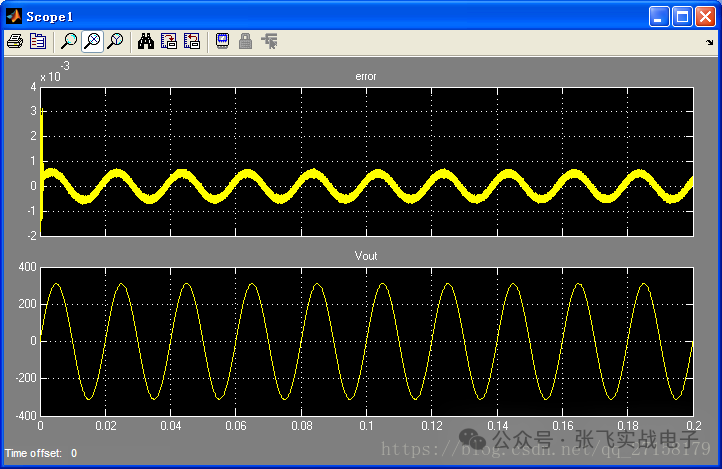
上圖中，error = Vref - Vout/311。Vref為頻率50Hz、幅值為1的正弦波。Vout是逆變器輸出。可以看到閉環系統中誤差可降到1mV *311=0.331V之內（1mV為error波形的幅值，311為電壓標幺化基準值）。

參考資料1：Effects of Discretization Methods on the Performance of Resonant Controllers, Alcjandro G. Ycpcs, IEEE transactions on Power Electronics

參考資料2：PID控制器的數字實現及C語法講解

參考資料3：比例諧振控制的一種實現（含代碼）

參考資料4：采用比例諧振控制器的逆變器_葉禮清

原文鏈接：

https://blog.csdn.net/qq_27158179/article/details/82739641