很多人認為,算法是數學的內容,學起來特別麻煩。我們不能認為這種觀點是錯誤的。但是我們也知道,軟件是一種復合的技術,如果一個人只知道算法,但是不能用編程語言很好地實現,那么再優秀的算法也不能發揮作用。
有一次,一個人問我:
“你寫的都是小兒科的東西,幾十行代碼就能搞定,能不能整一點高深的算法?”
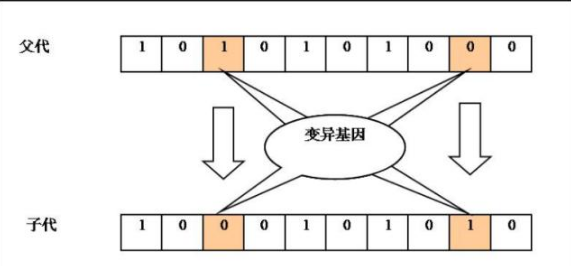
我反問他什么是他所理解的高深的算法,他答復說:“像遺傳算法、蟻群算法之類的。”于是我給了他一個遺傳算法求解0-1背包問題的例子,并告訴他,這也就是幾十行代碼的算法,怎么理解成是高深的算法?他剛開始不承認這是遺傳算法,直到我給了他Denis Cormier公開在北卡羅來納州立大學服務器上的遺傳算法的源代碼后,他才相信他一直認為深不可測的遺傳算法的原理原來是這么簡單。
還有一個人直言“用三個水桶等分8升水”之類的問題根本就稱不上算法,他認為像“阿法狗”那樣的人工智能才算是算法。我告訴他計算機下棋的基本理論就是博弈樹,或者再加一個專家系統。但是他認為博弈樹也是很高深的算法,于是我給了他一個井字棋游戲,并告訴他,這就是博弈樹搜索算法,非常智能,你絕對戰勝不了它(因為井字棋游戲很簡單,這個算法會把所有的狀態都搜索完)。我相信他一定很震驚,因為這個算法也不超過100行代碼。
對于上面提到的例子,我覺得主要原因在于大家對算法的理解有差異,很多人對算法的理解太片面,很多人覺得只有名字里包含“XX算法”之類的東西才是算法。而我認為算法的本質是解決問題,只要是能解決問題的代碼就是算法。
一個人只有有了很好的計算機知識和數學知識,才能在算法的學習上不斷進步。不管算法都么簡單,都要自己親手實踐,只有不斷認識錯誤、不斷發現錯誤,才能不斷提高自己的編程能力,不斷提高自己的業務水平。
其實任何算法都有自己的應用環境和應用場景,沒有算法可以適用于所有的場景。這一點希望大家明白。同時,我們也要清楚復雜的算法都是由普通的算法構成的,沒有普通的算法就沒有復雜的算法可言,所以復雜變簡單,由大化小,這就是算法分治遞歸的基本思想。
我們可以下面一個數組查找的函數說起。一句一句講起,首先我們開始從最簡單的函數構造開始:
1.intfind(intarray[],intlength,intvalue)
2.{
3.intindex=0;
4.returnindex;
5.}
這里看到,查找函數只是一個普通的函數,那么首先需要判斷的就是參數的合法性:
2.{
3.intarray[10]={0};
4.assert(FALSE==find(NULL,10,10));
5.assert(FALSE==find(array,0,10));
6.}
這里可以看到,我們沒有判斷參數的合法性,那么原來的查找函數應該怎么修改呢?
1.intfind(intarray[],intlength,intvalue)
2.{
3.if(NULL==array||0==length)
4.returnFALSE;
5.
6.intindex=0;
7.returnindex;
8.}
看到上面的代碼,說明我們的已經對入口參數進行判斷了。那么下面就要開始寫代碼了。
1.intfind(intarray[],intlength,intvalue)
2.{
3.if(NULL==array||0==length)
4.returnFALSE;
5.
6.intindex=0;
7.for(;index
8.if(value==array[index])
9.returnindex;
10.}
11.
12.returnFALSE;
13.}
上面的代碼已經接近完整了,那么測試用例又該怎么編寫呢?
1.staticvoidtest2()
2.{
3.intarray[10]={1,2};
4.assert(0==find(array,10,1));
5.assert(FALSE==find(array,10,10));
6.}
運行完所有的測試用例后,我們看看對原來的代碼有沒有什么可以優化的地方。其實,我們可以把數組轉變成指針。
1.intfind(intarray[],intlength,intvalue)
2.{
3.if(NULL==array||0==length)
4.returnFALSE;
5.
6.int*start=array;
7.int*end=array+length;
8.while(start
9.if(value==*start)
10.return((int)start-(int)array)/(sizeof(int));
11.start++;
12.}
13.
14.returnFALSE;
15.}
如果上面的代碼參數必須是通用的數據類型呢?
1.template
2.intfind(typearray[],intlength,typevalue)
3.{
4.if(NULL==array||0==length)
5.returnFALSE;
6.
7.type*start=array;
8.type*end=array+length;
9.while(start
10.if(value==*start)
11.return((int)start-(int)array)/(sizeof(type));
12.start++;
13.}
14.
15.returnFALSE;
16.}
此時,測試用例是不是也需要重新修改呢?
1.staticvoidtest1()
2.{
3.intarray[10]={0};
4.assert(FALSE==find
5.assert(FALSE==find
6.}
7.
8.staticvoidtest2()
9.{
10.intarray[10]={1,2};
11.assert(0==find
12.assert(FALSE==find
13.}
最后,我們總結一下:
(1)我們的算法需要測試用例的驗證
(2)任何的優化都要建立在測試的基礎之上
(3)測試和代碼的編寫要同步進行
(4)算法的成功運行時一步一步進行得,每一步的成功必須確立在原有的成功之上
-
遺傳算法
+關注
關注
0文章
237瀏覽量
20632
原文標題:算法又難又神秘?你大錯特錯!
文章出處:【微信號:weixin21ic,微信公眾號:21ic電子網】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 深不可測的遺傳算法的原理原來是這么簡單
深不可測的遺傳算法的原理原來是這么簡單










評論