序言
本文盡可能的不涉及到繁雜的數(shù)學(xué)公式,把面試中常問的模型核心點,用比較通俗易懂但又不是專業(yè)性的語言進行描述。
希望可以幫助大家在找工作時提綱挈領(lǐng)的復(fù)習(xí)最核心的內(nèi)容,或是在準(zhǔn)備的過程中抓住每個模型的重點。
實戰(zhàn)環(huán)境說明:
Python 2.7;
Sklearn 0.19.0;
graphviz 0.8.1 決策樹可視化。
一、決策樹
▌1.1 原理
顧名思義,決策樹就是用一棵樹來表示我們的整個決策過程。這棵樹可以是二叉樹(比如 CART 只能是二叉樹),也可以是多叉樹(比如 ID3、C4.5 可以是多叉樹或二叉樹)。
根節(jié)點包含整個樣本集,每個葉節(jié)都對應(yīng)一個決策結(jié)果(注意,不同的葉節(jié)點可能對應(yīng)同一個決策結(jié)果),每一個內(nèi)部節(jié)點都對應(yīng)一次決策過程或者說是一次屬性測試。從根節(jié)點到每個葉節(jié)點的路徑對應(yīng)一個判定測試序列。
舉個例子:
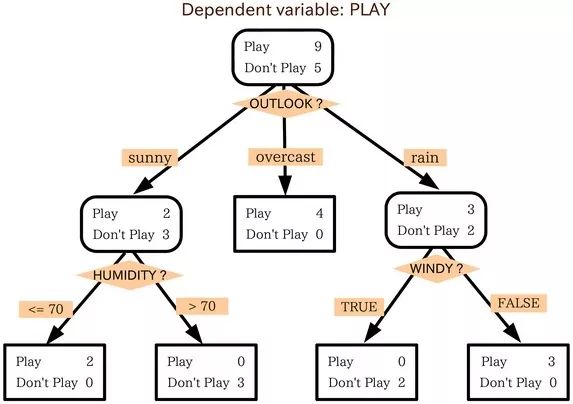
就像上面這個例子,訓(xùn)練集由三個特征:outlook(天氣),humidity(濕度),windy(是否有風(fēng))。
那么我們該如何選擇特征對訓(xùn)練集進行劃分那?連續(xù)型特征(比如濕度)劃分的閾值又是如何確定的?
決策樹的生成就是不斷的選擇最優(yōu)的特征對訓(xùn)練集進行劃分,是一個遞歸的過程。遞歸返回的條件有三種:
(1)當(dāng)前節(jié)點包含的樣本屬于同一類別,無需劃分;
(2)當(dāng)前屬性集為空,或所有樣本在屬性集上取值相同,無法劃分;
(3)當(dāng)前節(jié)點包含樣本集合為空,無法劃分。
1.2 ID3、C4.5、CART
這三個是非常著名的決策樹算法。簡單粗暴來說,ID3 使用信息增益作為選擇特征的準(zhǔn)則;C4.5 使用信息增益比作為選擇特征的準(zhǔn)則;CART 使用 Gini 指數(shù)作為選擇特征的準(zhǔn)則。
ID3
熵表示的是數(shù)據(jù)中包含的信息量大小。熵越小,數(shù)據(jù)的純度越高,也就是說數(shù)據(jù)越趨于一致,這是我們希望的劃分之后每個子節(jié)點的樣子。
信息增益 = 劃分前熵 - 劃分后熵。信息增益越大,則意味著使用屬性 a 來進行劃分所獲得的 “純度提升” 越大 **。也就是說,用屬性 a 來劃分訓(xùn)練集,得到的結(jié)果中純度比較高。
ID3 僅僅適用于二分類問題。ID3 僅僅能夠處理離散屬性。
C4.5
C4.5 克服了 ID3 僅僅能夠處理離散屬性的問題,以及信息增益偏向選擇取值較多特征的問題,使用信息增益比來選擇特征。信息增益比 = 信息增益 / 劃分前熵選擇信息增益比最大的作為最優(yōu)特征。
C4.5 處理連續(xù)特征是先將特征取值排序,以連續(xù)兩個值中間值作為劃分標(biāo)準(zhǔn)。嘗試每一種劃分,并計算修正后的信息增益,選擇信息增益最大的分裂點作為該屬性的分裂點。
CART
CART 與 ID3,C4.5 不同之處在于 CART 生成的樹必須是二叉樹。也就是說,無論是回歸還是分類問題,無論特征是離散的還是連續(xù)的,無論屬性取值有多個還是兩個,內(nèi)部節(jié)點只能根據(jù)屬性值進行二分。
CART 的全稱是分類與回歸樹。從這個名字中就應(yīng)該知道,CART 既可以用于分類問題,也可以用于回歸問題。
回歸樹中,使用平方誤差最小化準(zhǔn)則來選擇特征并進行劃分。每一個葉子節(jié)點給出的預(yù)測值,是劃分到該葉子節(jié)點的所有樣本目標(biāo)值的均值,這樣只是在給定劃分的情況下最小化了平方誤差。
要確定最優(yōu)化分,還需要遍歷所有屬性,以及其所有的取值來分別嘗試劃分并計算在此種劃分情況下的最小平方誤差,選取最小的作為此次劃分的依據(jù)。由于回歸樹生成使用平方誤差最小化準(zhǔn)則,所以又叫做最小二乘回歸樹。
分類樹種,使用 Gini 指數(shù)最小化準(zhǔn)則來選擇特征并進行劃分;
Gini 指數(shù)表示集合的不確定性,或者是不純度。基尼指數(shù)越大,集合不確定性越高,不純度也越大。這一點和熵類似。另一種理解基尼指數(shù)的思路是,基尼指數(shù)是為了最小化誤分類的概率。
▌1.3 信息增益 vs 信息增益比
之所以引入了信息增益比,是由于信息增益的一個缺點。那就是:信息增益總是偏向于選擇取值較多的屬性。信息增益比在此基礎(chǔ)上增加了一個罰項,解決了這個問題。
▌1.4 Gini 指數(shù) vs 熵
既然這兩個都可以表示數(shù)據(jù)的不確定性,不純度。那么這兩個有什么區(qū)別那?
Gini 指數(shù)的計算不需要對數(shù)運算,更加高效;
Gini 指數(shù)更偏向于連續(xù)屬性,熵更偏向于離散屬性。
▌1.5 剪枝
決策樹算法很容易過擬合(overfitting),剪枝算法就是用來防止決策樹過擬合,提高泛華性能的方法。
剪枝分為預(yù)剪枝與后剪枝。
預(yù)剪枝是指在決策樹的生成過程中,對每個節(jié)點在劃分前先進行評估,若當(dāng)前的劃分不能帶來泛化性能的提升,則停止劃分,并將當(dāng)前節(jié)點標(biāo)記為葉節(jié)點。
后剪枝是指先從訓(xùn)練集生成一顆完整的決策樹,然后自底向上對非葉節(jié)點進行考察,若將該節(jié)點對應(yīng)的子樹替換為葉節(jié)點,能帶來泛化性能的提升,則將該子樹替換為葉節(jié)點。
那么怎么來判斷是否帶來泛化性能的提升那?最簡單的就是留出法,即預(yù)留一部分?jǐn)?shù)據(jù)作為驗證集來進行性能評估。
▌1.6 總結(jié)
決策樹算法主要包括三個部分:特征選擇、樹的生成、樹的剪枝。常用算法有 ID3、C4.5、CART。
特征選擇。特征選擇的目的是選取能夠?qū)τ?xùn)練集分類的特征。特征選擇的關(guān)鍵是準(zhǔn)則:信息增益、信息增益比、Gini 指數(shù);
決策樹的生成。通常是利用信息增益最大、信息增益比最大、Gini 指數(shù)最小作為特征選擇的準(zhǔn)則。從根節(jié)點開始,遞歸的生成決策樹。相當(dāng)于是不斷選取局部最優(yōu)特征,或?qū)⒂?xùn)練集分割為基本能夠正確分類的子集;
決策樹的剪枝。決策樹的剪枝是為了防止樹的過擬合,增強其泛化能力。包括預(yù)剪枝和后剪枝。
二、隨機森林(Random Forest)
要說隨機森林就要先說 Bagging,要說 Bagging 就要先說集成學(xué)習(xí)。
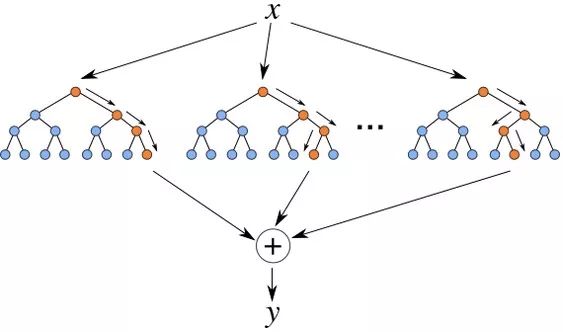
▌2.1 集成學(xué)習(xí)方法
集成學(xué)習(xí)(ensemble learning)通過構(gòu)建并組合多個學(xué)習(xí)器來完成學(xué)習(xí)任務(wù)。集成學(xué)習(xí)通過將多個學(xué)習(xí)器進行結(jié)合,常獲得比單一學(xué)習(xí)器顯著優(yōu)越的泛化性能。
根據(jù)個體學(xué)習(xí)器是否是同類型的學(xué)習(xí)器(由同一個算法生成,比如 C4.5,BP 等),分為同質(zhì)和異質(zhì)。同質(zhì)的個體學(xué)習(xí)器又叫做基學(xué)習(xí)器,而異質(zhì)的個體學(xué)習(xí)器則直接成為個體學(xué)習(xí)器。
原則:要獲得比單一學(xué)習(xí)器更好的性能,個體學(xué)習(xí)器應(yīng)該好而不同。即個體學(xué)習(xí)器應(yīng)該具有一定的準(zhǔn)確性,不能差于弱學(xué)習(xí)器,并且具有多樣性,即學(xué)習(xí)器之間有差異。
根據(jù)個體學(xué)習(xí)器的生成方式,目前集成學(xué)習(xí)分為兩大類:
個體學(xué)習(xí)器之間存在強依賴關(guān)系、必須串行生成的序列化方法。代表是 Boosting;
個體學(xué)習(xí)器之間不存在強依賴關(guān)系、可同時生成的并行化方法。代表是 Bagging 和隨機森林(Random Forest)。
▌2.2 Bagging
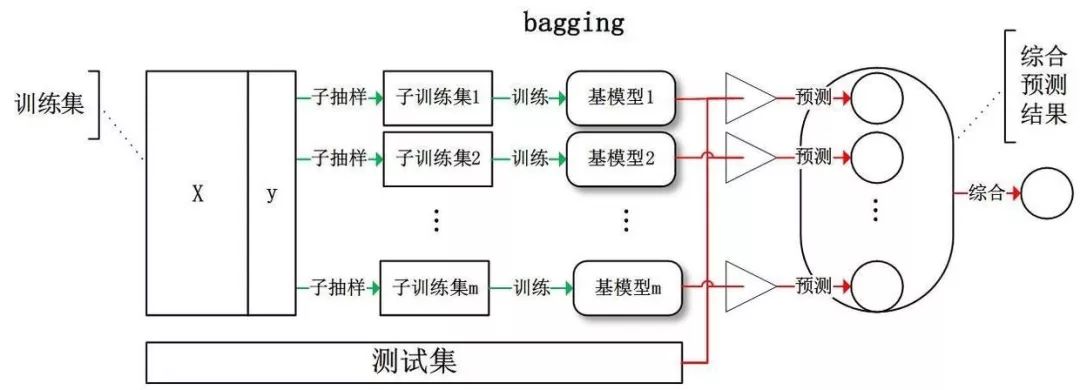
前面提到,想要集成算法獲得性能的提升,個體學(xué)習(xí)器應(yīng)該具有獨立性。雖然 “獨立” 在現(xiàn)實生活中往往無法做到,但是可以設(shè)法讓基學(xué)習(xí)器盡可能的有較大的差異。
Bagging 給出的做法就是對訓(xùn)練集進行采樣,產(chǎn)生出若干個不同的子集,再從每個訓(xùn)練子集中訓(xùn)練一個基學(xué)習(xí)器。由于訓(xùn)練數(shù)據(jù)不同,我們的基學(xué)習(xí)器可望具有較大的差異。
Bagging 是并行式集成學(xué)習(xí)方法的代表,采樣方法是自助采樣法,用的是有放回的采樣。初始訓(xùn)練集中大約有 63.2% 的數(shù)據(jù)出現(xiàn)在采樣集中。
Bagging 在預(yù)測輸出進行結(jié)合時,對于分類問題,采用簡單投票法;對于回歸問題,采用簡單平均法。
Bagging 優(yōu)點:
高效。Bagging 集成與直接訓(xùn)練基學(xué)習(xí)器的復(fù)雜度同階;
Bagging 能不經(jīng)修改的適用于多分類、回歸任務(wù);
包外估計。使用剩下的樣本作為驗證集進行包外估計(out-of-bag estimate)。
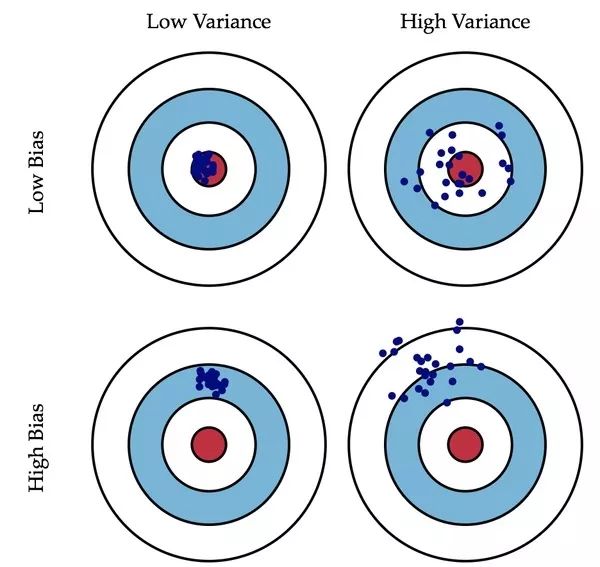
Bagging 主要關(guān)注降低方差。(low variance)
▌2.3 隨機森林(Random Forest)
2.3.1 原理
隨機森林(Random Forest)是 Bagging 的一個變體。Ramdon Forest 在以決策樹為基學(xué)習(xí)器構(gòu)建 Bagging 集成的基礎(chǔ)上,進一步在決策樹的訓(xùn)練過程中引入隨機屬性選擇。
原來決策樹從所有屬性中,選擇最優(yōu)屬性。Ramdom Forest 的每一顆決策樹中的每一個節(jié)點,先從該節(jié)點的屬性集中隨機選擇 K 個屬性的子集,然后從這個屬性子集中選擇最優(yōu)屬性進行劃分。
K 控制了隨機性的引入程度,是一個重要的超參數(shù)。
預(yù)測:
分類:簡單投票法;
回歸:簡單平均法。
2.3.2 優(yōu)缺點
優(yōu)點:
由于每次不再考慮全部的屬性,而是一個屬性子集,所以相比于 Bagging 計算開銷更小,訓(xùn)練效率更高;
由于增加了屬性的擾動,隨機森林中基學(xué)習(xí)器的性能降低,使得在隨機森林在起始時候性能較差,但是隨著基學(xué)習(xí)器的增多,隨機森林通常會收斂于更低的泛化誤差,相比于 Bagging;
兩個隨機性的引入,使得隨機森林不容易陷入過擬合,具有很好的抗噪聲能力;
對數(shù)據(jù)的適應(yīng)能力強,可以處理離散和連續(xù)的,無需要規(guī)范化;
可以得到變量的重要性, 基于 oob 誤分類率和基于 Gini 系數(shù)的變化。
缺點:
在噪聲較大的時候容易過擬合。
三、AdaBoost
AdaBoost 是 Boosting 的代表,前面我們提到 Boosting 是集成學(xué)習(xí)中非常重要的一類串行化學(xué)習(xí)方法。
▌3.1 Boosting
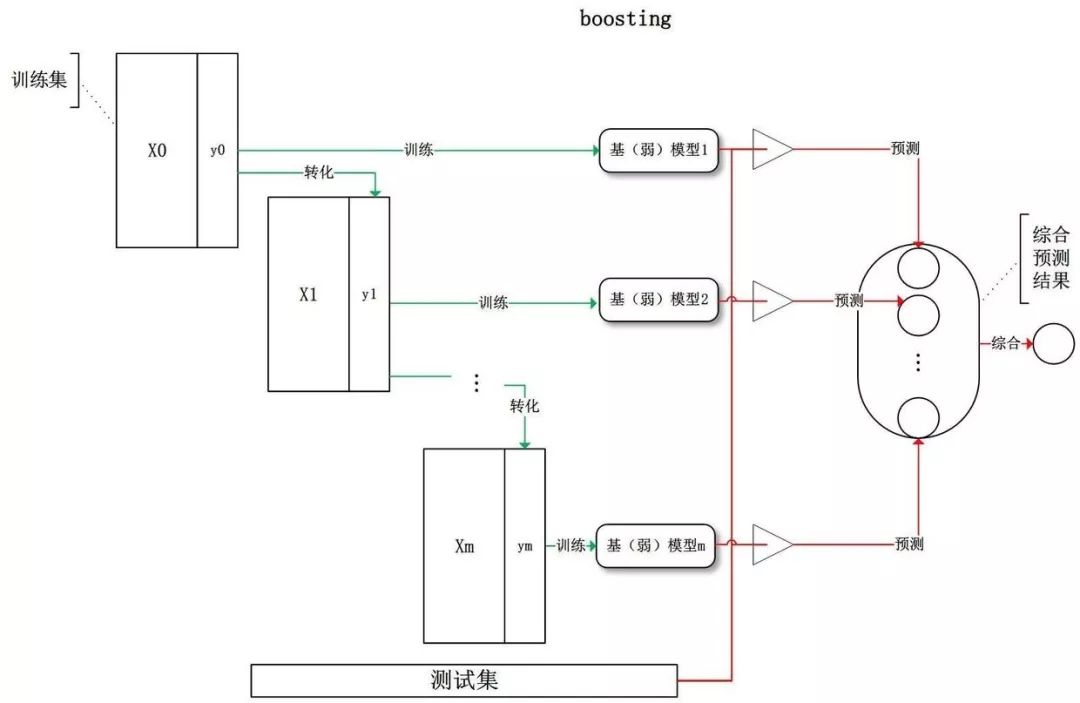
Boosting 是指個體學(xué)習(xí)器之間存在強依賴關(guān)系,必須串行序列化生成的集成學(xué)習(xí)方法。他的思想來源是三個臭皮匠頂個諸葛亮。Boosting 意為提升,意思是希望將每個弱學(xué)習(xí)器提升為強學(xué)習(xí)器。
工作機制如下:
先從初始訓(xùn)練集中學(xué)習(xí)一個基學(xué)習(xí)器;
根據(jù)基學(xué)習(xí)器的表現(xiàn)對訓(xùn)練樣本分布進行調(diào)整,使得先前基學(xué)習(xí)器做錯的訓(xùn)練樣本在后續(xù)收到更多關(guān)注;
基于調(diào)整后的樣本分布來訓(xùn)練下一個基學(xué)習(xí)器;
如此反復(fù),直到基學(xué)習(xí)器數(shù)目達到 T,最終將這 T 個基學(xué)習(xí)器進行加權(quán)結(jié)合。
對訓(xùn)練樣本分布調(diào)整,主要是通過增加誤分類樣本的權(quán)重,降低正確分類樣本的權(quán)重。
Boosting 關(guān)注的主要是降低偏差。(low bias)
▌3.2 AdaBoost 原理
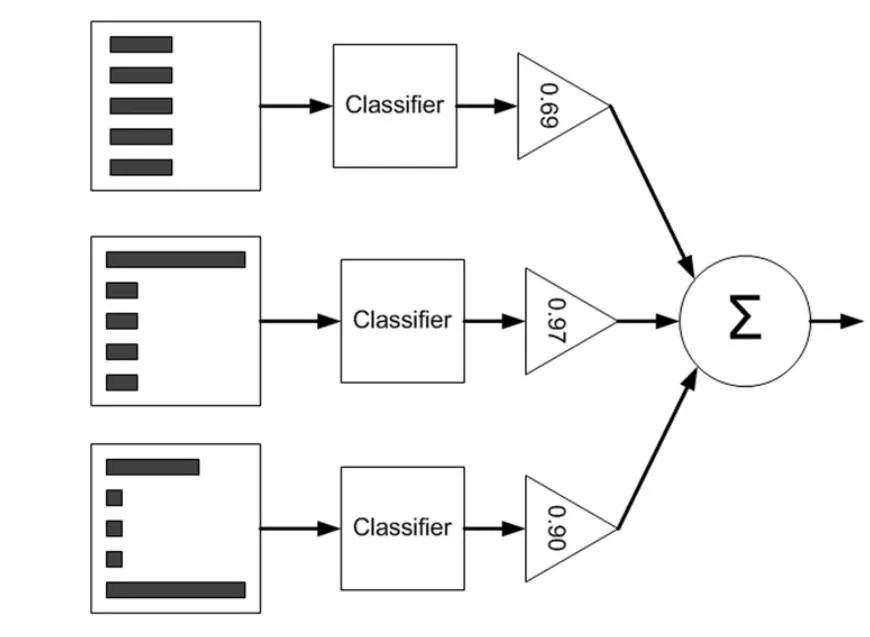
面臨兩個問題:
(1)在每一輪,如何改變訓(xùn)練數(shù)據(jù)的概率分布或者權(quán)值分布。(也可以重采樣,但是 AdaBoost 沒這么做);
(2)如何將弱分類器組合成強分類器。
AdaBoost 的做法:
(1)提高那些被前一輪弱分類器錯誤分類樣本的權(quán)值,降低那些被正確分類的樣本的權(quán)值。這樣一來,那些沒有得到正確分類的數(shù)據(jù),由于其權(quán)值的加大而受到后一輪弱分類器的關(guān)注;
(2)采用加權(quán)多數(shù)表決。具體的,加大分類錯誤率低的分類器的權(quán)值,使其在表決中起較大作用,減少分類誤差率大的弱分類器的權(quán)值,使其在表決中起較小作用。
弱分類器被線性組合成為一個強分類器。
訓(xùn)練目標(biāo):
最小化指數(shù)損失函數(shù)。
三部分組成:
(1)分類器權(quán)重更新公式;
(2)樣本分布(也就是樣本權(quán)重)更新公式;
(3)加性模型。 最小化指數(shù)損失函數(shù)。
▌3.3 AdaBoost 優(yōu)缺點
優(yōu)點:
不改變所給的訓(xùn)練數(shù)據(jù),而不斷改變訓(xùn)練數(shù)據(jù)的權(quán)值分布,使得訓(xùn)練數(shù)據(jù)在基本分類器的學(xué)習(xí)中起不同的作用。這是 AdaBoost 的一個特點;
利用基本分類器的加權(quán)線性組合構(gòu)建最終分類器,是 AdaBoost 的另一個特點;
AdaBoost 被實踐證明是一種很好的防止過擬合的方法,但至今為什么至今沒從理論上證明。
缺點:
AdaBoost 只適用于二分類問題。
四、GBDT
GBDT(Gradient Boosting Decision Tree)又叫 MART(Multiple Additive Regression Tree)。是一種迭代的決策樹算法。
本文從以下幾個方面進行闡述:
Regression Decision Tree(DT);
Gradient Boosting(GB);
Shrinkage(算法的一個重要演進分支,目前大部分源碼都是基于該版本實現(xiàn));
GBDT 適用范圍;
與隨機森林的對比。
▌4.1 DT:回歸樹 Regression Decision Tree
GDBT 中的樹全部都是回歸樹,核心就是累加所有樹的結(jié)果作為最終結(jié)果。只有回歸樹的結(jié)果累加起來才是有意義的,分類的結(jié)果加是沒有意義的。
GDBT 調(diào)整之后可以用于分類問題,但是內(nèi)部還是回歸樹。
這部分和決策樹中的是一樣的,無非就是特征選擇。回歸樹用的是最小化均方誤差,分類樹是用的是最小化基尼指數(shù)(CART)
▌4.2 GB:梯度迭代 Gradient Boosting
首先 Boosting 是一種集成方法。通過對弱分類器的組合得到強分類器,他是串行的,幾個弱分類器之間是依次訓(xùn)練的。GBDT 的核心就在于,每一顆樹學(xué)習(xí)的是之前所有樹結(jié)論和的殘差。
Gradient 體現(xiàn)在:無論前面一顆樹的 cost function 是什么,是均方差還是均差,只要它以誤差作為衡量標(biāo)準(zhǔn),那么殘差向量都是它的全局最優(yōu)方向,這就是 Gradient。
▌4.3 Shrinkage
Shrinkage(縮減)是 GBDT 算法的一個重要演進分支,目前大部分的源碼都是基于這個版本的。
核心思想在于:Shrinkage 認(rèn)為每次走一小步來逼近結(jié)果的效果,要比每次邁一大步很快逼近結(jié)果的方式更容易防止過擬合。
也就是說,它不信任每次學(xué)習(xí)到的殘差,它認(rèn)為每棵樹只學(xué)習(xí)到了真理的一小部分,累加的時候只累加一小部分,通過多學(xué)習(xí)幾棵樹來彌補不足。
具體的做法就是:仍然以殘差作為學(xué)習(xí)目標(biāo),但是對于殘差學(xué)習(xí)出來的結(jié)果,只累加一小部分(step* 殘差)逐步逼近目標(biāo),step 一般都比較小 0.01-0.001, 導(dǎo)致各個樹的殘差是漸變而不是陡變的。
本質(zhì)上,Shrinkage 為每一顆樹設(shè)置了一個 weight,累加時要乘以這個 weight,但和 Gradient 沒有關(guān)系。
這個 weight 就是 step。跟 AdaBoost 一樣,Shrinkage 能減少過擬合也是經(jīng)驗證明的,目前還沒有理論證明。
▌4.4 GBDT 適用范圍
GBDT 可以適用于回歸問題(線性和非線性),相對于 logistic regression 僅能用于線性回歸,GBDT 適用面更廣;
GBDT 也可用于二分類問題(設(shè)定閾值,大于為正,否則為負(fù))和多分類問題。
▌4.5 GBDT 和隨機森林
GBDT 和隨機森林的相同點:
都是由多棵樹組成;
最終的結(jié)果都由多棵樹共同決定。
GBDT 和隨機森林的不同點:
組成隨機森林的可以是分類樹、回歸樹;組成 GBDT 只能是回歸樹;
組成隨機森林的樹可以并行生成(Bagging);GBDT 只能串行生成(Boosting);
對于最終的輸出結(jié)果而言,隨機森林使用多數(shù)投票或者簡單平均;而 GBDT 則是將所有結(jié)果累加起來,或者加權(quán)累加起來;
隨機森林對異常值不敏感,GBDT 對異常值非常敏感;
隨機森林對訓(xùn)練集一視同仁權(quán)值一樣,GBDT 是基于權(quán)值的弱分類器的集成;
隨機森林通過減小模型的方差提高性能,GBDT 通過減少模型偏差提高性能。
TIP
1. GBDT 相比于決策樹有什么優(yōu)點
泛化性能更好!GBDT 的最大好處在于,每一步的殘差計算其實變相的增大了分錯樣本的權(quán)重,而已經(jīng)分對的樣本則都趨向于 0。這樣后面就更加專注于那些分錯的樣本。
2. Gradient 體現(xiàn)在哪里?
可以理解為殘差是全局最優(yōu)的絕對方向,類似于求梯度。
3. re-sample
GBDT 也可以在使用殘差的同時引入 Bootstrap re-sampling,GBDT 多數(shù)實現(xiàn)版本中引入了這個選項,但是是否一定使用有不同的看法。
原因在于 re-sample 導(dǎo)致的隨機性,使得模型不可復(fù)現(xiàn),對于評估提出一定的挑戰(zhàn),比如很難確定性能的提升是由于 feature 的原因還是 sample 的隨機因素。
五、Logistic 回歸
LR 原理;
參數(shù)估計;
LR 的正則化;
為什么 LR 能比線性回歸好?
LR 與 MaxEnt 的關(guān)系。
▌5.1 LR 模型原理
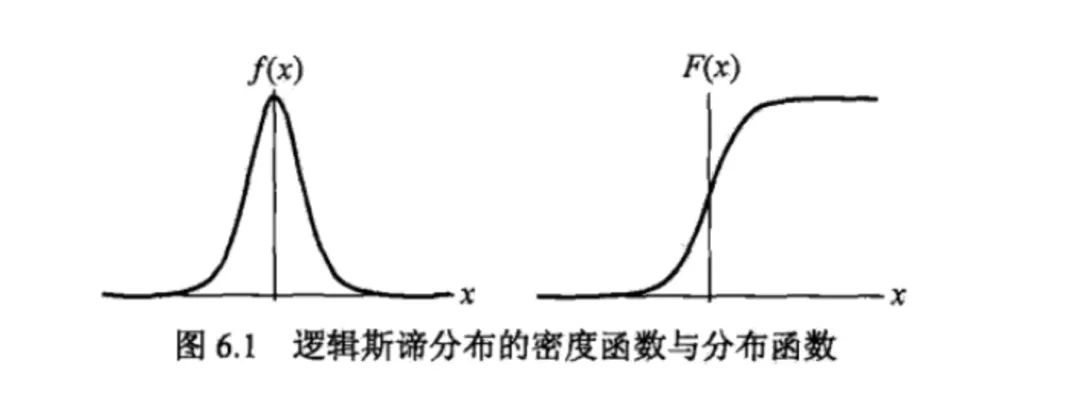
首先必須給出 Logistic 分布:
u 是位置參數(shù),r 是形狀參數(shù)。對稱點是 (u,1/2),r 越小,函數(shù)在 u 附近越陡峭。
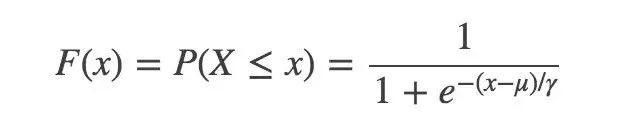
然后,二分類 LR 模型,是參數(shù)化的 logistic 分布,使用條件概率來表示:
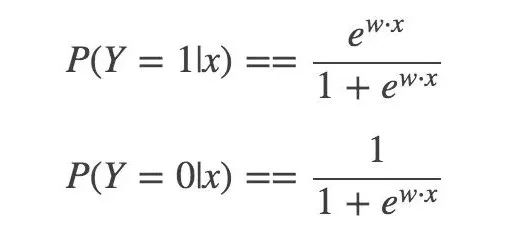
然后,一個事件的幾率(odds):指該事件發(fā)生與不發(fā)生的概率比值:
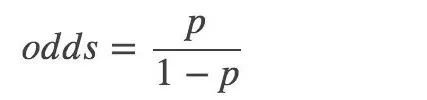
對數(shù)幾率:
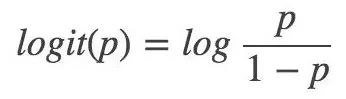
那么對于邏輯回歸而言,Y=1 的對數(shù)幾率就是:
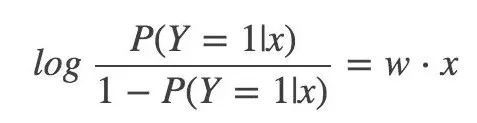
最終,輸出 Y=1 的對數(shù)幾率是輸入 x 的線性函數(shù)表示的模型,這就是邏輯回歸模型。
▌5.2 參數(shù)估計
在統(tǒng)計學(xué)中,常常使用極大似然估計法來估計參數(shù)。即找到一組參數(shù),使得在這組參數(shù)下,我們數(shù)據(jù)的似然度(概率)最大。
似然函數(shù):
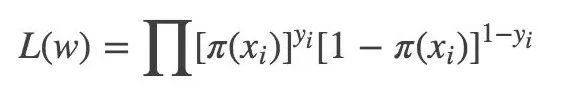
對數(shù)似然函數(shù):
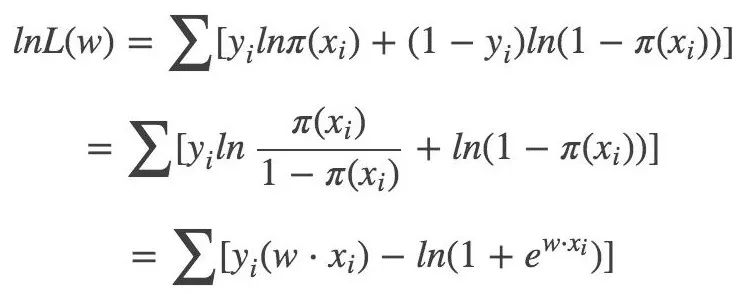
對應(yīng)的損失函數(shù):
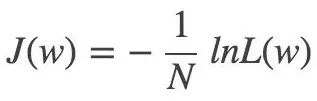
▌5.3 最優(yōu)化方法
邏輯回歸模型的參數(shù)估計中,最后就是對 J(W) 求最小值。這種不帶約束條件的最優(yōu)化問題,常用梯度下降或牛頓法來解決。
使用梯度下降法求解邏輯回歸參數(shù)估計
求 J(W) 梯度:g(w):
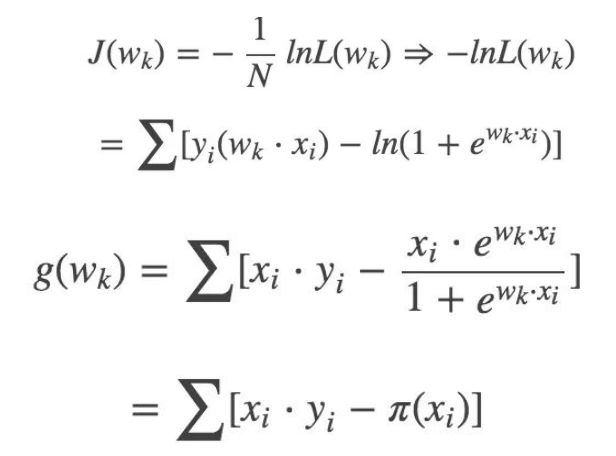
更新 Wk:
$$ W_{k+1} = W_k - \lambda*g(W_k) $$
▌5.4 正則化
正則化為了解決過擬合問題。分為 L1 和 L2 正則化。主要通過修正損失函數(shù),加入模型復(fù)雜性評估;
正則化是符合奧卡姆剃刀原理:在所有可能的模型中,能夠很好的解釋已知數(shù)據(jù)并且十分簡單的才是最好的模型。
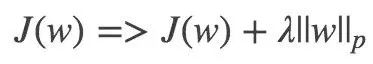
p 表示范數(shù),p=1 和 p=2 分別應(yīng)用 L1 和 L2 正則。
L1 正則化。向量中各元素絕對值之和。又叫做稀疏規(guī)則算子(Lasso regularization)。關(guān)鍵在于能夠?qū)崿F(xiàn)特征的自動選擇,參數(shù)稀疏可以避免非必要的特征引入的噪聲;
L2 正則化。使得每個元素都盡可能的小,但是都不為零。在回歸里面,有人把他的回歸叫做嶺回歸(Ridge Regression),也有人叫他 “權(quán)值衰減”(weight decay)。
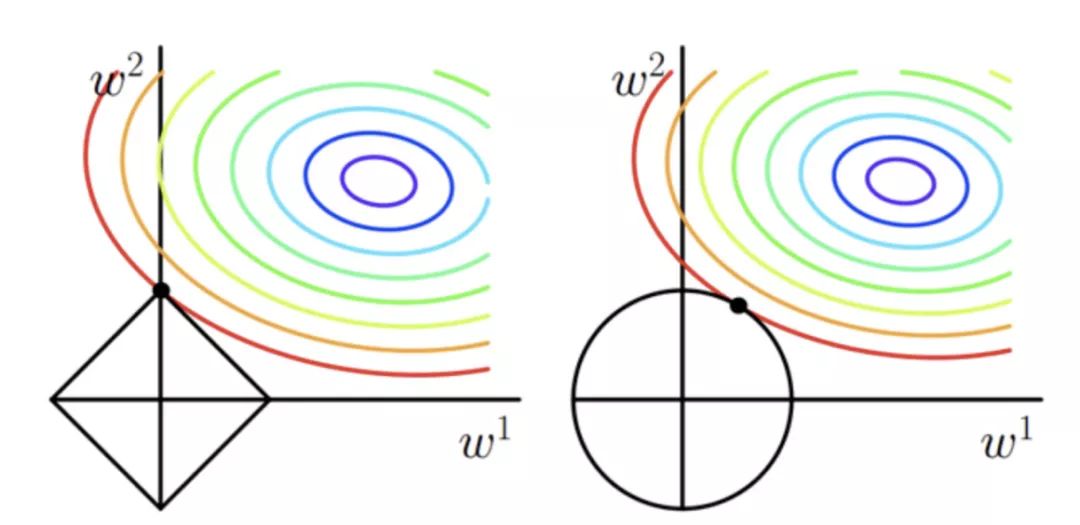
一句話總結(jié)就是:L1 會趨向于產(chǎn)生少量的特征,而其他的特征都是 0,而 L2 會選擇更多的特征,這些特征都會接近于 0.
▌5.5 邏輯回歸 vs 線性回歸
首先,邏輯回歸比線性回歸要好。
兩者都屬于廣義線性模型。
線性回歸優(yōu)化目標(biāo)函數(shù)用的最小二乘法,而邏輯回歸用的是最大似然估計。邏輯回歸只是在線性回歸的基礎(chǔ)上,將加權(quán)和通過 sigmoid 函數(shù),映射到 0-1 范圍內(nèi)空間。
線性回歸在整個實數(shù)范圍內(nèi)進行預(yù)測,敏感度一致,而分類范圍,需要在 [0,1]。而邏輯回歸就是一種減小預(yù)測范圍,將預(yù)測值限定為 [0,1] 間的一種回歸模型。
邏輯曲線在 z=0 時,十分敏感,在 z>>0 或 z<<0 處,都不敏感,將預(yù)測值限定為 (0,1)。邏輯回歸的魯棒性比線性回歸要好。
▌5.6 邏輯回歸模型 vs 最大熵模型 MaxEnt
簡單粗暴的說:邏輯回歸跟最大熵模型沒有本質(zhì)區(qū)別。邏輯回歸是最大熵對應(yīng)為二類時的特殊情況,也就是說,當(dāng)邏輯回歸擴展為多類別的時候,就是最大熵模型。
最大熵原理:學(xué)習(xí)概率模型的時候,在所有可能的概率模型(分布)中,熵最大的模型是最好的模型。
六、SVM 支持向量機
雖然咱們的目標(biāo)是盡可能的不涉及到公式,但是提到 SVM 就沒有辦法不涉及到公式推導(dǎo),因為面試中只要問到 SVM,最基本也是最難的問題就是:SVM 的對偶問題數(shù)學(xué)公式推導(dǎo)。
所以想學(xué)好機器學(xué)習(xí),還是要塌下心來,不僅僅要把原理的核心思想掌握了,公式推導(dǎo)也要好好學(xué)習(xí)才行。
▌6.1 SVM 原理
簡單粗暴的說:SVM 的思路就是找到一個超平面將數(shù)據(jù)集進行正確的分類。對于在現(xiàn)有維度不可分的數(shù)據(jù),利用核函數(shù)映射到高緯空間使其線性可分。
支持向量機 SVM 是一種二分類模型。它的基本模型是定義在特征空間上的間隔最大的線性分類器,間隔最大使它有別于感知機。SVM 的學(xué)習(xí)策略是間隔最大化,可形式化為求解凸二次規(guī)劃問題。
SVM 分為:
線性可分支持向量機。當(dāng)訓(xùn)練數(shù)據(jù)線性可分時,通過硬間隔最大化,學(xué)習(xí)到的一個線性分類器;
線性支持向量機。當(dāng)訓(xùn)練數(shù)據(jù)近似線性可分時,通過軟間隔最大化,學(xué)習(xí)到的一個線性分類器;
非線性支持向量機。當(dāng)訓(xùn)練數(shù)據(jù)線性不可分,通過使用核技巧及軟間隔最大化,學(xué)習(xí)非線性支持向量機。
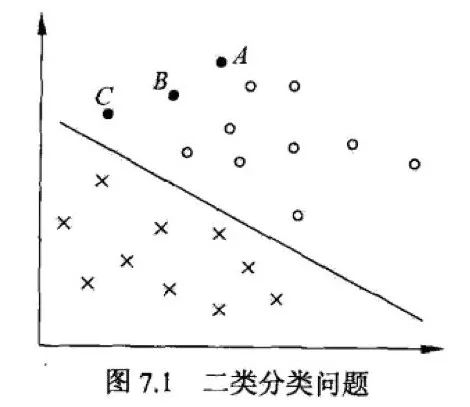
上圖中,X 表示負(fù)例,O 表示正例。此時的訓(xùn)練數(shù)據(jù)可分,線性可分支持向量機對應(yīng)著將兩類數(shù)據(jù)正確劃分并且間隔最大的直線。
6.1.1 支持向量與間隔
支持向量:在線性可分的情況下,訓(xùn)練數(shù)據(jù)樣本集中的樣本點中與分離超平面距離最近的樣本點的實例稱為支持向量(support vector)。
函數(shù)間隔定義如下:

yi 表示目標(biāo)值,取值為 +1、-1. 函數(shù)間隔雖然可以表示分類預(yù)測的準(zhǔn)確性以及確信度。但是有個不好的性質(zhì):只要成倍的改變 W 和 B,雖然此時的超平面并沒有改變,但是函數(shù)間隔會變大。
所以我們想到了對超平面的法向量 W 施加一些約束,比如規(guī)范化,使得間隔確定,這就引出了幾何間隔:

支持向量學(xué)習(xí)的基本思想就是求解能夠正確劃分訓(xùn)練數(shù)據(jù)集并且?guī)缀伍g隔最大的分類超平面。
6.1.2 對偶問題
為了求解線性可分支持向量機的最優(yōu)化問題:
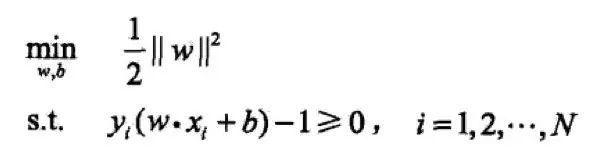
將它作為原始最優(yōu)化問題,應(yīng)用拉格朗日對偶性,通過求解對偶問題得到原始問題的最優(yōu)解,這就是線性可分支持向量機的對偶算法。
本來的算法也可以求解 SVM,但是之所以要用對偶問題來求解,優(yōu)點是:
一是對偶問題往往更容易求解;
二是自然引入核函數(shù),進而推廣到非線性分類問題。
說點題外話,這也是面試中會被問到的一個問題:原始問題既然可以求解,為什么還要轉(zhuǎn)換為對偶問題。
答案就是上述這兩點。由于篇幅的愿意,此處就不在展開數(shù)學(xué)公式的推導(dǎo)了,大家可以參考《機器學(xué)習(xí)》與《統(tǒng)計學(xué)習(xí)方法》。
6.1.3 核函數(shù)
對于在原始空間中不可分的問題,在高維空間中是線性可分的。
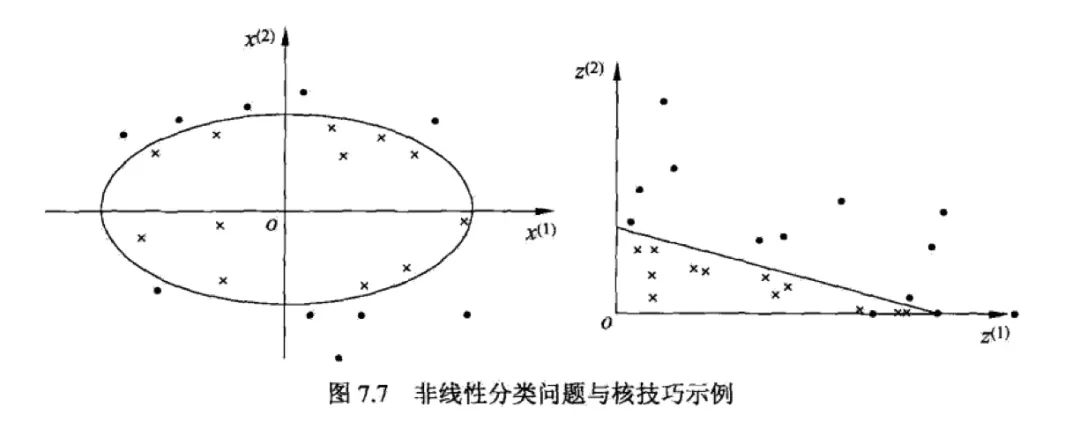
對于線性不可分的問題,使用核函數(shù)可以從原始空間映射到高緯空間,使得問題變得線性可分。核函數(shù)還可以使得在高維空間計算的內(nèi)積在低維空間中通過一個函數(shù)來完成。
常用的核函數(shù)有:高斯核、線性核、多項式核。
6.1.4 軟間隔
線性可分問題的支持向量機學(xué)習(xí)方法,對現(xiàn)行不可分訓(xùn)練數(shù)據(jù)是不適用的。所以講間隔函數(shù)修改為軟間隔,對于函數(shù)間隔,在其上加上一個松弛變量,使其滿足大于等于 1。約束條件變?yōu)椋?/p>
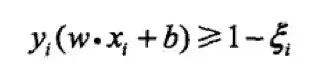
▌6.2 優(yōu)缺點
缺點:
時空開銷比較大,訓(xùn)練時間長;
核函數(shù)的選取比較難,主要靠經(jīng)驗。
優(yōu)點:
在小訓(xùn)練集上往往得到比較好的結(jié)果;
使用核函數(shù)避開了高緯空間的復(fù)雜性;
泛化能力強。
七、利用 sklearn 進行實戰(zhàn)
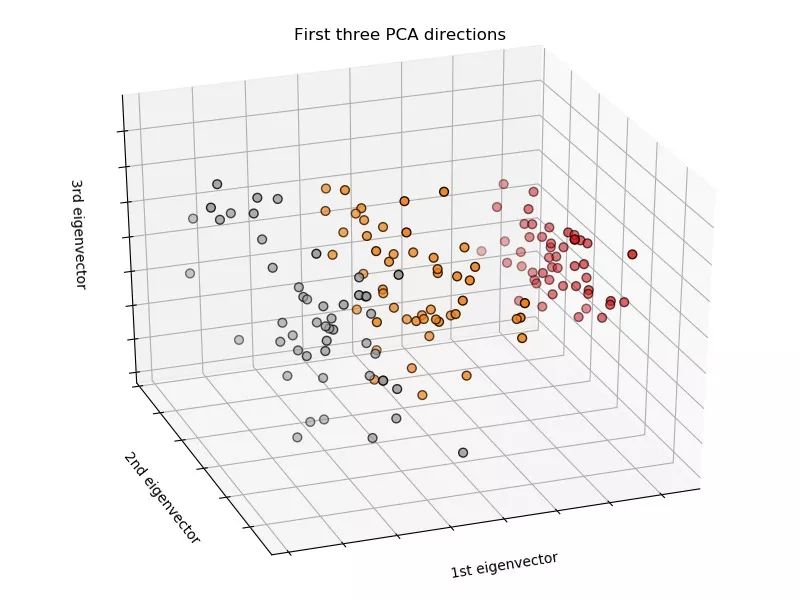
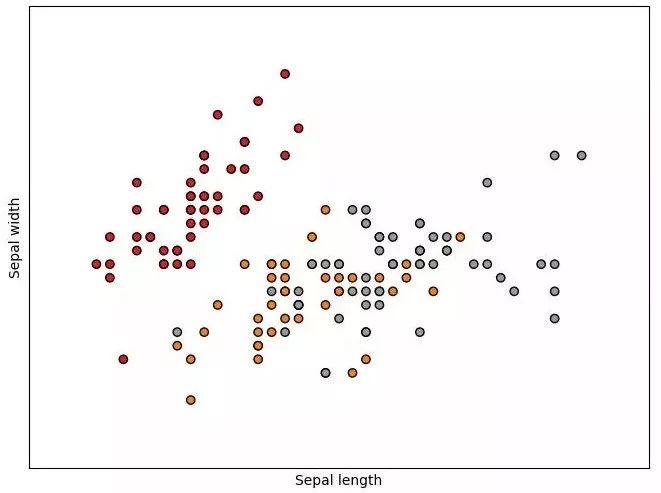
使用 sklearn 用決策樹來進行鶯尾花數(shù)據(jù)集的劃分問題。代碼上沒有固定隨機種子,所以每次運行的結(jié)果會稍有不同。
數(shù)據(jù)集三維可視化:
在 Sepal length 和 Sepal width 二維上的可視化:



運行結(jié)果:

Decision Tree 可視化,也就是生成的決策樹:
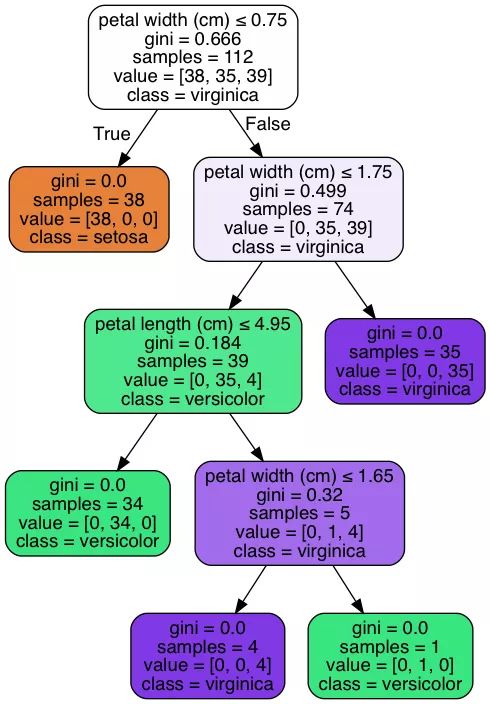
-
機器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8419瀏覽量
132675 -
決策樹
+關(guān)注
關(guān)注
3文章
96瀏覽量
13554
原文標(biāo)題:機器學(xué)習(xí)面試干貨精講
文章出處:【微信號:AI_Thinker,微信公眾號:人工智能頭條】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
精講多練MATLAB
干貨!java經(jīng)典面試套路精講視頻教程免費分享!
java基礎(chǔ):Java七大外企經(jīng)典面試精講視頻
java面試考點精講視頻教程!
面試必看:java面試考點精講視頻教程
Java面試筆試考點精講視頻教程
Java經(jīng)典面試精講視頻課程免費了!
25個機器學(xué)習(xí)面試題,你都會嗎?
開關(guān)電源控制環(huán)路精講PDF學(xué)習(xí)資料文檔電子書
人工智能工程師高頻面試題匯總——機器學(xué)習(xí)篇

【面試題】人工智能工程師高頻面試題匯總:機器學(xué)習(xí)深化篇(題目+答案)




 關(guān)于機器學(xué)習(xí)面試精講
關(guān)于機器學(xué)習(xí)面試精講










評論