有人認(rèn)為，用低精度訓(xùn)練機(jī)器學(xué)習(xí)模型會(huì)限制訓(xùn)練的精度，事實(shí)真的如此嗎？本文中，斯坦福大學(xué)的DAWN人工智能研究院介紹了一種名為bit recentering的技術(shù)，它可以用低精度的計(jì)算實(shí)現(xiàn)高準(zhǔn)確度的解決方案。以下是論智對(duì)原文的編譯，文末附原論文地址。

低精度計(jì)算在機(jī)器學(xué)習(xí)中已經(jīng)吸引了大量關(guān)注。一些公司甚至已經(jīng)開(kāi)始研發(fā)能夠原生支持并加速低精度操作的硬件了，比如微軟的腦波計(jì)劃（Project Brainwave）和谷歌的TPU。雖然使用低精度計(jì)算對(duì)系統(tǒng)來(lái)說(shuō)有很多好處，但是低精度方法仍然主要用于推理，而非訓(xùn)練。此前，低精度訓(xùn)練算法面臨著一個(gè)基本困境（fundamental tradeoff）：當(dāng)使用較少的位進(jìn)行計(jì)算時(shí)，舍棄誤差就會(huì)增加，這就限制了訓(xùn)練的準(zhǔn)確度。根據(jù)傳統(tǒng)觀點(diǎn)，這種制約限制了研究人員在系統(tǒng)中部署低精度訓(xùn)練算法的能力，但是這種限制能否改變？是否有可能設(shè)計(jì)一種使用低精度卻不會(huì)限制準(zhǔn)確度的算法呢？

答案是肯定的。在某些情況下我們可以從低精度訓(xùn)練中獲得高準(zhǔn)確度的解決方案，在這里我們使用了一種新的隨機(jī)梯度下降方法，稱為高準(zhǔn)確度低精度（HALP）法。HALP比之前的算法表現(xiàn)更好，因?yàn)樗鼫p少了兩個(gè)限制低精度隨機(jī)梯度下降準(zhǔn)確度的噪聲源：梯度方差和舍棄誤差。

為了減少梯度方差帶來(lái)的噪音，HALP使用常見(jiàn)的SVRG（stochastic variance-reduced gradient）技術(shù)。SVRG能定期使用完全梯度來(lái)減少隨機(jī)梯度下降中使用的梯度樣本的方差。

為了降低量化數(shù)字帶來(lái)的噪聲，HALP使用了名為“bit centering”的新技術(shù)，它背后的原理是，當(dāng)我們接近最優(yōu)點(diǎn)時(shí)，梯度漸變的幅度變小。也就是說(shuō)攜帶的信息變少，于是我們能對(duì)其進(jìn)行壓縮。通過(guò)動(dòng)態(tài)地重新調(diào)整低精度數(shù)字，我們可以在算法收斂時(shí)降低量化噪聲。

將這兩種技術(shù)結(jié)合，HALP能夠以和全精度SVRG同樣的線性收斂率生成任意準(zhǔn)確地解決方案，同時(shí)在低精度迭代時(shí)使用的是固定位數(shù)。這個(gè)結(jié)果顛覆了有關(guān)低精度訓(xùn)練算法的傳統(tǒng)觀點(diǎn)。

為什么低精度的隨機(jī)梯度下降有所限制？

首先先交代一下背景：我們想要解決以下這個(gè)訓(xùn)練問(wèn)題：

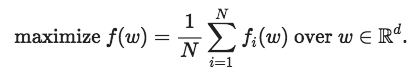
這是用來(lái)訓(xùn)練許多機(jī)器學(xué)習(xí)模型（包括深度神經(jīng)網(wǎng)絡(luò)）的經(jīng)典實(shí)證問(wèn)題：讓風(fēng)險(xiǎn)最小化。解決這個(gè)問(wèn)題的標(biāo)準(zhǔn)方法之一是隨機(jī)梯度下降，它是一種通過(guò)運(yùn)行接近最佳值的迭代算法。

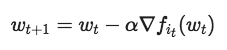
在每次迭代時(shí)，it是從{1,..., N}中隨機(jī)挑選的一個(gè)指數(shù)，我們雖然想運(yùn)行這樣的算法，但是要保證迭代wt是低精度的。也就是說(shuō)，我們希望它們使用較少位的定點(diǎn)運(yùn)算（通常為8位或16位）。但是，當(dāng)直接對(duì)隨機(jī)梯度下降更新規(guī)則而進(jìn)行這項(xiàng)操作時(shí)，我們遇到了問(wèn)題：?jiǎn)栴}的解決方案w可能無(wú)法再選中的定點(diǎn)表示中顯示出來(lái)。例如，如果一個(gè)8位的定點(diǎn)表示，可以儲(chǔ)存{-128，-127，…，127}之間的整數(shù)，正確的解決方法是w*=100.5，那么我們與解決方案的距離不可能小于0.5，因?yàn)槲覀儾荒鼙硎痉钦麛?shù)。除此之外，將梯度轉(zhuǎn)換為定點(diǎn)導(dǎo)致的舍棄誤差可能會(huì)減慢收斂速度，這也影響了低精度SGD的準(zhǔn)確性。

Bit Centering

當(dāng)我們運(yùn)行隨機(jī)梯度下降時(shí)，在某種意義上，我們世紀(jì)正對(duì)一堆梯度樣本進(jìn)行平均（或總結(jié)）。Bit Centering背后的關(guān)鍵思想是隨著梯度漸變逐漸變小，我們可以用同樣的位數(shù)、以較小的誤差對(duì)它們求平均值。想要知道為什么，想像一下，你想對(duì)[-100, 100]之間的數(shù)字求平均值，然后和[-1, 1]的平均值作比較。在前一個(gè)集合中，我們需要選擇一個(gè)定點(diǎn)表示，它可以覆蓋整個(gè)集合（例如{-128，-127，…，127}）。而在第二個(gè)集合中，我們選擇的定點(diǎn)要覆蓋[-1, 1]，例如{-128/127,-127/127,..., 126/127,127/127}。這就意味著在固定位數(shù)情況下，第二種情況中的相鄰可表示數(shù)字之間的差值比第一種情況更小，因此舍棄誤差也更低。

這個(gè)關(guān)鍵的想法讓我們得到了啟發(fā)。為了在[-1, 1]中求出比[-100, 100]中更少誤差的平均數(shù)，我們需要用一個(gè)不同的定點(diǎn)表示，即我們應(yīng)該不斷更新低精度表示：隨著梯度漸變得越小，我們應(yīng)該用位數(shù)更小的定點(diǎn)數(shù)字，覆蓋更小的范圍。

但是我們?cè)撊绾胃卤硎灸兀课覀円采w的范圍到底多大？如果目標(biāo)是帶有參數(shù)μ的強(qiáng)凸，那么不管我們何時(shí)在某一點(diǎn)w采取完整的梯度漸變是，都可以用以下公式限制最佳位置

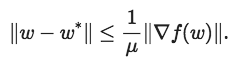
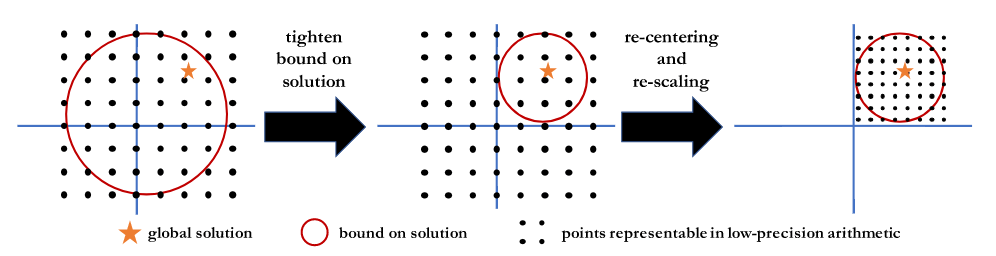
這種不等式為最終的解決方案提供了一系列可能的定位，所以無(wú)論何時(shí)計(jì)算完整梯度，我們都可以重新居中并縮放低精度表示以覆蓋此范圍。下圖說(shuō)明了這一過(guò)程。

HALP

HALP是運(yùn)行SVRG并在每個(gè)時(shí)期都使用具有完全梯度的bit centering更新低精度表示的算法。原論文有對(duì)這一方法的具體描述，在這里我們只簡(jiǎn)單做些介紹。首先，我們證明了，對(duì)于強(qiáng)凸的Lipschitz光滑函數(shù)，只要我們使用的位數(shù)b滿足

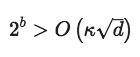
其中κ是該問(wèn)題的條件數(shù)字，那么為了適當(dāng)設(shè)置尺寸和時(shí)間長(zhǎng)度，HALP將以線性速度收斂到任意準(zhǔn)確度的解。更顯然的是，0＜γ＜1，

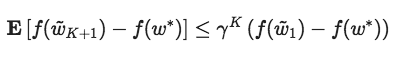
其中wk+1表示第K次迭代后的值。下表表現(xiàn)了這一變化過(guò)程

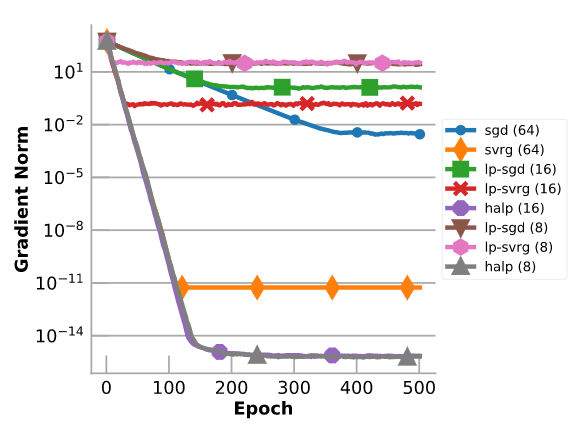
圖表通過(guò)對(duì)具有100個(gè)特征和1000個(gè)樣本的合成數(shù)據(jù)集進(jìn)行線性回歸，來(lái)評(píng)估HALP。將它與全精度梯度下降、SVRG、低精度的梯度下降和低精度的SVRG進(jìn)行比較。需要注意的是，盡管只有8位（受到浮點(diǎn)錯(cuò)誤的限制），HALP仍能收斂到精度非常高的結(jié)果上。在這種情況下，HALP可以比全精度SVRG收斂到更高精度的結(jié)果中，因?yàn)镠ALP較少使用浮點(diǎn)運(yùn)算，因此對(duì)浮點(diǎn)的非準(zhǔn)確性不敏感。