從某種程度上來說,沒有人真正理解機器學習。
這不是一個復雜的問題,我們所做的一切也都非常簡單,但由于一些天生的“障礙”,我們人類確實難以理解發生在計算機“大腦”中的那些簡單事物。
人類長久以來的生理進化決定了我們能推理二維、三維的空間,在這基礎上,我們也能靠想象思考四維空間里發生的變化。但這對于機器學習來說卻是小巫見大巫,它通常需要處理數千、數萬,甚至數百萬個維度!即便是很簡單的問題,如果我們把它放進維度非常高的空間內來解決,以人類的目前的大腦,不理解也不足為奇。
因此,直觀地感受高維空間是沒有希望的。
為了在高維空間中做一些事情,我們建立了許多工具,其中一個龐大的、發達的分支是降維,它探索的是把高維數據轉換為低維數據的技術,也為此做了大量可視化方面的工作。
所以如果我們希望可視化機器學習、深度學習,這些技術會是我們必備的基礎知識。可視化意味著我們能更直觀地感受實際正在發生的事情,我們也可以借此更深入地了解神經網絡。為了這一目的,我們要做的第一件事是理解降維,我們選擇的數據集是MNIST。
MNIST
MNIST是一個簡單的計算機視覺數據集,它由28×28像素的手寫數字圖像組成,例如:
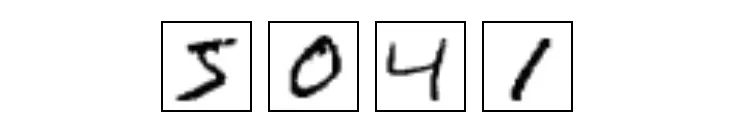
每個MNIST數據點,每個圖像,都可以被看作是描述每個像素有多暗的數字數組。例如我們可以這么看待這個手寫數字“1”:
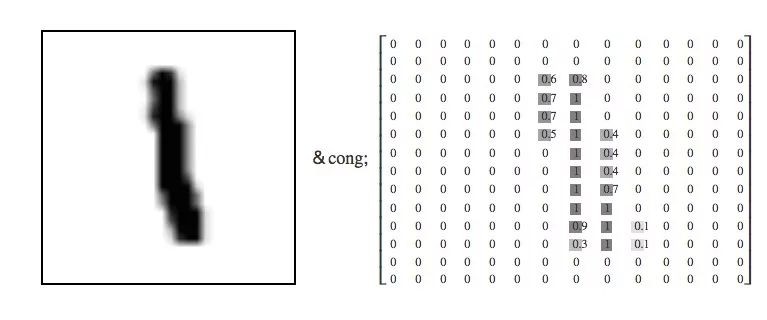
因為每個圖像的像素都是28×28,所以我們得到的其實是一個28×28的矩陣。考慮到矢量的每個分量都是介于0和1之間的一個描述明暗程度的值,如果我們把每一個值都看做是維向量,那這就是一個28×28=784的高維空間。
所以空間內的矢量其實并不都是MNIST數字,不同像素點之間的區別稱得上是天差地別。為了論證這一點,我們從圖像中隨機選取了幾個點并把它們放大——這是個像素為28×28的圖像——每個像素的顏色可能是黑色的、白色的或帶陰影灰色的。如下圖所示,選取的隨機點看起來更像是噪聲。

像MNIST數字這樣的圖像是非常罕見的,雖然數據點被嵌入在784維空間中,但它們又被包含在一個非常小的子空間內。用更復雜的話說,就是它們占據較低維的子空間。
人們對MNIST數字占據的子空間維數具體是多少有很多討論,其中流行在機器學習研究人員中的一個假設是流形理論:MNIST是一個低維流形結構,高維數據通過它嵌入高維空間中,形成掃掠和彎曲。而與拓撲數據分析更相關的另一個假設是,像MNIST數字這樣的數據具有一些觸手狀的突起,這些突起會嵌入周圍空間中。
但是事實究竟是什么,沒有人真正知道!
MNIST立方體
為了探索這一點,我們可以把MNIST數據點看作是在一個784維立方體中固定的一點。立方體的每個維度都對應一個特定的像素,根據像素強度,數據點的范圍在0到1之間。在維度的一邊,是像素為白色的圖像,在另一邊,是像素為黑色的圖像。在它們之間的是灰色圖像。
如果這樣想,一個自然而然的問題是如果我們只看到一個特定的二維面,那這個立方體看起來會是什么樣的?就像盯著一個雪球,我們只能看到投影在二維平面上的數據點,一個維度對應像素強度,另一個維度對應另一個像素。這樣做能幫助我們用原始的方式探索MNIST。
在下圖中,每個點都表示一個MNIST數據點,顏色表示所屬類別(哪個數字)。當我們把鼠標放在上面后,它的圖像會出現在各個軸上。每個軸對應特定的像素明暗強度。

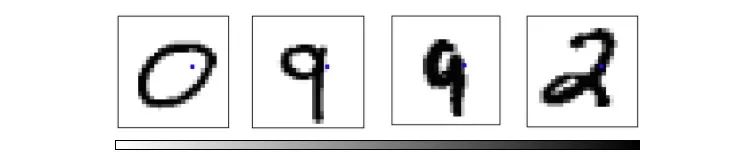
探索這個可視化有助于我們挖掘MNIST結構的一些信息。如下圖所示,如果選取坐標為p18,16和p7,12的像素,數字0會聚集在右下角,數字9則會集中在左上角。

紅色點為0,粉色點為9
如果選取坐標為p5,6和p7,9處的像素,那數字2會大量出現在右上角,數字3則集中在右下角。

黃綠色點為2,綠色點為3
這看似是個小小的進步,但我們其實不可能完全以這種方式理解MNIST。這些小發現有時并沒什么說服力,它們更像是運氣的產物,雖然我們從中窺見的關于結構的信息量很少,但這種思維方式是正確的。如果我們從平面看不到理想的數據結構,那我們也許能從某個角度來觀察這些數據。
這就牽出了第二個問題,我們該怎么選擇合適的角度。平行看數據時,我們該轉動幾度;垂直看數據時,我們又該怎么扭?好在這個難題已經有人幫我們解決了——主成分分析(PCA)。比起手動計算,PCA將會找到最多的角度(捕捉盡可能多的變化)。
從一個角度看784維的立方體意味著我們要確定立方體每個軸的傾斜方向:是向這邊、向那邊。還是兩頭向中間。具體來說,以下是PCA選出的兩個角度的圖片,紅色表示像素的尺寸向一側傾斜,藍色則表示向另一側傾斜。
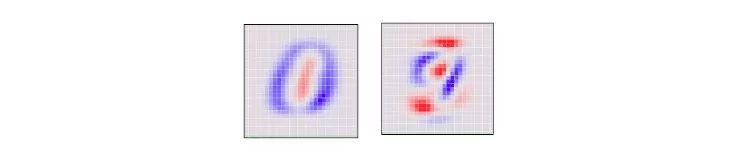
如果MNIST數字基本呈現紅色,它就在對應的一側結束,反之亦然。我們選擇PCA選擇的第一個“主要成分”作為水平角度,然后再把“大部分紅色小部分藍色”的點推向左側,把“大部分藍色小部分紅色”的點推向右側。
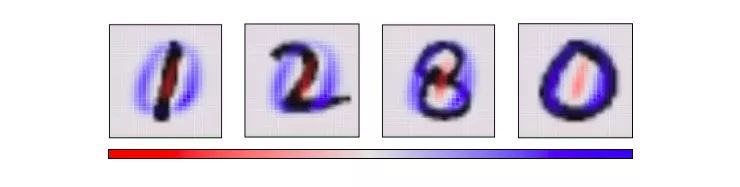
現在我們知道最佳的水平和垂直角度,我們可以嘗試從這個角度來觀察立方體。
下圖和之前的可視化動圖基本類似,不同的是它把兩個軸固定為第一個“主成分”和第二個“主成分”,也就是我們觀察數據的角度。在每個軸上的圖像中,藍色和紅色表示的是該像素的不同“傾向”。
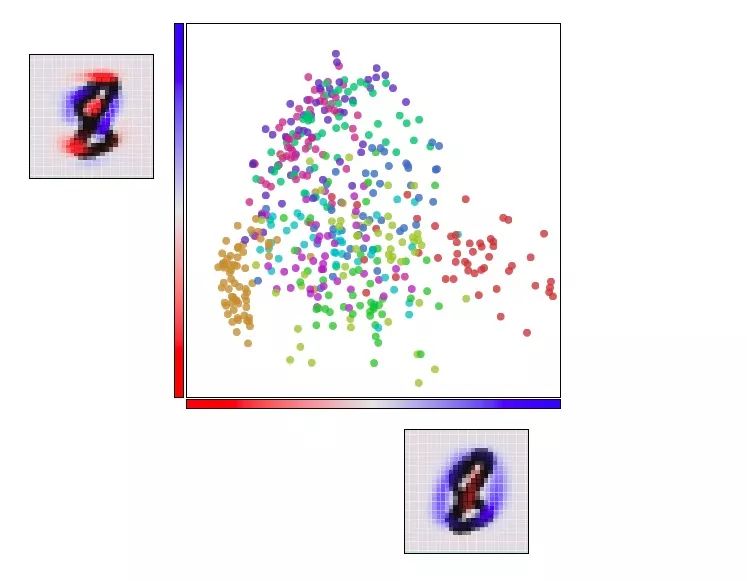
用PCA可視化MNIST
雖然效果更好了,但它還稱不上是完美的,因為即便從最好的角度觀察,MNIST的數據也不能很好地排列。這是個很特別的高維解構,簡單的線性變換還不能分解其中的復雜性。
值得慶幸的是,我們有一些強大的工具來處理這類“不友好”的數據集。
基于優化的降維
這里我們再明確一下可視化的目的——我們為什么要追求“完美”的可視化?可視化的目標又該是什么?
如果在可視化圖像中,數據點之間的距離和它們在原高維空間中的距離相同,那這就是個理想的結果。因為做到了這點,就意味著我們已經捕捉到了數據的全局分布。
更準確地說,對于MNIST圖像中的任意兩個數據點xi和xj,它們之間有兩種距離,一種是在原空間中的距離d?i,j,另一種則是在可視化圖像中的歐式距離di,j。它們之間的cost是:
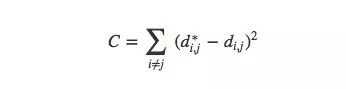
這個值是衡量可視化是好是壞的標準:只要距離不相同,那這就是個不好的可視化。如果C值過大,這意味著可視化圖像中的距離和原距離很不一樣;如果C值很小,這說明兩者十分相近;如果C值為0,我們就得到了一個“完美”的嵌入。
這聽起來就像一個優化問題了!相信任何一個深度學習研究人員都知道該怎么做——選取一個隨機點并使用梯度下降。

用MDS可視化MNIST
這種方法被稱為多維縮放(MDS)。首先,我們把每個點隨機放在一個平面上,用一個長度等于原始距離d?i,j的“彈簧”把點與點連接起來,隨著點在空間中自由移動,這個“彈簧”能依靠物理把新距離控制在可控范圍內。
當然,事實上這個cost是不會等于0的,因為在控制距離不變的情況下把高維空間嵌入二位空間是不可能的,我們也需要這種不可能。雖然還有些缺陷,但從上圖中我們可以看到,這些數據點已經顯示出了聚類趨勢,這是個進步不小的可視化。
Sammon映射
為了更盡善盡美,這里我們再引入MDS的一個變體——Sammon映射。首先要聲明一點,就是MDS有很多變體,而且它們的共同特征是認為cost函數強調數據的局部結構比整體結構更重要。當采用中心化的內積計算鄰近矩陣時,我們希望原始距離和主成分是相等的,為了捕捉更多可能性,Sammon映射的做法是保護較小的距離。
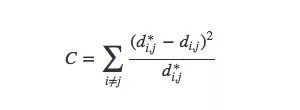
如下圖所示,比起關注距離較遠兩點的位置,Sammon映射更關注附近點的距離控制,如果說某兩個點原距離是其他兩點的二分之一,那它們被“重視”的程度會是后者的兩倍。
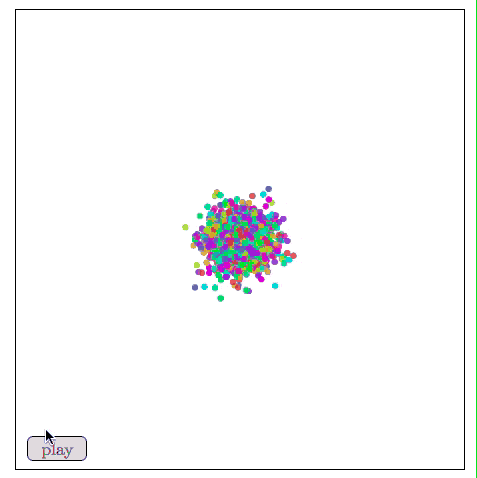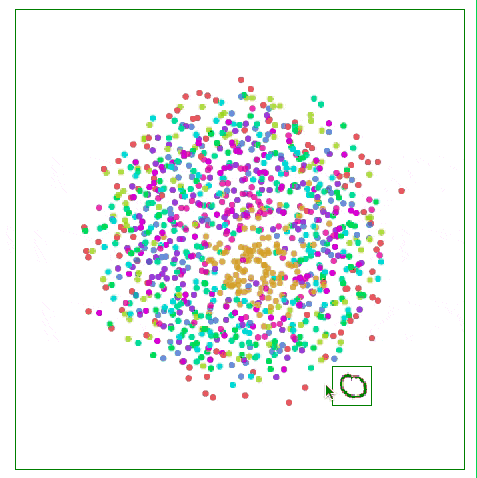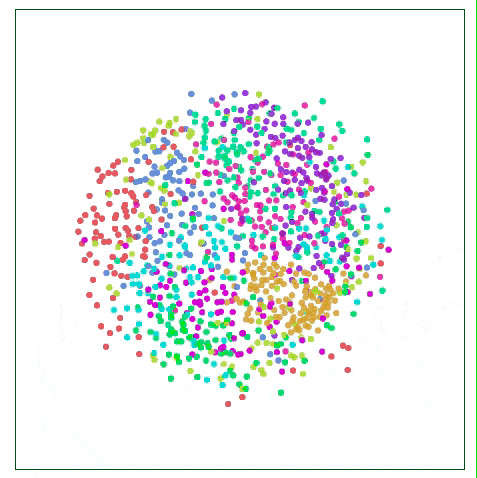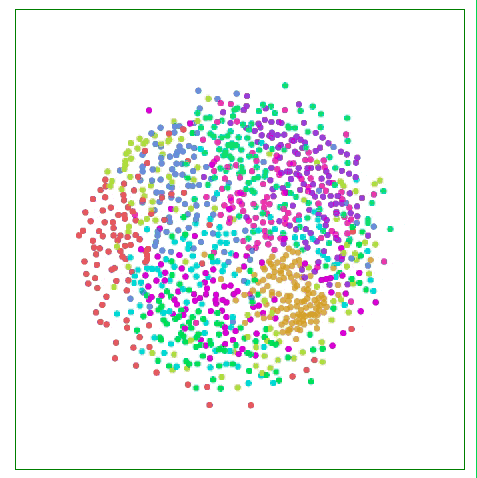
用Sammon映射可視化MNIST
對于MNIST,這種方法并沒有顯示出太大的不同,這是因為高維空間中數據點的距離不夠直觀,例如MNIST中的相同數字“1”之間的距離:
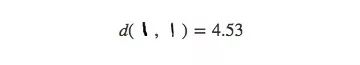
或者不同的數字“9”和“3”之間的距離(比前者的3倍要少一些):
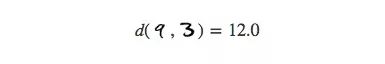
對于相同的數字,它們身上的不同細節變化數不勝數,因此它們的實際平均距離會比我們想象中的高不少。相反地,對于本身距離很遠的數字,它們的差異隨距離增加,因此遇到兩個完全不同的數字也在情理之中。簡而言之,在高維空間中,相同數字之間的距離和不同數字之間距離的差距并沒有我們想象中的那么大。
基于圖像的可視化
因此,如果我們最終希望得到的是低維空間嵌入結果,那優化的目標應該更明確。
我們可以假設存在一個和MNIST距離最接近的圖(V,E),它之中的節點就是MNIST里的數據點,并且這些點都連接到原始空間中最接近它的三個點。有了它,我們就能丟掉高維信息,只需思考它嵌入地位空間的方式。
給定這樣的圖,我們可以使用標準圖形布局算法來可視化MNIST。 force-directed graph drawing是一種繪圖方法,它的做法是將圖的節點定位在二維或三維空間中,使得所有的邊或多或少具有相等的長度。在這里,我們可以假設所有數據點都是互相排斥的帶電粒子,距離是“彈簧”,這樣做之后得到的cost函數就是:
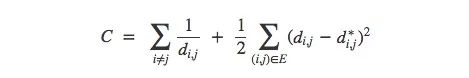

用圖像可視化MNIST
上圖發現了MNIST中的很多結構,尤其是它似乎找到了不同的MNIST類。雖然它們重疊,但在圖像布局優化期間,我們可以發現聚類之間的相互滑動。由于這些連接,最終嵌入低維平面時它們還是保持重疊狀態,但我們起碼看到了cost函數試圖分離它們的嘗試。
這也是基于圖像的可視化的一個優點。在之前的可視化嘗試中,即便我們在某個聚類里看到了某個點,我們也無法確定它是否真的在那兒。但圖像可以完全規避這一點,例如如果我們檢查著色為紅色的數字“0”數據點聚類,我們可以在里面發現一個藍色點“6”,查看它周圍的數據點我們就能知道,這個“6”之所以被歸類在這里是因為它寫的太差了,長得更像個“0”。
t-SNE
t-SNE是本文介紹的最后一種降維方法,它在深度學習中非常受歡迎,但考慮到其中涉及不少數學知識,所以我們得先理一理。
粗略地說,t-SNE試圖優化的東西是保存數據的拓撲結構。對于每一點,它構造了一個概念,即周圍的其他點都是它的“鄰居”,我們要試圖使所有點具有相同數量的“鄰居”。因此它的目標就是嵌入并使各個點擁有的“鄰居”數相同。
在某些方面,t-SNE很像基于圖像的可視化,但它的特色在于將數據點之間的關聯性轉換為概率,這個點可能是“鄰居”,也可能不是“鄰居”,每個點成為“鄰居”的程度不同。
用t-SNE可視化MNIST
t-SNE通常在揭示數據集聚類和子聚類中有優秀表現,但它容易陷入局部最小值。如下圖所示,兩側的紅點“0”因為中間的藍點“6”無法聚集在一起。
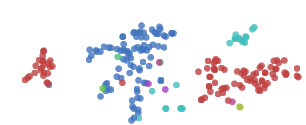
一些技巧可以幫助我們避免這些糟糕的局部極小值。其中首選的方法是增大數據量,考慮到這是一篇演示文章,我們在這里只用了1000個樣本,如果用上MNIST全部50000多個數據點,效果會更好。另外就是用模擬退火、調超參等。下圖是一個比較好的可視化:
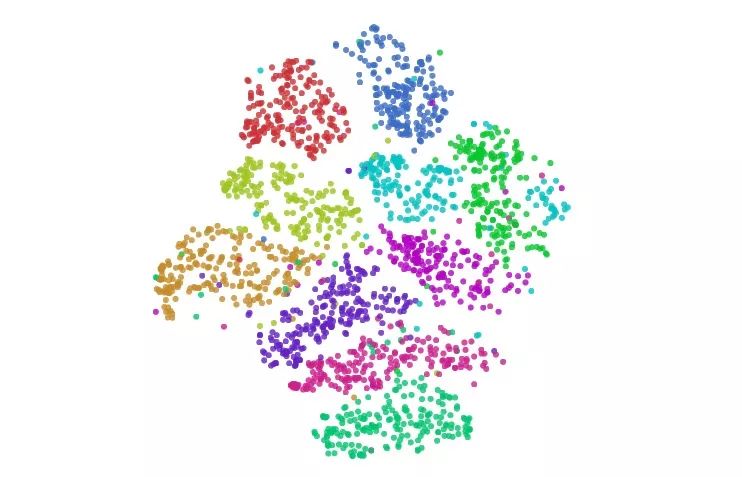
用t-SNE可視化MNIST
在Maaten & Hinton(2008)最初那篇介紹t-SNE的論文里,他們給出了一些更完美的可視化結果,感興趣的讀者可以前往一讀。
在我們上面的例子中,t-SNE不僅給出了最好的聚類,我們也可以通過圖像從中推測一些東西。

用t-SNE可視化MNIST
圖中數字“1”這個聚類被橫向水平拉伸,從左向右查看數據點,我們觀察到了這個趨勢:
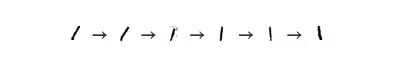
這些“1”先向左傾,再直立,最后向右傾。對此一個靠譜的想法是在MNIST中,相同數字變化的主要因素是傾斜。這很可能是因為MNIST通過多種方式使數字標準化,而這些變化又以直立的手寫體為分界線分屬兩邊。這種情況不是孤例,其他數字的分布也或多或少表現出了這個特點。
三維可視化
除了降維到二維平面,三維也是非常常見的一個維度。考慮到之前在平面中許多聚類有重疊,因此我們也可視化了MNIST數字降維到三維的一些情況。

用圖像可視化MNIST(3D版)
不出所料,三維版本效果更好。這些聚類分離地很徹底,并且在糾纏時不再重疊。
看到這里我們就能知道為什么分類MNIST數字的準確率達到95%左右很容易,但越往上就越難。在可視化圖像中,這些數據的分類十分清晰,因此但凡性能較好的分類器都能達成任務目標。如果要更細化,這就很難了,因為有些手寫體確實難以歸類。

用MDS可視化MNIST(3D版)
看來MDS的二維比三維表現更好一點。

用t-SNE可視化MNIST
因為t-SNE假想了一大堆鄰居,所以各聚類分得更散。但總體而言,它的效果還是不錯。
如果你想要將高維數據可視化,那么在三維空間應該比二維更適合。
小結
降維是一個非常發達的領域,本文只抓住了事物表面,還有上百種方法亟待測試,所以各位讀者可以親自動手去試一試。
人們往往很容易陷入一種思維,固執地認定其中一種技術比其他技術更好。但我認為其實大部分方法都是互補的,它們為了做到權衡,都必須放棄一個點來抓住另一個點,如PCA嘗試保留線性結構,MDS嘗試保留全局幾何,而t-SNE嘗試保留拓撲(鄰域結構)。
這些技術為我們提供了一種獲得理解高維數據的方法。盡管直接試圖用人的思想來理解高維數據幾乎是無望的,但通過這些工具,我們可以開始取得進展。
-
圖像
+關注
關注
2文章
1088瀏覽量
40526 -
機器學習
+關注
關注
66文章
8435瀏覽量
132885 -
數據集
+關注
關注
4文章
1209瀏覽量
24772
原文標題:可視化MNIST:探索圖像降維過程
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 MNIST是一個簡單的計算機視覺數據集
MNIST是一個簡單的計算機視覺數據集











評論