本文將介紹信息量,熵,交叉熵,相對熵的定義,以及它們與機器學習算法中代價函數的定義的聯系。
1. 信息量
信息的量化計算: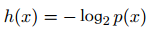
解釋如下:
信息量的大小應該可以衡量事件發生的“驚訝程度”或不確定性:
如果有人告訴我們一個相當不可能的事件發生了,我們收到的信息要多于我們被告知某個很可能發?的事件發?時收到的信息。如果我們知道某件事情?定會發?,那么我們就不會接收到信息。 也就是說,信息量應該連續依賴于事件發生的概率分布p(x)。因此,我們想要尋找一個基于概率p(x)計算信息量的函數h(x),它應該具有如下性質:
h(x) >= 0,因為信息量表示得到多少信息,不應該為負數。
h(x, y) = h(x) + h(y),也就是說,對于兩個不相關事件x和y,我們觀察到兩個事件x, y同時發?時獲得的信息應該等于觀察到事件各?發?時獲得的信息之和;
h(x)是關于p(x)的單調遞減函數,也就是說,事件x越容易發生(概率p(x)越大),信息量h(x)越小。
又因為如果兩個不相關事件是統計獨?的,則有p(x, y) =p(x)p(y)。根據不相關事件概率可乘、信息量可加,很容易想到對數函數,看出h(x)一定與p(x)的對數有關。因此,有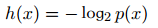 滿足上述性質。
滿足上述性質。
2. 熵(信息熵)
對于一個隨機變量X而言,它的所有可能取值的信息量的期望就稱為熵。熵的本質的另一種解釋:最短平均編碼長度(對于離散變量)。
離散變量:
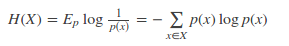
連續變量:
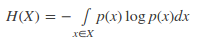
3. 交叉熵
現有關于樣本集的2個概率分布p和q,其中p為真實分布,q非真實分布。按照真實分布p來衡量識別一個樣本的熵,即基于分布p給樣本進行編碼的最短平均編碼長度為:
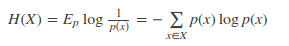
如果使用非真實分布q來給樣本進行編碼,則是基于分布q的信息量的期望(最短平均編碼長度),由于用q來編碼的樣本來自分布p,所以期望與真實分布一致。所以基于分布q的最短平均編碼長度為:
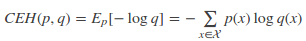
上式CEH(p, q)即為交叉熵的定義。
4. 相對熵
將由q得到的平均編碼長度比由p得到的平均編碼長度多出的bit數,即使用非真實分布q計算出的樣本的熵(交叉熵),與使用真實分布p計算出的樣本的熵的差值,稱為相對熵,又稱KL散度。
KL(p, q) = CEH(p, q) - H(p)=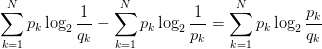
相對熵(KL散度)用于衡量兩個概率分布p和q的差異。注意,KL(p, q)意味著將分布p作為真實分布,q作為非真實分布,因此KL(p, q) != KL(q, p)。
5. 機器學習中的代價函數與交叉熵
若 p(x)是數據的真實概率分布, q(x)是由數據計算得到的概率分布。機器學習的目的就是希望q(x)盡可能地逼近甚至等于p(x) ,從而使得相對熵接近最小值0. 由于真實的概率分布是固定的,相對熵公式的后半部分(-H(p))就成了一個常數。那么相對熵達到最小值的時候,也意味著交叉熵達到了最小值。對q(x)的優化就等效于求交叉熵的最小值。另外,對交叉熵求最小值,也等效于求最大似然估計(maximum likelihood estimation)。
特別的,在logistic regression中,p:真實樣本分布,服從參數為p的0-1分布,即X~B(1,p)
p(x = 1) = y
p(x = 0) = 1 - yq:待估計的模型,服從參數為q的0-1分布,即X~B(1,q)
p(x = 1) = h(x)
p(x = 0) = 1-h(x)
其中h(x)為logistic regression的假設函數。兩者的交叉熵為:
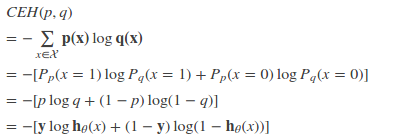
對所有訓練樣本取均值得:
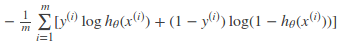
這個結果與通過最大似然估計方法求出來的結果一致。使用最大似然估計方法參加博客Logistic Regression.
-
函數
+關注
關注
3文章
4338瀏覽量
62739 -
機器學習
+關注
關注
66文章
8424瀏覽量
132765 -
交叉熵
+關注
關注
0文章
4瀏覽量
2379
原文標題:信息量,熵,交叉熵,相對熵與代價函數
文章出處:【微信號:AI_shequ,微信公眾號:人工智能愛好者社區】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于交叉熵算法的跟馳模型標定

當機器學習遇上SSD,會擦出怎樣的火花呢?
機器學習和深度學習中分類與回歸常用的幾種損失函數




 機器學習中的代價函數與交叉熵
機器學習中的代價函數與交叉熵
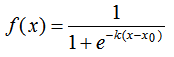
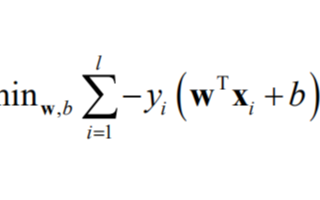










評論