機器學習初創公司Mate Labs聯合創始人Kailash Ahirwar簡要介紹了13種神經網絡激活函數。

激活函數將非線性引入網絡，因此激活函數自身也被稱為非線性。神經網絡是普適的函數逼近器，而深度神經網絡基于反向傳播訓練，因此要求可微激活函數。反向傳播在這一函數上應用梯度下降，以更新網絡的權重。理解激活函數非常重要，因為它對深度神經網絡的質量起著關鍵的作用。本文將羅列和描述不同的激活函數。

線性激活函數

恒等函數（Identity）或線性激活（Linear activation）函數是最簡單的激活函數。輸出和輸入成比例。線性激活函數的問題在于，它的導數是常數，梯度也是常數，梯度下降無法工作。

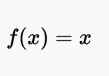
值域：(-∞, +∞)

例子：f(2) = 2或f(-4) = -4

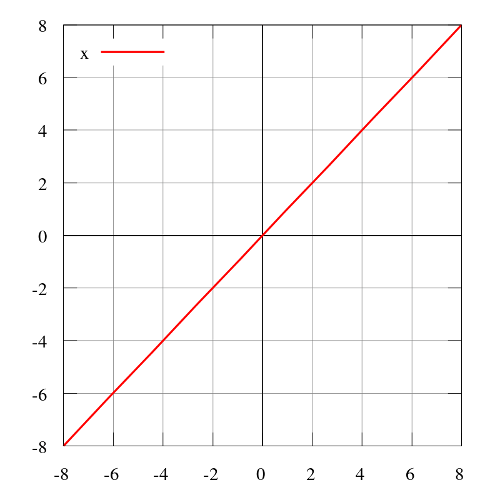
階躍函數

階躍函數（Heaviside step function）通常只在單層感知器上有用，單層感知器是神經網絡的早期形式，可用于分類線性可分的數據。這些函數可用于二元分類任務。其輸出為A1（若輸入之和高于特定閾值）或A0（若輸入之和低于特定閾值）。感知器使用的值為A1 = 1、A0 = 0.

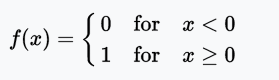
值域：0或1

例子：f(2) = 1、f(-4) = 0、f(0) = 0、f(1) = 1

圖片來源：維基百科

sigmoid函數

sigmoid函數，也稱邏輯激活函數（Logistic activation function）最常用于二元分類問題。它有梯度消失問題。在一定epoch數目之后，網絡拒絕學習，或非常緩慢地學習，因為輸入（X）導致輸出（Y）中非常小的改動。現在，sigmoid函數主要用于分類問題。這一函數更容易碰到后續層的飽和問題，導致訓練變得困難。計算sigmoid函數的導數非常簡單。

就神經網絡的反向傳播過程而言，每層（至少）擠入四分之一的誤差。因此，網絡越深，越多關于數據的知識將“丟失”。某些輸出層的“較大”誤差可能不會影響相對較淺的層中的神經元的突觸權重（“較淺”意味著接近輸入層）。

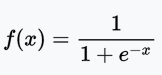
sigmoid函數定義

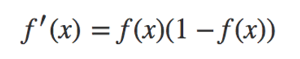
sigmoid函數的導數

值域：(0, 1)

例子：f(4) = 0.982、f(-3) = 0.0474、f(-5) = 0.0067

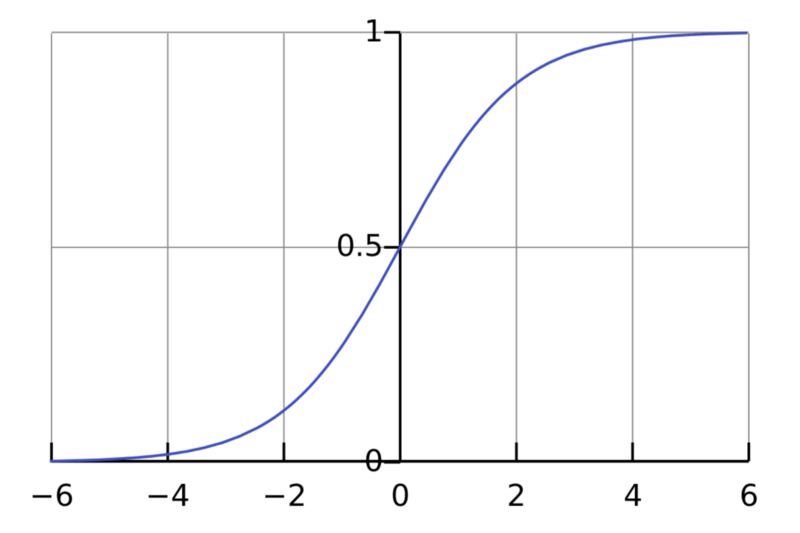
圖片來源：維基百科

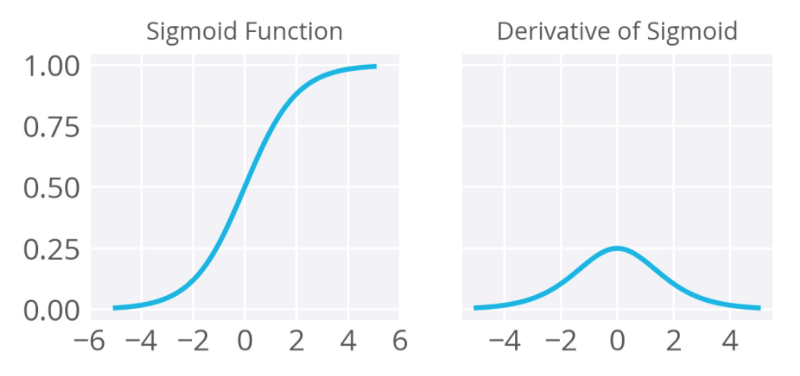
圖片來源：deep learning nano foundation

tanh函數

tanh函數是拉伸過的sigmoid函數，以零為中心，因此導數更陡峭。tanh比sigmoid激活函數收斂得更快。

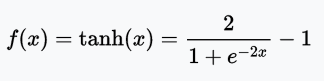
值域：(-1, 1)

例子：tanh(2) = 0.9640、tanh(-0.567) = -0.5131、tanh(0) = 0

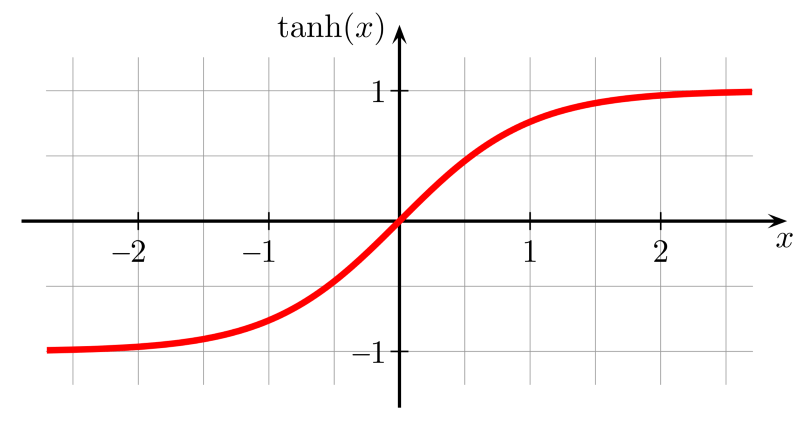
圖片來源：維基百科

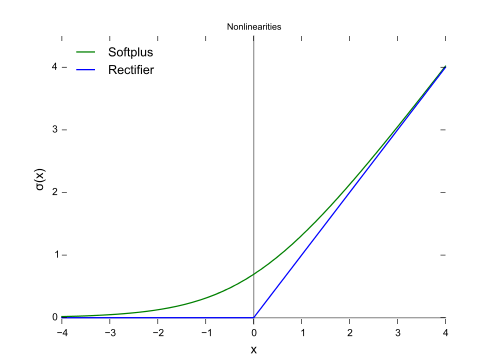
ReLU函數

ReLU（Rectified Linear Unit，修正線性單元）訓練速度比tanh快6倍。當輸入值小于零時，輸出值為零。當輸入值大于等于零時，輸出值等于輸入值。當輸入值為正數時，導數為1，因此不會出現sigmoid函數反向傳播時的擠壓效應。

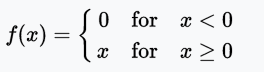
值域：[0, x)

例子：f(-5) = 0、f(0) = 0、f(5) = 5

圖片來源：維基百科

不幸的是，ReLU在訓練時可能很脆弱，可能“死亡”。例如，通過ReLU神經元的較大梯度可能導致權重更新過頭，導致神經元再也不會因為任何數據點激活。如果這一情況發生了，經過這一單元的梯度從此以后將永遠為零。也就是說，ReLU單元可能在訓練中不可逆地死亡，因為它們被從數據流形上踢出去了。例如，你可能發現，如果學習率設置過高，40%的網絡可能“死亡”（即神經元在整個訓練數據集上永遠不會激活）。設置一個合適的學習率可以緩解這一問題。

-- Andrej Karpathy CS231n 課程

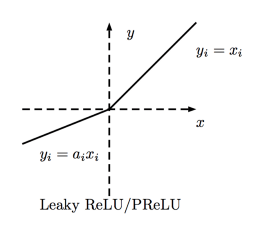
Leaky ReLU函數

Leaky ReLU讓單元未激活時能有一個很小的非零梯度。這里，很小的非零梯度是0.01.

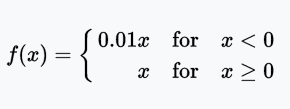
值域：(-∞, +∞)

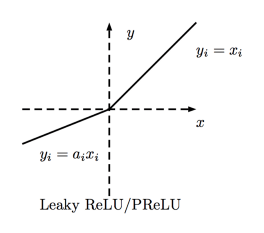
PReLU函數

PReLU（Parametric Rectified Linear Unit）函數類似Leaky ReLU，只不過將系數（很小的非零梯度）作為激活函數的參數，該參數和網絡的其他參數一樣，在訓練過程中學習。

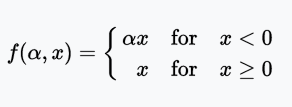
值域：(-∞, +∞)

RReLU函數

RReLU也類似Leaky ReLU，只不過系數（較小的非零梯度）在訓練中取一定范圍內的隨機值，在測試時固定。

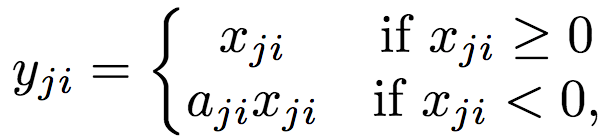
值域：(-∞, +∞)

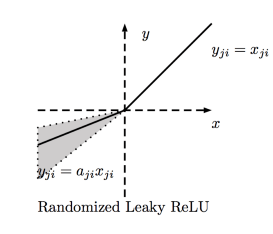
ELU函數

ELU（Exponential Linear Unit，指數線性單元）嘗試加快學習速度。基于ELU，有可能得到比ReLU更高的分類精確度。這里α是一個超參數（限制：α ≥ 0）。

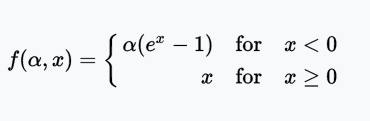
值域：(-α, +∞)

SELU函數

SELU（Scaled Exponential Linear Unit，拉伸指數線性單元）是ELU經過拉伸的版本。

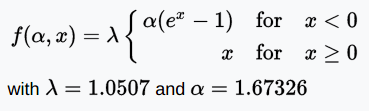
圖片來源：Elior Cohen

SReLU函數

SReLU（S-shaped Rectified Linear Activation Unit，S型修正線性激活單元）由三個分段線性函數組成。系數作為參數，將在網絡訓練中學習。

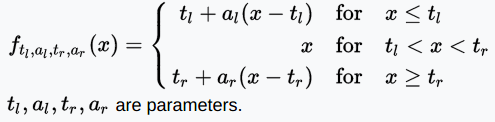
值域：(-∞, +∞)

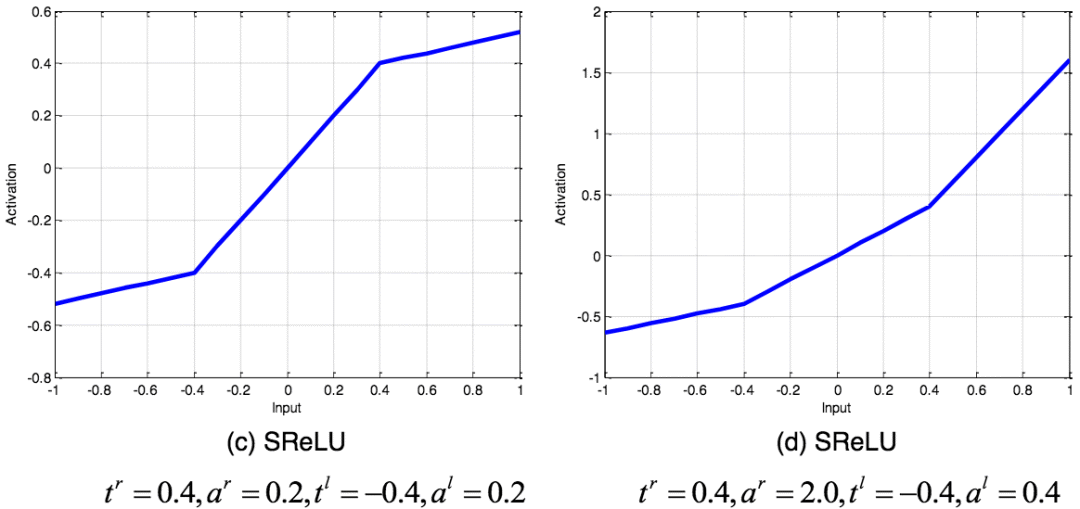
不同參數的SReLU圖像；圖片來源：arXiv:1512.07030

APL函數

APL（Adaptive Piecewise Linear，自適應分段線性）函數

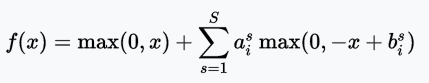
圖片來源：arXiv:1512.07030

值域：(-∞, +∞)

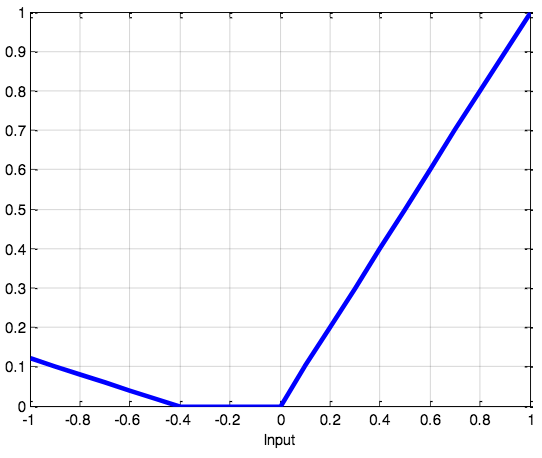
SoftPlus函數

SoftPlus函數的導數為邏輯（logistic）函數。大體上，ReLU和SoftPlus很相似，只不過SoftPlus在接近零處平滑可微。另外，計算ReLU及其導數要比SoftPlus容易很多。

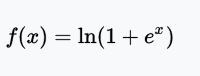
值域：(0, ∞)

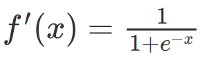
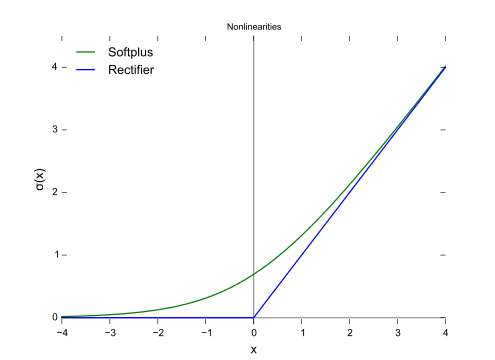
圖片來源：維基百科

bent identity函數

bent identity函數，顧名思義，將恒等函數彎曲一下。

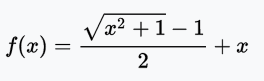
值域：(-∞, +∞)

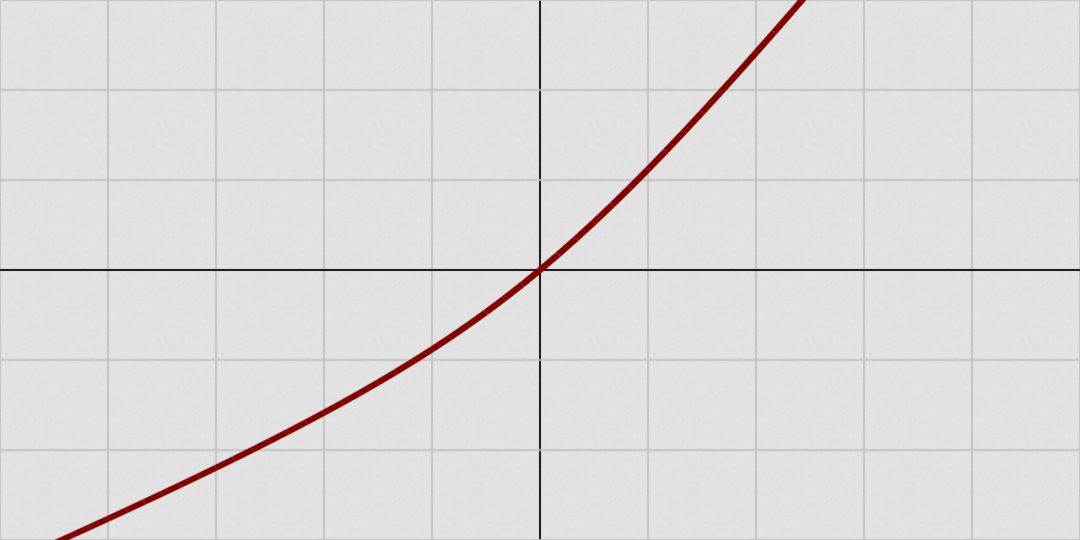
圖片來源：維基百科

softmax函數

softmax函數將原始值轉換為后驗分布，可用于衡量確定性。類似sigmoid，softmax將每個單元的輸出值擠壓到0和1之間。不過，softmax同時確保輸出的總和等于1.

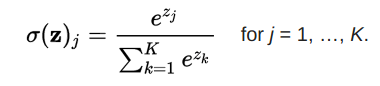
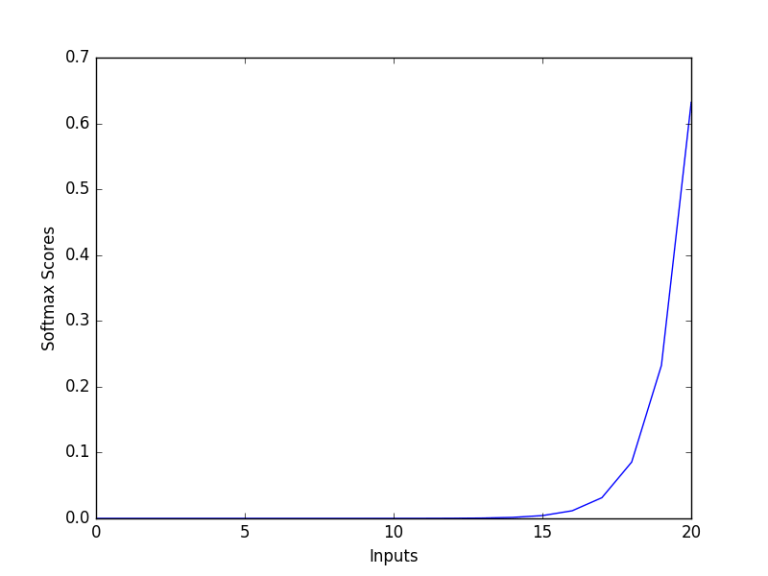
圖片來源：dataaspirant.com

softmax函數的輸出等價于類別概率分布，它告訴你任何分類為真的概率。

結語

選擇激活函數時，優先選擇ReLU及其變體，而不是sigmoid或tanh。同時ReLU及其變體訓練起來更快。如果ReLU導致神經元死亡，使用Leaky ReLU或者ReLU的其他變體。sigmoid和tanh受到消失梯度問題的困擾，不應該在隱藏層中使用。隱藏層使用ReLU及其變體較好。使用容易求導和訓練的激活函數。