1 簡介

SVD 全稱：Singular Value Decomposition。SVD 是一種提取信息的強大工具，它提供了一種非常便捷的矩陣分解方式，能夠發現數據中十分有意思的潛在模式。

主要應用領域包括：

隱性語義分析 (Latent Semantic Analysis, LSA) 或隱性語義索引 (Latent Semantic Indexing, LSI)；

推薦系統 (Recommender system)，可以說是最有價值的應用點；

矩陣形式數據（主要是圖像數據）的壓縮。

2 線性變換

在做 SVD 推導之前，先了解一下線性變換，以 2*2 的線性變換矩陣為例，先看簡單的對角矩陣：

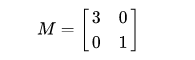
從集合上講， M 是將二維平面上的點（x，y） 經過線性變換到另一個點的變換矩陣，如下所示：

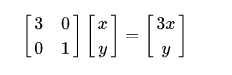
該變換的幾何效果是，變換后的平面沿著x水平方向進行了3倍拉伸，垂直方向沒有發生變化。

3 SVD 推導

該部分的推導從幾何層面上去理解二維的SVD，總體的思想是：借助 SVD 可以將一個相互垂直的網格 (orthogonal grid) 變換到另外一個互相垂直的網格。

可以通過二維空間中的向量來描述這件事情。

首先，選擇兩個互相正交的單位向量v1和v2（也可稱為一組正交基）。

M 是一個變換矩陣。

向量Mv1 , Mv2也是一組正交向量（也就是v1和v2經過M變換得到的）。

u1， u2分別是Mv1, Mv2的單位向量（即另一組正交基），且有：

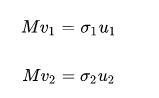
則，σ1，σ2分別為Mv1 , Mv2的模（也稱為M的奇異值）。

設任意向量x，有：

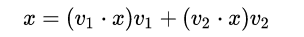
根據線代知識，向量的內積可用向量的轉置來表示：

至此，SVD 使用幾何意義的形式推導完畢，其中：

關于 SVD 的一些重要的結論性總結：

任意的矩陣M是可以分解成三個矩陣；

V表示了原始域的標準正交基；

U表示經過M變換后的新標準正交基；

∑表示了V中的向量與U中相對應向量之間的比例（伸縮）關系；

∑中的每個σ會按從大到小排好順序，值越大代表該維度重要性越高；

在利用 SVD 做數據信息提取或壓縮時，往往依據一些啟發式策略，如直接設定只提取∑ 中的前k項，或者另一種較常用的做法是保留矩陣中一定百分比的能量信息，一般可設定為 90%，能量信息比例的計算可先求得所有奇異值平方總和，然后將奇異值的平方依次累加到總值的 90% 為止，形如：

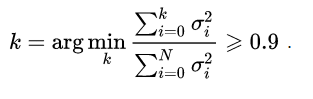
# -*- coding: utf-8 -*-

import numpy as np

import numpy.linalg as la

import matplotlib.pyplot as plt

from sklearn import datasets

from skimage import io

def getImgAsMat(index):

ds = datasets.fetch_olivetti_faces()

return np.mat(ds.images[index])

def getImgAsMatFromFile(filename):

img = io.imread(filename, as_grey=True)

return np.mat(img)

def plotImg(imgMat):

plt.imshow(imgMat, cmap=plt.cm.gray)

plt.show()

def recoverBySVD(imgMat, k):

# singular value decomposition

U, s, V = la.svd(imgMat)

# choose top k important singular values (or eigens)

Uk = U[:, 0:k]

Sk = np.diag(s[0:k])

Vk = V[0:k, :]

# recover the image

imgMat_new = Uk * Sk * Vk

return imgMat_new

# -------------------- main --------------------- #

#A = getImgAsMat(0)

#plotImg(A)

#A_new = recoverBySVD(A, 20)

#plotImg(A_new)

A = getImgAsMatFromFile('D:/pic.jpg')

plotImg(A)

A_new = recoverBySVD(A, 30)

plotImg(A_new)