如何賦予機器自主學習的能力，一直是人工智能領域的研究熱點。

強化學習與寬度學習

如何賦予機器自主學習的能力，一直是人工智能領域的研究熱點。在越來越多的復雜現實場景任務中，需要利用深度學習、寬度學習來自動學習大規模輸入數據的抽象表征，并以此表征為依據進行自我激勵的強化學習，優化解決問題的策略。深度與寬度強化學習技術在游戲、機器人控制、參數優化、機器視覺等領域中的成功應用，使其被認為是邁向通用人工智能的重要途徑。

澳門大學講座教授，中國自動化學會副理事長陳俊龍在中國自動化學會第5期智能自動化學科前沿講習班作了題目為「從深度強化學習到寬度強化學習：結構，算法，機遇及挑戰」的報告。

陳俊龍教授的報告大致可以分為三個部分。首先討論了強化學習的結構及理論，包括馬爾科夫決策過程、強化學習的數學表達式、策略的構建、估計及預測未來的回報。然后討論了如何用深度神經網絡學習來穩定學習過程及特征提取、如何利用寬度學習結構跟強化學習結合。最后討論了深度、寬度強化學習帶來的機遇與挑戰。

強化學習結構與理論

陳教授用下圖簡單描述強化學習過程。他介紹道所謂強化學習就是智能體在完成某項任務時，通過動作A與環境（environment）進行交互，在動作A和環境的作用下，智能體會產生新的狀態，同時環境會給出一個立即回報。如此循環下去，經過數次迭代學習后，智能體能最終地學到完成相應任務的最優動作。

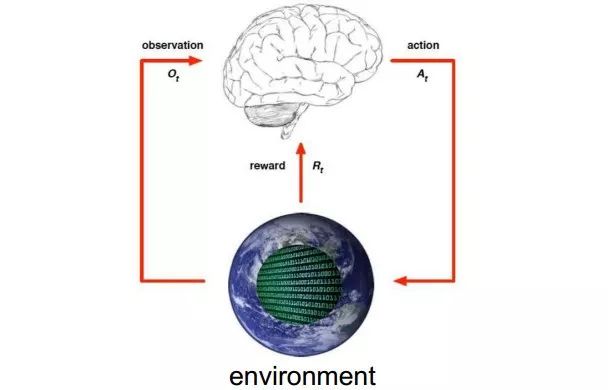
提到強化學習就不得不提一下Q-Learning。接著他又用了一個例子來介紹了強化學習Q-Learning的原理。

Q-learning

假設一個樓層共有5個房間，房間之間通過一道門連接，如下圖所示。房間編號為0~4，樓層外的可以看作是一個大房間，編號5。

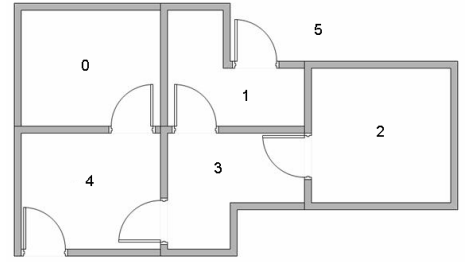
可以用圖來表示上述的房間，將每一個房間看作是一個節點，每道門看作是一條邊。

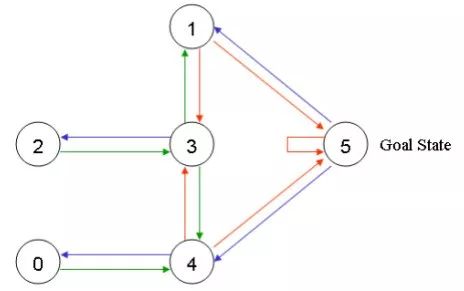
在任意一個房間里面放置一個智能體，并希望它能走出這棟樓，也可以理解為進入房間5。可以把進入房間5作為最后的目標，并為可以直接到達目標房間的門賦予100的獎勵值，那些未與目標房間相連的門則賦予獎勵值0。于是可以得到如下的圖。

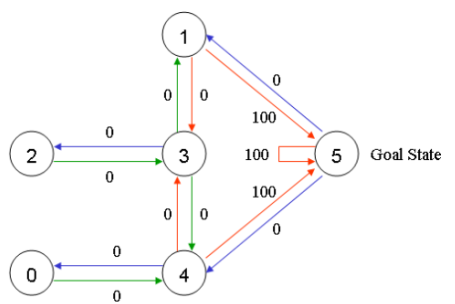
根據上圖可以得到獎勵表如下，其中-1代表著空值，表示節點之間無邊相連。

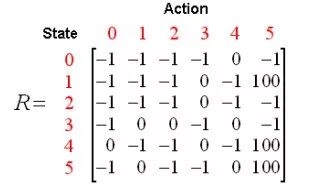
再添加一個類似的Q矩陣，代表智能體從經驗中所學到的知識。矩陣的行代表智能體當前的狀態，列代表到達下一狀態的可能動作。

然后陳教授又介紹了Q-Learning的轉換規則，即Q(state, action)=R(state, action) + Gamma * Max(Q[next state, all actions])。

依據這個公式，矩陣Q中的一個元素值就等于矩陣R中相應元素的值與學習變量Gamma乘以到達下一個狀態的所有可能動作的最大獎勵值的總和。

為了具體理解Q-Learning是怎樣工作的，陳教授還舉了少量的例子。

首先設置Gamma為0.8，初始狀態是房間1。

對狀態1來說，存在兩個可能的動作：到達狀態3，或者到達狀態5。通過隨機選擇，選擇到達狀態5。智能體到達了狀態5，將會發生什么？觀察R矩陣的第六行，有3個可能的動作，到達狀態1,4或者5。根據公式Q(1, 5) = R(1, 5) + 0.8 * Max[Q(5, 1), Q(5, 4), Q(5, 5)] = 100 + 0.8 * 0 = 100，由于矩陣Q此時依然被初始化為0，Q(5, 1), Q(5, 4), Q(5, 5) 全部是0，因此，Q(1, 5) 的結果是100，因為即時獎勵R(1,5) 等于100。下一個狀態5現在變成了當前狀態，因為狀態5是目標狀態，故算作完成了一次嘗試。智能體的大腦中現在包含了一個更新后的Q矩陣。

對于下一次訓練，隨機選擇狀態3作為初始狀態。觀察R矩陣的第4行，有3個可能的動作，到達狀態1,2和4。隨機選擇到達狀態1作為當前狀態的動作。現在，觀察矩陣R的第2行，具有2個可能的動作：到達狀態3或者狀態5。現在計算Q 值：Q(3, 1) = R(3, 1) + 0.8 * Max[Q(1, 2), Q(1, 5)] = 0 + 0.8 *Max(0, 100) = 80，使用上一次嘗試中更新的矩陣Q得到：Q(1, 3) = 0 以及 Q(1, 5) = 100。因此，計算的結果是Q(3,1)=80。現在，矩陣Q如下。

智能體通過多次經歷學到更多的知識之后，Q矩陣中的值會達到收斂狀態。如下。

通過對Q中的所有的非零值縮小一定的百分比，可以對其進行標準化，結果如下。

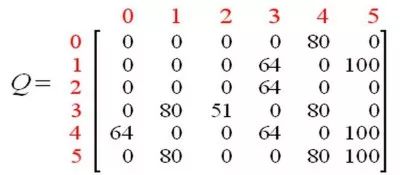
一旦矩陣Q接近收斂狀態，我們就知道智能體已經學習到了到達目標狀態的最佳路徑。

至此陳教授已經把Q-learning簡單介紹完了。通過上文的介紹大致可以總結出強化學習的六個特點：

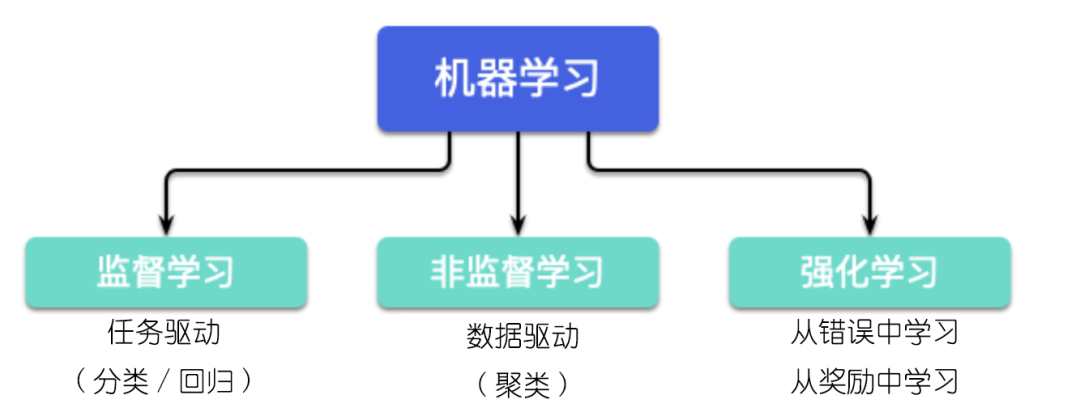
無監督，只有獎勵信號

不需要指導學習者

不停的試錯

獎勵可能延遲（犧牲短期收益換取更大的長期收益）

需要探索和開拓

目標導向的智能體與不確定的環境間的交互是個全局性的問題

四個要素：

一、策略：做什么？

1）確定策略：a=π（s）

2）隨機策略：π（a|s）=p[at=a|st=s]，st∈S，at∈A（St），∑π（a|s）=1

二、獎勵函數：r（在狀態轉移的同時，環境會反饋給智能體一個獎勵）

三、累積獎勵函數：V（一個策略的優劣取決于長期執行這一策略后的累積獎勵），常見的長期累積獎勵如下：

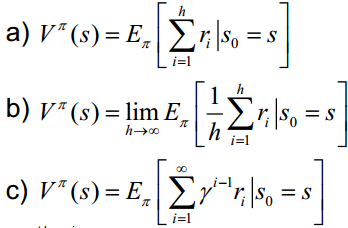
四、模型：用于表示智能體所處環境，是一個抽象概念，對于行動決策十分有用。

所有的強化學習任務都是馬爾科夫決策過程，陳教授對MDP的介紹如下。

一個馬爾可夫決策過程由一個五元組構成M =（S，A，p，γ，r）。其中S是狀態集，A是動作集，p是狀態轉移概率，γ是折扣因子，r是獎勵函數。

陳教授在介紹強化學習這部分的最后提到了目前強化學習面臨的兩大挑戰。

信度分配：之前的動作會影響當前的獎勵以及全局獎勵

探索開拓：使用已有策略還是開發新策略

Q-Learning可以解決信度分配的問題。第二個問題則可以使用ε-greedy算法，SoftMax算法，Bayes bandit算法，UCB算法來處理等。

值函數（對未來獎勵的一個預測）可分為狀態值函數和行為值函數。

1. 狀態值函數Vπ（s）：從狀態s出發，按照策略π采取行為得到的期望回報，

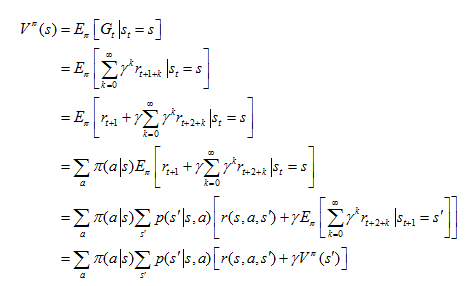
也被稱為Bellman方程。

2. 行為價值函數Qπ（s，a）：從狀態s出發采取行為a后，然后按照策略π采取行動得到的期望回報，

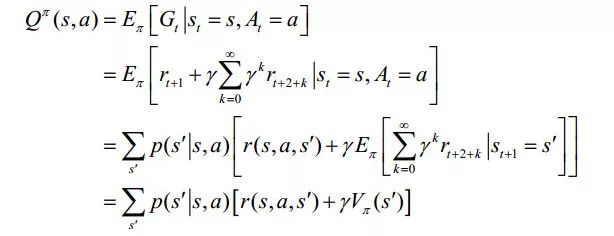
同樣被稱為動作‐值函數的Bellman方程。

類似的給出了相應的最優值函數為：

1. 最優值函數V*（s）是所有策略上的最大值函數：

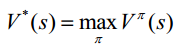
2. 最優行為值函數Q*（s，a）是在所有策略上的最大行為值函數：

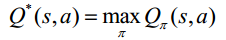
從而的到Bellman最優方程：

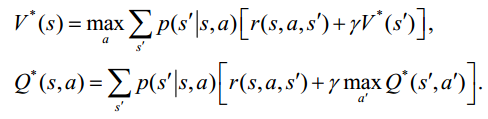
及對應的最優策略：

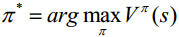
陳教授介紹了求解強化學習的方法，可分為如下兩種情況：

模型已知的方法：動態規劃模型未知的方法：蒙特卡洛方法，時間差分算法

陳教授進一步主要介紹了時間差分算法中兩種不同的方法： 異策略時間差分算法Q‐learning和同策略時間差分算法Sarsa， 兩者的主要區別在于at+1的選擇上的不同，

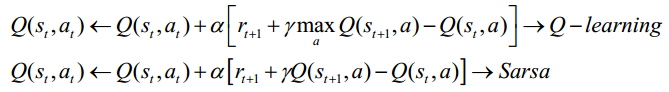
普通的Q‐learning是一種表格方法，適用于狀態空間和動作空間是離散且維數比較低的情況；當狀態空間和動作空間是高維連續的或者出現一個從未出現過的狀態，普通的Q‐learning是無法處理的。為了解決這個問題，陳教授進一步介紹了深度強化學習方法。

深度強化學習

深度強化學習是深度神經網絡與強化學習的結合方法， 利用深度神經網絡逼近值函數，利用強化學習的方法進行更新，根據解決問題思路的不同可分為：

1．基于價值網絡：狀態作為神經網絡的輸入，經過神經網絡分析后，輸出時當前狀態可能執行的所有動作的值函數，即利用神經網絡生成Q值。

2．基于策略網絡：狀態作為神經網絡的輸入，經過神經網絡分析后，輸出的是當前狀態可能采取的動作（確定性策略），或者是可能采取的每個動作的概率（隨機性策略）。

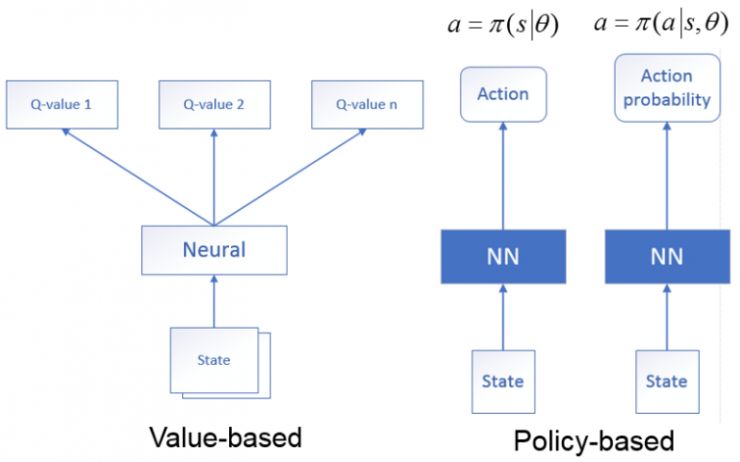
陳教授也提到了Deepmind公司在2013年的Playing Atari with Deep Reinforcement Learning (DRL) 提出的DQN算法，Deep Q‐learning是利用深度神經網絡端到端的擬合Q值，采用Q‐learning算法對值函數更新。DQN利用經驗回放對強化學習過程進行訓練，通過設置目標網絡來單獨處理時間差分算法中的TD偏差。

基于上面內容，陳教授進一步介紹了另外一種經典的時間差分算法，即Actor-Critic的方法，該方法結合了值函數（比如Q learning）和策略搜索算法（Policy Gradients）的優點，其中Actor指策略搜索算法，Critic指Qlearning或者其他的以值為基礎的學習方法，因為Critic是一個以值為基礎的學習法，所以可以進行單步更新，計算每一步的獎懲值，與傳統的PolicyGradients相比提高了學習效率，策略結構Actor，主要用于選擇動作；而值函數結構Critic主要是用于評價Actor的動作，agent根據Actor的策略來選擇動作，并將該動作作用于環境，Critic則根據環境給予的立即獎賞，根據該立即獎賞來更新值函數，并同時計算值函數的時間差分誤差TD-error，通過將TDerror反饋給行動者actor，指導actor對策略進行更好的更新，從而使得較優動作的選擇概率增加，而較差動作的選擇概率減小。

寬度學習

雖然深度結構網絡非常強大，但大多數網絡都被極度耗時的訓練過程所困擾。首先深度網絡的結構復雜并且涉及到大量的超參數。另外，這種復雜性使得在理論上分析深層結構變得極其困難。另一方面，為了在應用中獲得更高的精度，深度模型不得不持續地增加網絡層數或者調整參數個數。因此，為了提高訓練速度，寬度學習系統提供了一種深度學習網絡的替代方法，同時，如果網絡需要擴展，模型可以通過增量學習高效重建。陳教授還強調，在提高準確率方面，寬度學習是增加節點而不是增加層數。基于強化學習的高效性，陳教授指出可以將寬度學習與強化學習結合產生寬度強化學習方法，同樣也可以嘗試應用于文本生成、機械臂抓取、軌跡跟蹤控制等領域。

報告的最后陳教授在強化學習未來會面臨的挑戰中提到了如下幾點：

安全有效的探索

過擬合問題

多任務學習問題

獎勵函數的選擇問題

不穩定性問題