盡管早在上世紀(jì)80年代末,神經(jīng)網(wǎng)絡(luò)就在手寫數(shù)字識(shí)別上表現(xiàn)出色。直到近些年來,隨著深度學(xué)習(xí)的興起,神經(jīng)網(wǎng)絡(luò)才在計(jì)算機(jī)視覺領(lǐng)域呈現(xiàn)指數(shù)級(jí)的增長。現(xiàn)在,神經(jīng)網(wǎng)絡(luò)幾乎在所有計(jì)算機(jī)視覺和圖像處理的任務(wù)中都有應(yīng)用。
相比各種層出不窮的用于計(jì)算機(jī)視覺和圖像處理的新網(wǎng)絡(luò)架構(gòu),這一領(lǐng)域神經(jīng)網(wǎng)絡(luò)的損失函數(shù)相對(duì)而言并不那么豐富多彩。大多數(shù)模型仍然使用L2損失函數(shù)(均方誤差)。然而,L2損失函數(shù)的效果是否真的那么好呢?其他損失函數(shù)表現(xiàn)如何?下面我們將簡單介紹常用的圖像處理損失函數(shù),并比較其在典型圖像處理任務(wù)上的表現(xiàn)。
L1、L2損失函數(shù)
最容易想到的損失函數(shù)的定義,就是逐像素比較差異。為了避免正值和負(fù)值相互抵消,我們可以對(duì)像素之差取絕對(duì)值或平方。
取絕對(duì)值就得到了L1損失函數(shù):
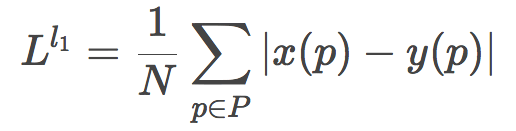
取平方則得到了L2損失函數(shù):
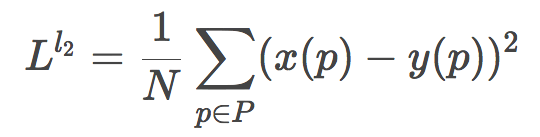
和L1相比,L2因?yàn)槿∑椒降年P(guān)系,會(huì)放大較大誤差和較小誤差之間的差距,換句話說,L2對(duì)較大誤差的懲罰力度更大,而對(duì)較小誤差更為容忍。
除此之外,L1和L2基本上差不多。
實(shí)際上,Nvidia的研究人員Hang Zhao等嘗試過交替使用L1和L2損失函數(shù)訓(xùn)練網(wǎng)絡(luò)(arXiv:1511.08861v3),發(fā)現(xiàn)隨著訓(xùn)練的進(jìn)行,在測試集上的L2損失都下降了。
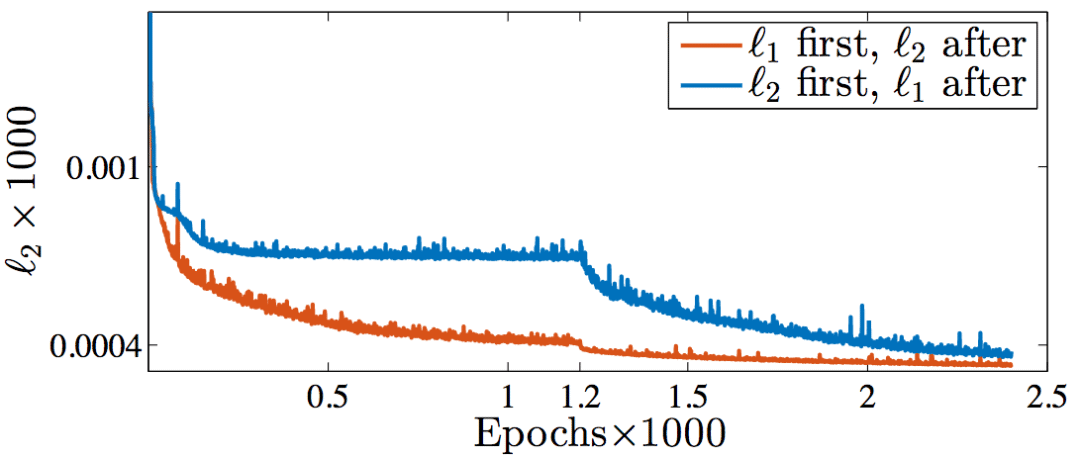
橙:前半段L1、后半段L2;藍(lán):前半段L2、后半段L1
順便提下,從上圖可以看到,前半段L2損失陷入了局部極小值。
不管是L1損失函數(shù),還是L2損失函數(shù),都有兩大缺陷:
假定噪聲的影響和圖像的局部特性是獨(dú)立的。然而,人類的視覺系統(tǒng)對(duì)噪聲的感知受局部照度、對(duì)比、結(jié)構(gòu)的影響。
假定噪聲接近高斯白噪聲,然而這一假定并不總是成立。
SSIM、MS-SSIM損失函數(shù)
為了將人類視覺感知納入考量,可以使用基于SSIM或MS-SSIM的損失函數(shù)。SSIM、MS-SSIM是綜合了人類主觀感知的指標(biāo)。
SSIM(structural similarity,結(jié)構(gòu)相似性)的直覺主要是:人眼對(duì)結(jié)構(gòu)(structure)信息很敏感,對(duì)高亮度區(qū)域(luminance)和“紋理”比較復(fù)雜(contrast)的區(qū)域的失真不敏感。MS-SSIM(Multi-Scale SSIM,多尺度SSIM)則額外考慮了分辨率這一主觀因素(例如,高分辨率的視網(wǎng)膜顯示器上顯而易見的失真,在低分辨率的手機(jī)上可能難以察覺)。
相應(yīng)地,基于SSIM的損失函數(shù)的定義為:
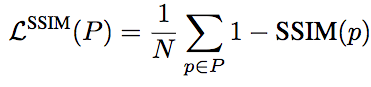
不過,由于損失函數(shù)通常配合卷積網(wǎng)絡(luò)使用,這就意味著計(jì)算損失函數(shù)的時(shí)候其實(shí)只用計(jì)算中央像素的損失,即:
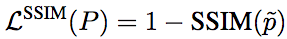
通過上述中央像素?fù)p失函數(shù)訓(xùn)練所得的卷積核,仍將應(yīng)用于圖像中的每個(gè)像素。
同理,基于MS-SSIM的損失函數(shù)為:
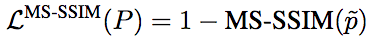
另外,我們知道,損失函數(shù)除了要準(zhǔn)確地表達(dá)模型的目標(biāo)之外,還需要是可微的,這樣才能通過基于梯度下降的方法在反向傳播階段訓(xùn)練。顯然,L1和L2是可微的。
事實(shí)上,基于SSIM和MS-SSIM的損失函數(shù)也同樣是可微的。這里省略具體的推導(dǎo)過程,直接給出結(jié)論。
對(duì)基于SSIM的損失函數(shù)而言:
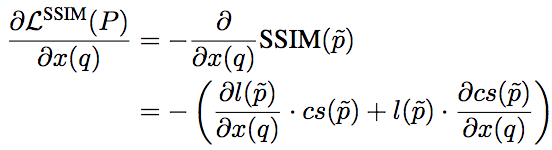
其中,l和cs分別為SSIM的第一項(xiàng)和第二項(xiàng),其梯度為:
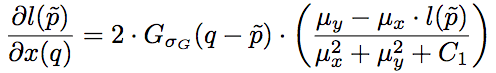
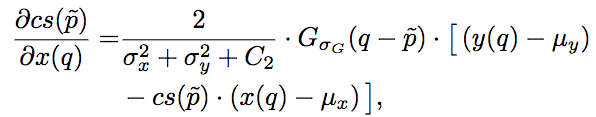
其中,Gσ_G為像素的高斯系數(shù)。這里我們看到,盡管之前的損失函數(shù)只考慮了中央像素,但因?yàn)樵谟?jì)算梯度的時(shí)候,實(shí)際上需要像素的高斯系數(shù),因此誤差仍然能夠反向傳播至所有像素。
相應(yīng)地,基于MS-SSIM的損失函數(shù)的梯度計(jì)算公式為:
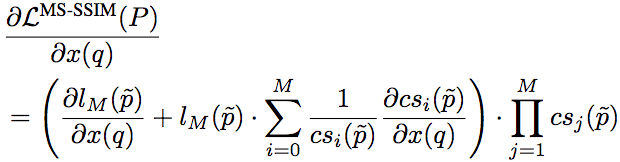
不過,由于基于MS-SSIM的損失函數(shù)需要在每個(gè)尺度上都重復(fù)算一遍梯度,會(huì)大大拖慢訓(xùn)練速度(每一次迭代都相當(dāng)于M次迭代),因此實(shí)踐中往往轉(zhuǎn)而采用某個(gè)逼近方法計(jì)算。例如,使用M組不同的Gσ_G值作為替代,每組值為前一組的1/2.
評(píng)測
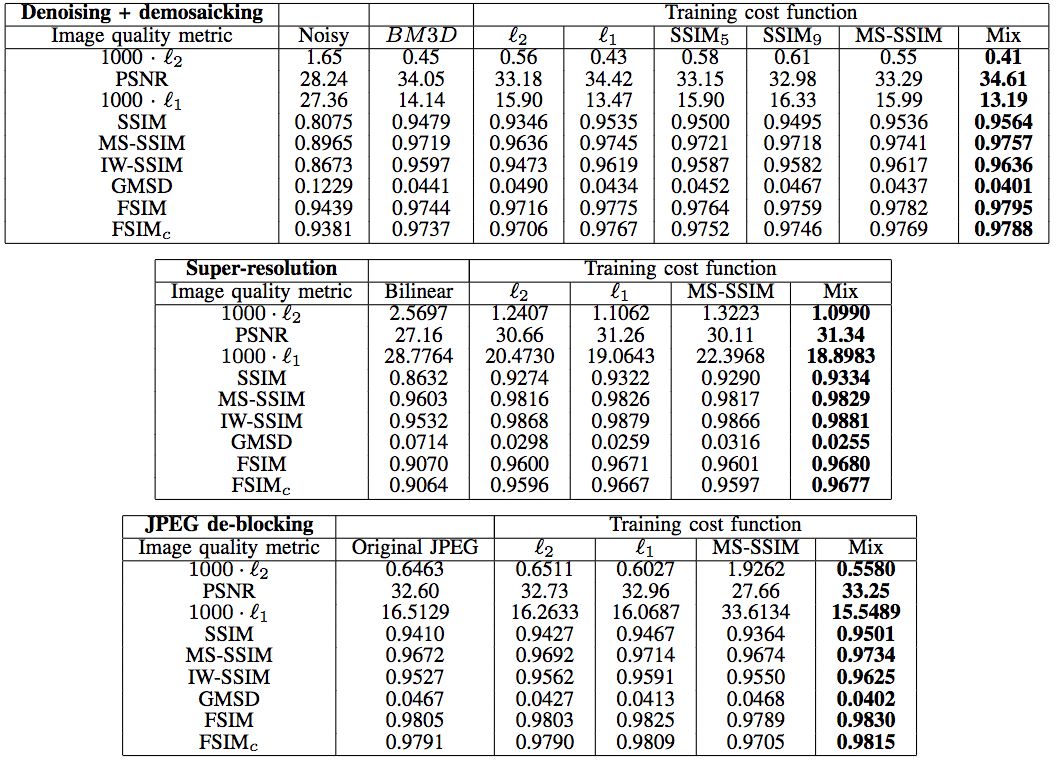
Hang Zhao等在JPEG去噪、去馬賽克,超分辨率重建,JPEG去區(qū)塊效應(yīng)等場景對(duì)比了不同損失函數(shù)的效果。
去噪、去馬賽克
上圖中的BM3D代表CFA-BM3D,為當(dāng)前最先進(jìn)的降噪算法。我們看到,在天空這樣的平坦區(qū)域(d),L2損失函數(shù)出現(xiàn)了污跡失真(splotchy artifact)。
超分辨率
仔細(xì)觀察下圖蝴蝶翅膀的黑帶處,可以看到L2出現(xiàn)了光柵失真(grating artifacts)。
同樣,下圖女孩的面部,也可以觀察到L2的光柵失真。
去區(qū)塊
仔細(xì)觀察建筑物邊緣的區(qū)塊,可以看到L1比L2去區(qū)塊效果要好。
天空區(qū)域的區(qū)塊效應(yīng)更明顯,相應(yīng)地,L1在去區(qū)塊方面表現(xiàn)優(yōu)于L2這點(diǎn)就更明顯了。
更多去區(qū)塊的例子印證了我們上面的觀察。
混合損失函數(shù)
你應(yīng)該已經(jīng)注意到了,上面的對(duì)比圖中有一個(gè)“Mix”,而且事實(shí)上它是看起來效果最好的那個(gè)。這個(gè)“Mix”其實(shí)是Hang Zhao等提出的混合了MS-SSIM和L1得到的損失函數(shù):
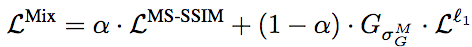
這個(gè)混合損失函數(shù)的定義很簡單,基本上就是MS-SSIM和L1的加權(quán)和,只不過因?yàn)镸S-SSIM反向傳播誤差時(shí)需要用到G高斯分布參數(shù),因此在L1部分也分素相乘相應(yīng)的分布參數(shù)而已。
Hang Zhao等經(jīng)過一些試驗(yàn),將α定為0.84,使兩部分損失的貢獻(xiàn)大致相等(試驗(yàn)發(fā)現(xiàn),α的微小變動(dòng)對(duì)結(jié)果的影響不顯著)。
以上我們已經(jīng)從視覺上演示了MS-SSIM+L1混合損失函數(shù)效果最佳。定量測試也表明,在多種圖像處理任務(wù)上,基于多種圖像質(zhì)量指標(biāo),總體而言,混合損失函數(shù)的表現(xiàn)最好。
網(wǎng)絡(luò)架構(gòu)
上述試驗(yàn)所用的網(wǎng)絡(luò)架構(gòu)為全卷積神經(jīng)網(wǎng)絡(luò)(CNN):
輸入為31x31x3.
第一個(gè)卷積層為64x9x9x3.
第二個(gè)卷積層為64x5x5x64.
輸出卷積層為3x5x5x64.
內(nèi)卷積層的激活函數(shù)為PReLU。
數(shù)據(jù)集
訓(xùn)練集取自MIT-Adobe FiveK數(shù)據(jù)集,共700張RGB圖像,尺寸調(diào)整為999x666. 測試集取自同一數(shù)據(jù)集,共40張圖像。
結(jié)語
總結(jié)一下以上評(píng)測:
在很多場景下,L2損失函數(shù)的表現(xiàn)并不好。有時(shí)可以嘗試下同樣簡單的L1損失函數(shù),說不定能取得更好的效果。
由于未考慮到主觀感知,很多場景下,基于SSIM或MS-SSIM的損失函數(shù)能取得比L1、L2更好的效果。
結(jié)合MS-SSIM和L1通常會(huì)有奇效。
總之,雖然L2損失函數(shù)是用于圖像處理的神經(jīng)網(wǎng)絡(luò)事實(shí)上的標(biāo)準(zhǔn),但也不可迷信,不假思索地選用L2可能會(huì)錯(cuò)過更優(yōu)的選擇。
-
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4771瀏覽量
100772 -
函數(shù)
+關(guān)注
關(guān)注
3文章
4331瀏覽量
62622 -
cnn
+關(guān)注
關(guān)注
3文章
352瀏覽量
22215
原文標(biāo)題:CNN圖像處理常用損失函數(shù)對(duì)比評(píng)測
文章出處:【微信號(hào):jqr_AI,微信公眾號(hào):論智】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
對(duì)象檢測邊界框損失函數(shù)–從IOU到ProbIOU介紹
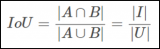
TensorFlow損失函數(shù)(定義和使用)詳解
keras常用的損失函數(shù)Losses與評(píng)價(jià)函數(shù)Metrics介紹
神經(jīng)網(wǎng)絡(luò)中的損失函數(shù)層和Optimizers圖文解讀
機(jī)器學(xué)習(xí)經(jīng)典損失函數(shù)比較
機(jī)器學(xué)習(xí)實(shí)用指南:訓(xùn)練和損失函數(shù)
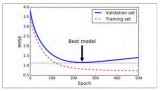
三種常見的損失函數(shù)和兩種常用的激活函數(shù)介紹和可視化
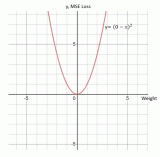
深度學(xué)習(xí)的19種損失函數(shù)你了解嗎?帶你詳細(xì)了解
計(jì)算機(jī)視覺的損失函數(shù)是什么?
損失函數(shù)的簡要介紹
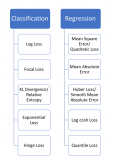
機(jī)器學(xué)習(xí)和深度學(xué)習(xí)中分類與回歸常用的幾種損失函數(shù)
表示學(xué)習(xí)中7大損失函數(shù)的發(fā)展歷程及設(shè)計(jì)思路
訓(xùn)練深度學(xué)習(xí)神經(jīng)網(wǎng)絡(luò)的常用5個(gè)損失函數(shù)

語義分割25種損失函數(shù)綜述和展望





 L2損失函數(shù)的效果是否真的那么好呢?其他損失函數(shù)表現(xiàn)如何?
L2損失函數(shù)的效果是否真的那么好呢?其他損失函數(shù)表現(xiàn)如何?










評(píng)論