編者按:在機器學習面前,我們都像一個孩子。當剛學會反向傳播算法時,許多人會不滿足于最基礎的感知器,去嘗試搭建更深、層數更多的神經網絡。他們欣賞著自己的實現,就像沙灘上的孩子驕傲地看著自己用泥沙堆起來的城堡。但和城堡的徒有其表一樣,這些神經網絡的性能往往也難以令人滿意,它們也許會陷入無休止的訓練,也許準確率永遠提不上來。這時,一些人就會開始懷疑:難道神經網絡不是最先進的技術?
類似的懷疑,誰都有過——
神經網絡的訓練過程包括前向傳播和反向傳播兩個部分,如果前向傳播得到的預測結果和實際結果不符,這就說明網絡沒有訓練好,要用反向傳播去重新調整各個權重。這之中涉及各種常見的優化算法,以梯度下降為例,它的思路是把當前梯度的負值方向作為搜索方向,通過調整權重使目標函數趨近局部最小值,也就是讓代價函數/損失函數越來越小。
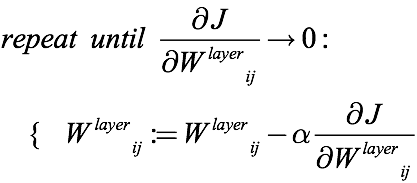
如上式所述,梯度下降算法用原權重減去乘上標量α(0到1之間)的梯度來更新權重,并“重復”這一過程直至收斂。但在實際操作中,這個“重復”的迭代次數是一個人為選定的超參數,這意味著它可能過小,最后收斂效果并不好;它也可能過大,網絡被訓練得“沒完沒了”。因此訓練時間和訓練效果之間存在“過猶不及”的尷尬情況。
那么這個超參數是怎么影響收斂的?就像不同人下山速度不同一樣,梯度下降有一個下降步長,迭代時間越短,步長就越大,雖然收斂速度很快,但它容易無法精確收斂到最后的最優解;相反地,如果迭代時間過長,步長越小,那在很長一段收斂過程中,可能網絡的權重并不會發生太大改變,而且相對大步長,小步長在規定迭代次數內接近最小值也更難。

小步長收斂宛如“蝸牛”
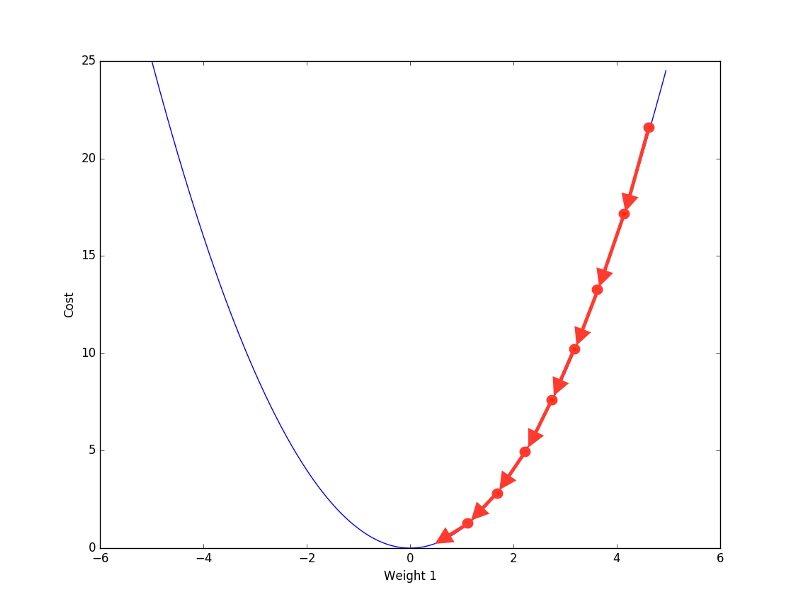
大步長收斂效率更高
這還不是唯一的毛病,當梯度數值過小時,它容易被四舍五入為0,也就是下溢出。這時再對這個數做某些運算就會出問題。
看到這里,我們似乎已經得到這樣一個事實:小梯度 = 不好。雖然這個結論看起來有些武斷,但在很多情況下,它并不是危言聳聽,因為本文要講的梯度消失就是由小梯度引起的。
讓我們回想一下sigmoid函數,這是一個經常會在分類問題中遇到的激活函數:
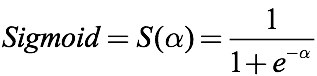
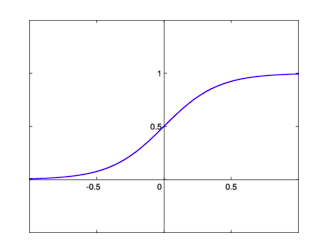
如上圖所示,sigmoid的作用確實是有目共睹的,它能把任何輸入的閾值都限定在0到1之間,非常適合概率預測和分類預測。但這幾年sigmoid與tanh卻一直火不起來,凡是提及激活函數,大家第一個想到的就是ReLU,為什么?
因為sigmoid幾乎就是梯度消失的代名詞,我們先對它求導:
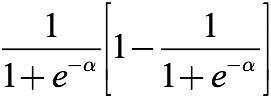
這看起來就是個很普通的 s(1-s) 算式,好像沒什么問題。讓我們繪制它的圖像:
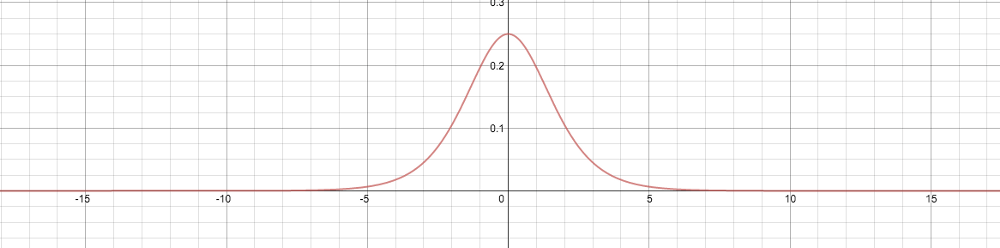
仔細看一看,還是沒問題嗎?可以發現,上圖中最大值只有1/4,最小值無限接近0,換言之,這個導數的閾值是(0, 1/4]。記住這個值,待會兒我們會用到。
現在我們先回頭繼續討論神經網絡的反向傳播算法,看看梯度對它們會產生什么影響。

這是一個最簡單的神經網絡,除了輸入神經元,其他神經元的act()都來自前一層的神經元:先用act()乘上一個權重,再經激活函數饋送進下一層,來自上層的信息就成了一個全新的act()。最后的J歸納了前饋過程中的所有誤差項(error),輸出網絡整體誤差。這之后,我們再執行反向傳播,通過梯度下降修改參數,使J的輸出最小化。
下面是第一項權重w1的導數:

我們可以利用權重的導數來進行梯度下降,繼而迭代出全局最優點,但在那之前,這個派生的乘法運算值得關注:
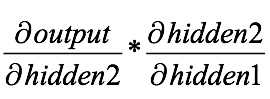
由于上一層的輸出乘上激活函數就是下一層的輸入,所以上式其實還包含sigmoid的導數,如果把信息全部表示完整,從輸出返回到第二層隱藏層的表達式應該是:
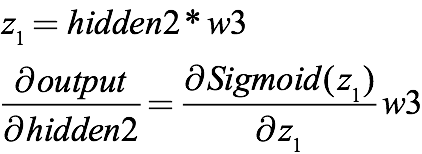
同理,從第二層隱藏層到第一層隱藏層則是:
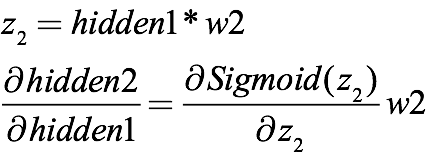
它們都包含sigmoid函數,合起來就是:
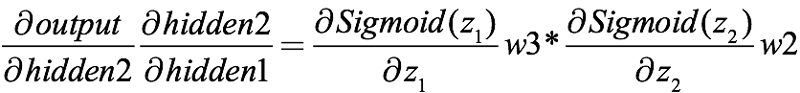
之前我們已經對sigmoid求過導了,計算出它的閾值是(0, 1/4]。結合上式,兩個0到1之間的小數相乘,積小于任一乘數。而在典型的神經網絡中,權重初始化的一般方法是權重的選擇要服從均值=0,方差=1的正態分布,因此這些初始權重的閾值是[-1, 1]。
接下來的事情就很清楚了:
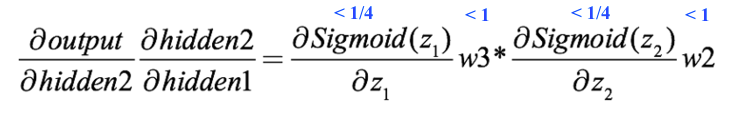
即便不用常規權重初始化方法,w2和w3大于1,但它們對兩個sigmoid導數相乘來說還是杯水車薪,梯度變得太小了。而在實際操作中,隨機權重是很可能小于1的,所以那時它反而是在助紂為虐。
這還只有2個隱藏層,試想一下,如果這是一個工業級的深層神經網絡,那么當它在執行反向傳播時,這個梯度會變得有多小,小到突然消失也在情理之中。另一方面,如果我們把然激活函數導數的絕對值控制在大于1,那這個連乘操作也很嚇人,結果會無限大,也就是我們常說的“梯度爆炸”。
現在,我們來看一個典型的ANN:
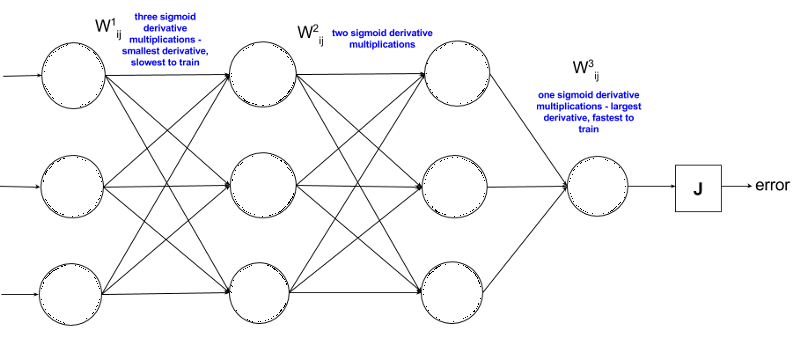
第一項權重距離誤差項J最遠,因此求導后它的表達式最長,也包含更多sigmoid函數,計算結果更小。所以神經網絡的第一層往往是訓練時間最長的一層。它同時也是后面所有層的基礎,如果這一層不夠準確,那就會產生連鎖反應,直接拉低整個網絡的性能。
這就也是神經網絡,尤其是深層神經網絡一開始并不為行業所接受的原因。正確訓練前幾層是整個網絡的基礎,但激活函數的缺陷和硬件設備的算力不足,使當時的研究人員連打好基礎都做不到。
看到這里,我們應該都已經理解sigmoid函數的缺點了,它的替代方案tanh函數雖然也曾聲名大噪,但考慮到tanh(x)=2sigmoid(2x)-1,它肯定也存在同樣的問題。那么,現在大家都在用的ReLU好在哪兒?
首先,ReLU是一個分段函數:
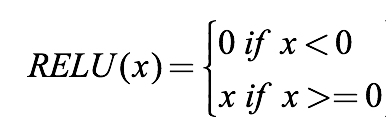
它還有另一種寫法:
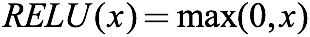
當輸入小于0時,函數輸出0;當輸入大于零時,函數輸出x。
我們計算它的導數來對比sigmoid:
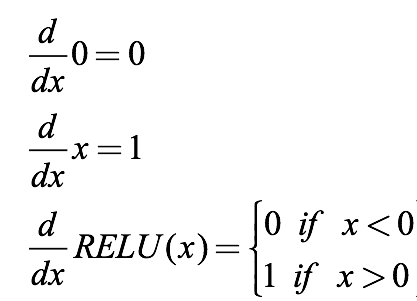
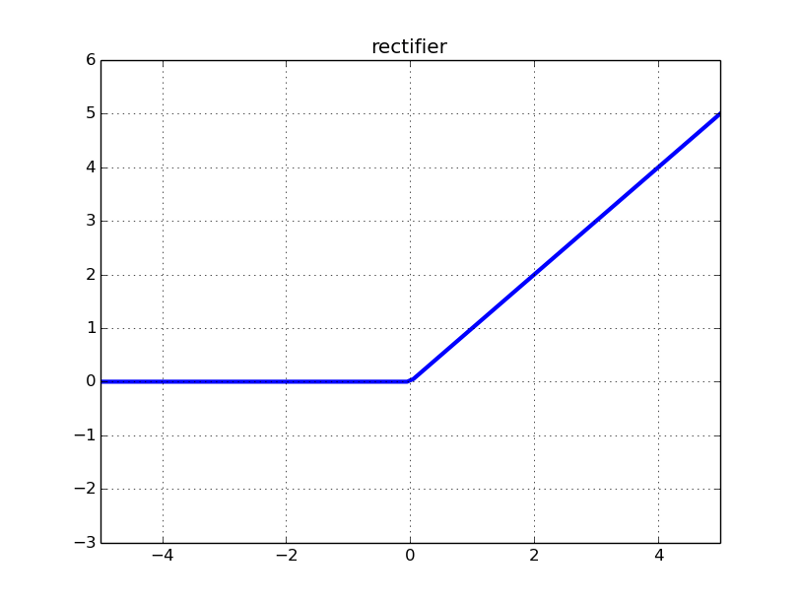
然后是它的圖像,注意一點,它在0點不可微,所以當x=0時,圖中y軸上應該是兩個空心圓。
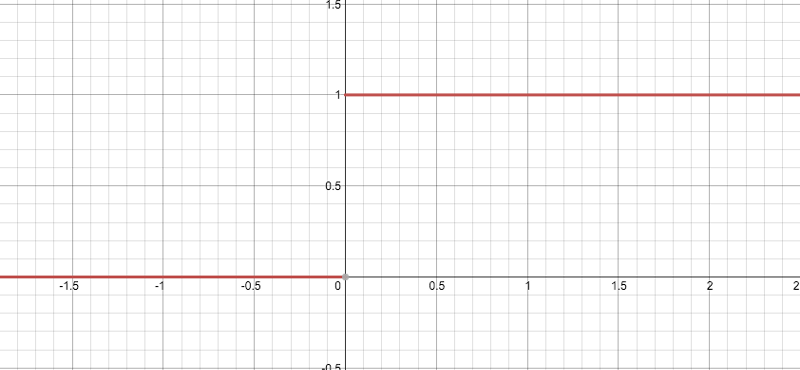
可以發現,導數的閾值終于不再是(0, 1)了,它好像可以避免梯度消失,但似乎又有點不對勁?當我們把一個負值輸入到ReLU函數后,梯度為0,這時這個神經元就“壞死”了。換句話說,如果存在負數權重,那某些神經元可能永遠不會被激活,導致相應參數永遠不會被更新。從某種意義上來說,ReLU還是存在部分梯度消失問題。
那么,我們該怎么選擇呢?不急,這里還有一種激活函數——Leakly ReLU。
既然ReLU的“梯度消失”源于它的閾值0,那么我們可以把它重設成一個0到1之間的具體小數。這之后,當輸入為負時,它還是具有非常小的梯度,這就為網絡繼續學習提供了機會。
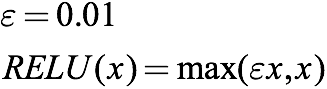
上式中的ε=0.01,但它最常見的范圍是0.2-0.3。因為斜率小,輸入負值權重后,它在圖像上是一條非常緩的線:
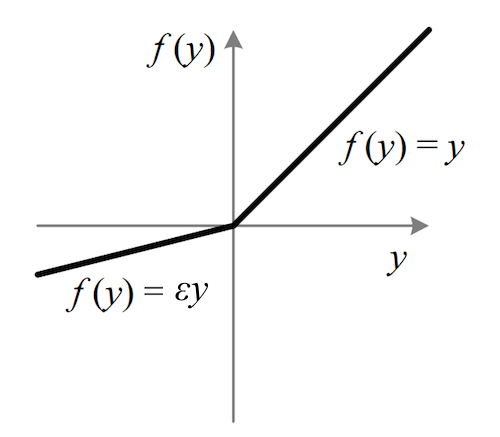
這里我們要聲明一點:雖然Leakly ReLU可以解決ReLU的神經元壞死問題,但它的表現并不一定比ReLU更好。比如常數ε萬一過小,它就很可能會導致新的梯度消失。另一方面,這兩個激活函數有個共同的缺點,即不像tanh和sigmoid一樣輸出有界,如果是在RNN這樣很深的神經網絡里,即便ReLU的導數是0或1,很小,但除了它我們還有那么多權重,多項連乘會導致非常大的輸出值,然后梯度就爆炸了。
所以總的來說,ReLU并沒有根治梯度消失這個問題,它只是在一定程度上緩解了矛盾,并產生了另一個新問題。這也是這些激活函數至今還能共存的原因——CNN用ReLU更常見,而RNN大多用tanh。在“玄學”的大背景下,這大概是新手入門機器學習后,接觸到的第一起trade off吧。
-
神經網絡
+關注
關注
42文章
4777瀏覽量
100974 -
梯度
+關注
關注
0文章
30瀏覽量
10333 -
深度學習
+關注
關注
73文章
5511瀏覽量
121355
原文標題:深度學習解密:我的梯度怎么消失了?
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
詳解深度學習、神經網絡與卷積神經網絡的應用





 一些人會懷疑:難道神經網絡不是最先進的技術?
一些人會懷疑:難道神經網絡不是最先進的技術?

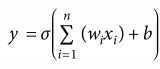










評論