如何找出數據集的基礎結構?如何聚類和建立最有效的分組?如何在壓縮格式后有效地表達數據?這些都是無監督學習的目標。它是“無監督”的——因為你是從未經標記的數據開始的(沒有Y)。
在這篇文章中,我們要探討的無監督學習任務主要有兩個,一是通過相似性把數據聚類成組,二是以降低維度的方式壓縮數據,同時保持其結構和可用性。
無監督學習可能涉及的場景:
某廣告平臺把美國消費者細分為有類似購物習慣的較小群體,以便更精準地向他們投放廣告;
Airbnb將根據社區對住房列表進行分組,以便用戶能更簡便地進行查詢;
數據科學研究團隊降低大型數據集的維度,以簡化模型和控制文件大小。
與監督學習相比,我們無法提前預測無監督學習算法的具體效果,它的“表現”往往是主觀的,只面向特定領域。
聚類
在現實世界中,聚類的一個典型案例是市場數據提供商Acxiom的系統Personicx,它把美國家庭分為21個生活水平群體,又在其下細分出79類不同群組。也許這看起來并沒有多大用處,但對于廣告商來說,這些數據成了他們在Facebook上確定廣告投放地區、時間段的重要依據。

Personicx人口聚類
在白皮書中,Acxiom稱系統使用的聚類方法是質心聚類和主成分分析,之后我們會對它們做簡要介紹。
你可以想象,這些數據精準地切合了廣告商的需求。對于迫切希望通過推送廣告來達到立竿見影效果的廣告商而言,他們重視的內容有兩個:一是了解目標消費者的群體大小;二是通過針對消費者的人口統計特征,如興趣愛好和生活方式,挖掘潛在的新客戶。

Acxiom有一個名為“我的聚類是什么”的小工具,只需回答幾個簡單問題,你就能知道算法對你的分類
讓我們先從聚類算法開始,慢慢了解他們是怎么做的。
k-means聚類
聚類是一種涉及數據點分組的機器學習技術。給定一組數據點,我們可以用聚類算法將每個數據點到分類到圖像中的特定組中。理論上,同一組中的數據點應具有相似的屬性和特征,而不同組中的數據點的屬性和特征則應高度不同。
通過k-means算法,我們能把目標數據點聚類為k個簇。k值越大,簇越少,每一簇包含的數據點就越多;k值越小,簇越多,每一簇包含的數據點就越少。
該算法的輸出是一堆打好了“標簽”的數據點,每個標簽指向數據點所屬的k簇。進行聚類時,算法會根據k值為數據定義k個聚類質心點,這些質心就像是每個簇的核心,它們不斷“捕捉”最接近自己的點并把它們添加進聚類中。
如果這還不夠形象,那你也可以把它們想成派對舞會上出現的那些充滿魅力的人,他們瞬間就能引起身邊人的關注。如果這樣的人只有一個,那全場人都會聚集在他身邊;如果有很多個,那舞會上就會形成許多較小的活動團體。
以下是k-means聚類的簡要步驟:
1. 定義k個質心。隨機初始化k個質心;
2. 為質心找到最接近它的數據點并構建簇。將每個數據點分配給k個質心中的一個,分配依據是數據點和質心的接近程度,也就是歐氏距離平方和最小。
3. 更新質心位置,將它移到更新后簇的中心。計算簇中所有點的平均位置,這個得出的新向量就是質心的新位置。

k-means聚類的一個實際應用是對手寫數字進行分類。假設我們有一些黑白的數字圖像,圖像的像素為64 × 64,每個像素代表一個維度,那么這些圖像就有64 × 64 = 4,096個維度。在這個4,096維的空間中,k-means算法能把所有聚集緊密的像素點聚類成一個簇,假設它們同屬于一個數字。實踐證明,這種做法在數字識別上取得了非常好的結果。
層次聚類
層次聚類和常規的聚類算法大體相似,它的不同之處在于它聚類的簇具有層次結構。這對于一些有不同靈活性需求的任務來說很有用,如想象一下Amazon的網上商城,它的主頁上有很多分組的商品,通過導航欄,我們能找到目標商品所屬的大類,之后再是更細分的、更具體的小類。對于一些項目集群,像這樣逐層提高數據顆粒密度是有價值的。
就算法的輸出而言,除了聚類成各個子集,層次聚類的一個優點是可以呈現一整棵樹,并由你自行選擇要聚類成什么效果,比如簇的數量。
以下是參差聚類的簡要步驟:
1. 定義N個簇,每個簇包含1個數據點;
2. 合并彼此最接近的兩個簇,現在我們就有N-1個簇;
3. 重新計算各簇之間的距離。對于計算距離,我們有多種方法,其中一種是將兩個簇之間的距離視為他們各自數據點之間的平均距離。
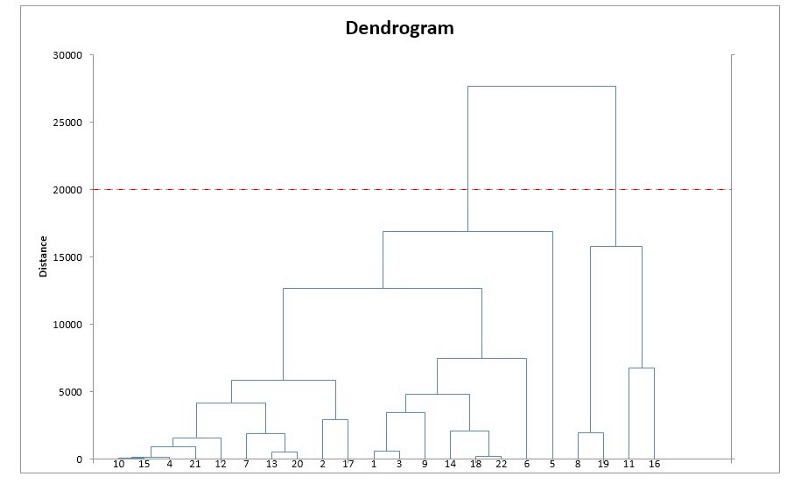
4. 重復步驟2和3,直到最后獲得一個包含所有數據點的簇。這時我們得到了一棵樹,如下圖所示。
5. 選取多個簇并在樹狀圖上繪制一條水平線。例:如果我們想要k = 2個簇,那就應該在distance = 20000的位置畫一條線,這時我們就能得到一個包含數據點8、9、11、16的簇以及另一個簇。簇的數量等于水平線和樹狀圖的交點數。
降維
降維聽起來和壓縮差不多。它是為了盡量減少數據的復雜性,同時保持盡可能多的相關結構。如果我們有一張128 × 128 × 3的圖像(長×寬×RGB),它的數據維度就是49,152。這時,如果我們能在不破壞圖象原有內容的前提下降低圖像所在空間的維度,這對于后續計算是十分有幫助的。
讓我們先通過實踐看看兩種用于降維的主要方法:主成分分析和奇異值分解。
主成分分析(PCA)
在開始講解前,我們先來做一個線性代數小復習——向量空間和基。
在一個普通的平面坐標中,原點O是(0, 0),基向量i為(1, 0),j為(0, 1)。但事實證明,我們可以選擇一個完全不同的基,比如把i'=(2, 1)和j'=(1, 2)作為基向量,這就成了另一個坐標系。如果你有耐心,你可以計算出原來iOj坐標系上的(2, 2)到i'Oj'上會變成(6, 6)。
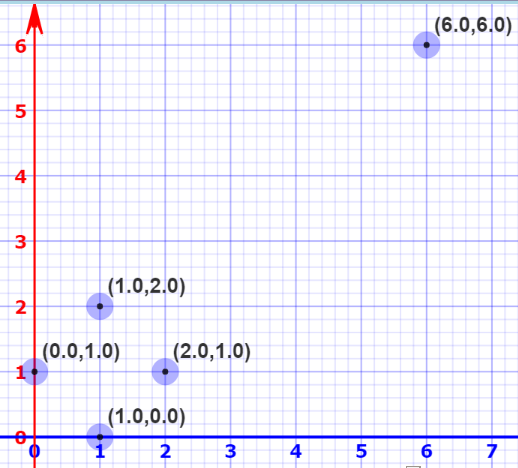
這樣做的意義在于我們能改變向量空間的基,想象更高維的空間,比如5萬維。選擇一個基,挑選出其中最重要的200個基向量,我們把這些向量稱之為“主成分”。這之后,你挑出的向量子集就能構成一個新的向量空間,它的維度比原來的更低,但保留了大部分數據復雜性。
選擇最重要的主成分,考察它保留了多少差異性,然后按照這個指標進行排序。
PCA的另一個用處在于降低數據文件大小。經過重新映射后,原本的數據空間會被壓縮至低維,更有利于之后的計算。
擴展閱讀:Diffusion Mapping and PCA on the WikiLeaks Cable Database
地址:http://mou3amalet.com/cargocollective/675_xuesabri-final.pdf
奇異值分解(SVD)
讓我們將數據表示為一個較大的A = m × n的矩陣。SVD是一種計算,它允許我們將該大矩陣分解為3個較小矩陣(U = m × r,對角矩陣Σ= r × r,以及V = r × n,其中r是一個小數)的乘積。
以下是一個直觀的例子。
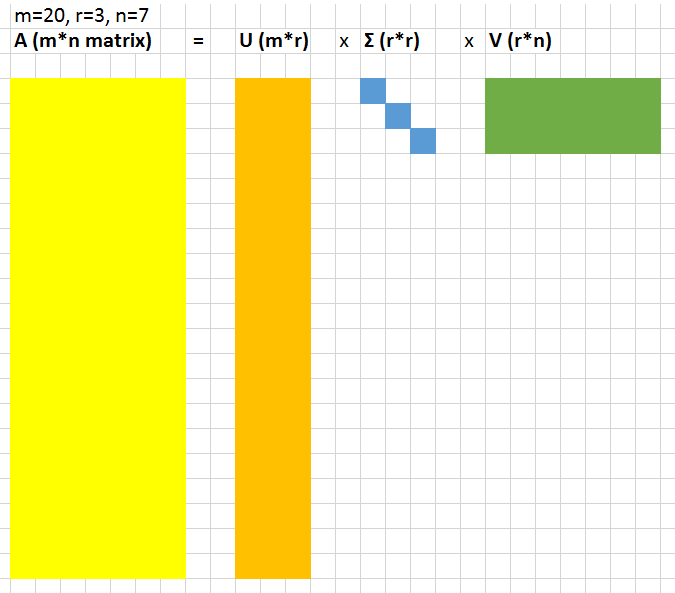
r*r對角矩陣Σ中的值被稱為奇異值。它們的神奇之處在于可以用來壓縮原始矩陣。如果我們在原始矩陣U和V中刪除最小的20%奇異值的相關列,矩陣會縮小很多,但仍能很好地表示底層矩陣。為了更準確地展示它的效果,我們可以來看看這條狗:
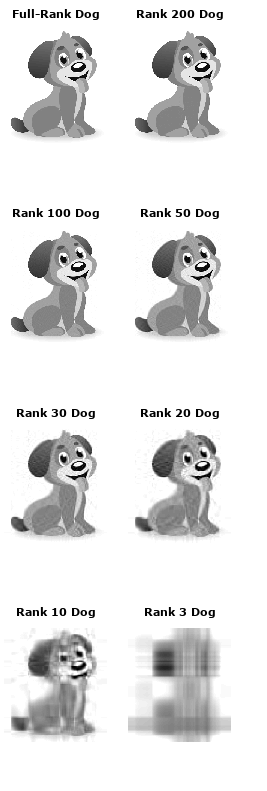
首先,如果我們按照量級對奇異值(矩陣Σ的值)進行排序,則前50個奇異值包含整個矩陣Σ85%的量值。
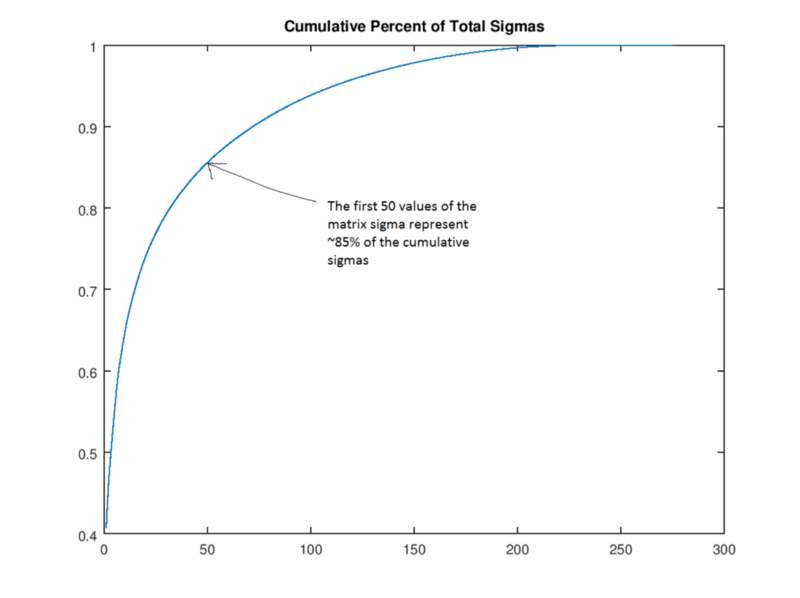
因此我們可以把矩陣Σ中剩下的250個值舍去,也就是設置為0,獲得一個“rank 50”的版本。在下圖中,我們分別列舉了200、100、50、30、20、10和3的狗,可以看出,隨著圖片空間逐漸變小,它的清晰度也不斷下降,但就肉眼的觀察情況看,“rank 30”的圖像還是表現出了很多接近原圖的特征。我們可以計算這一過程中算法壓縮了多少空間:原始圖像矩陣有305 × 275 = 83,875個值;“rank 30”的狗則只有305 × 30 + 30 + 30 × 275 = 17,430個值(要算上矩陣U和V乘以0的量)——幾乎是原圖的五分之一。
實戰演練和進階閱讀
k-means聚類
嘗試可視化聚類過程,以建立對算法工作原理更直觀的理解。你也可以參考用k-means聚類手寫數字的開源項目,并學習坐著列出的各類在線教程。
-
聚類
+關注
關注
0文章
146瀏覽量
14229 -
K-means
+關注
關注
0文章
28瀏覽量
11329 -
數據集
+關注
關注
4文章
1209瀏覽量
24802
原文標題:《Machine Learning for Humans》第五章:無監督學習
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
基于模糊分組和監督聚類的RBF回歸性能改進
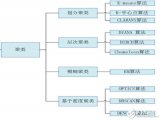
常用聚類算法有哪些?六大類聚類算法詳細介紹




 如何找出數據集的基礎結構?如何聚類和建立最有效的分組?
如何找出數據集的基礎結構?如何聚類和建立最有效的分組?










評論