現代的深度神經網絡通常具有海量參數,甚至高于訓練數據的大小。這就意味著,這些深度網絡有著強烈的過擬合傾向。緩解這一傾向的技術有很多,包括L1、L2正則、及早停止、組歸一化,以及dropout。在訓練階段,dropout隨機丟棄隱藏神經元及其連接,以打破神經元間的共同適應。盡管dropout在深度神經網絡的訓練中取得了巨大的成功,關于dropout如何在深度學習中提供正則化機制,目前這方面的理論解釋仍然很有限。
最近,約翰·霍普金斯大學的Poorya Mianjy、Raman Arora、Rene Vidal在ICML 2018提交的論文On the Implicit Bias of Dropout,重點研究了dropout引入的隱式偏置。
基于權重系聯的線性自動編碼器
為了便于理解dropout的作用機制,研究人員打算在簡單模型中分析dropout的表現。具體而言,研究人員使用的簡單模型是只包含一個隱藏層的線性網絡。該網絡的目標是找到最小化期望損失(平方損失)的權重矩陣U、V:
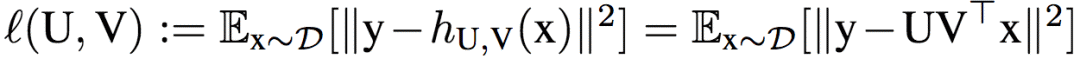
上式中,x為輸入,y為標注輸出,D為輸入x的分布,h表示隱藏層。
學習算法為帶dropout的隨機梯度下降,其目標為:
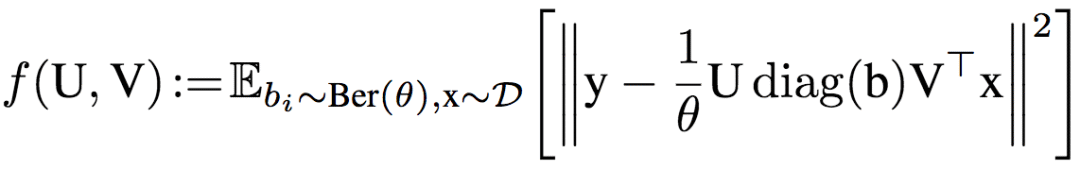
其中,dropout率為1-θ,具體的算法為:

這一算法的目標等價于(推導過程見論文附錄A.1):
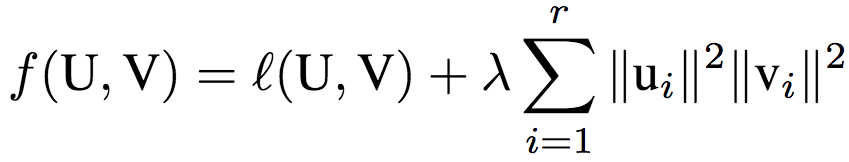
其中,λ = (1-θ)/θ
研究人員又令U = V,進一步簡化模型為權重系聯的單隱藏層線性自動編碼器。相應地,該網絡的目標為:
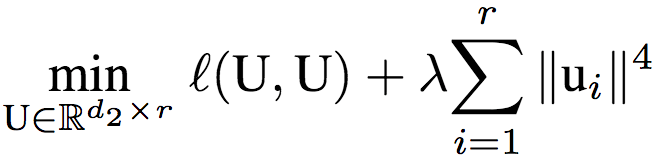
研究人員證明了,如果矩陣U是以上目標的全局最優解,那么U的所有列范數相等。這意味著,dropout傾向于給所有隱藏節點分配相等的權重,也就是說,dropout給整個網絡加上了隱式的偏置,傾向于讓隱藏節點都具有類似的影響,而不是讓一小部分隱藏節點具有重要影響。
上圖可視化了參數λ的不同取值的效果。該網絡為單隱藏層線性自動編碼器,搭配一維輸入、一維輸出,隱藏層寬度為2。當λ = 0時,該問題轉換為平方損失最小化問題。當λ > 0時,全局最優值向原點收縮,所有局部極小值均為全局最小值(證明過程見論文第4節)。當λ增大時,全局最優值進一步向原點收縮。
單隱藏層線性網絡
接著,研究人員將上述結果推廣到了單隱藏層線性網絡。回憶一下,這一網絡的目標為:
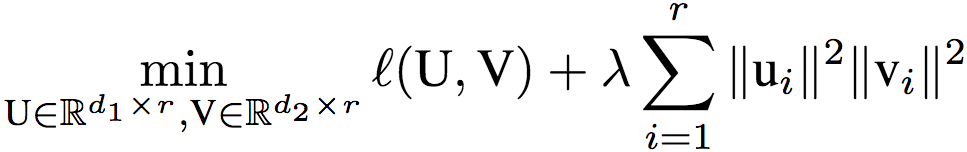
和權重系聯的情形類似,研究人員證明了,如果矩陣對(U, V)是以上目標的全局最優解,那么,‖ui‖‖vi‖ = ‖u1‖‖v1‖,其中,i對應隱藏層的寬度。
研究人員進一步證明,前面提到的單隱藏層線性神經網絡的目標等價于正則化的矩陣分解(regularized matrix factorization):
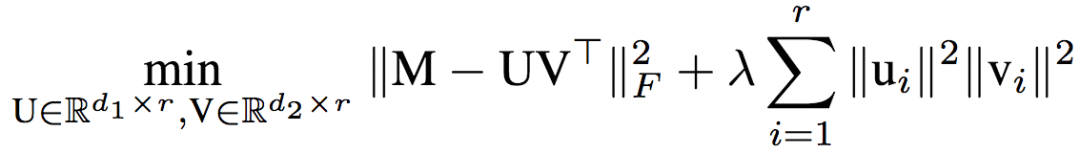
利用矩陣分解這一數學工具,研究人員證明了全局最佳值可以在多項式時間內找到:

試驗
研究人員試驗了一些模型,以印證前面提到的理論結果。
上圖可視化了dropout的收斂過程。和之前的可視化例子類似,模型為單隱藏層線性自動編碼器,一維輸入、一維輸出,隱藏層寬度為2。輸入取樣自標準正態分布。綠點為初始迭代點,紅點為全局最優點。從圖中我們可以看到,在不同的λ取值下,dropout都能迅速收斂至全局最優點。
研究人員還在一個淺層線性網絡上進行了試驗。該網絡的輸入x ∈ ?80,取樣自標準正態分布。網絡輸出y ∈ ?120,由y = Mx生成,其中M ∈ ?120x80均勻取樣自右、左奇異子空間(指數譜衰減)。下圖展示了不同參數值(λ ∈ {0.1, 0.5, 1})與不同隱藏層寬度(r ∈ {20, 80})的組合。藍色曲線為dropout不同迭代次數下對應的目標值,紅線為目標的最優值。總共運行了50次,取平均數。
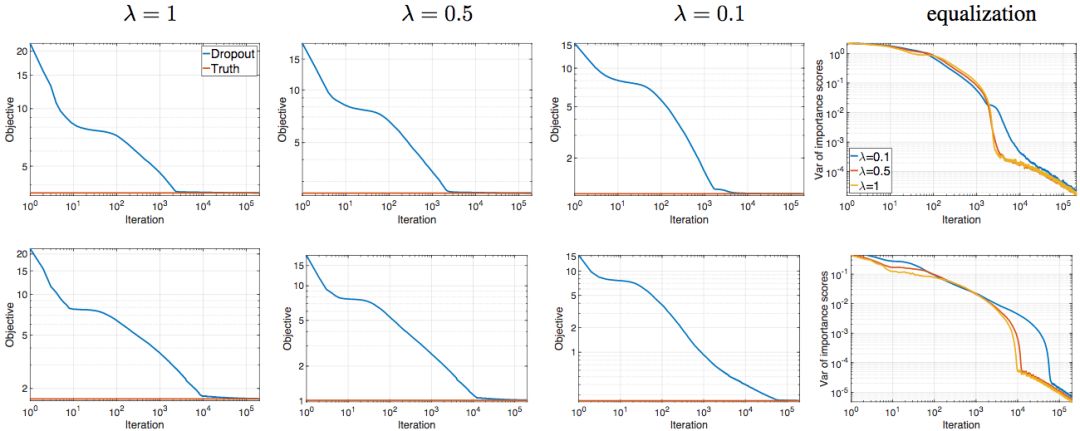
上:r = 20;下:r = 80
上圖最后一列為“重要性評分”的方差。重要性評分的計算方法為:‖uti‖‖vti‖,其中t表示時刻(迭代),i表示隱藏層節點。從上圖我們看到,隨著dropout的收斂,“重要性評分”的方差單調下降,最終降至0. 且λ較大時,下降較快。
結語
這項理論研究確認了dropout是一個均質地分配權重的過程,以阻止共同適應。同時也從理論上解釋了dropout可以高效地收斂至全局最優解的原因。
研究人員使用的是單隱藏層的線性神經網絡,因此,很自然地,下一步的探索方向為:
更深的線性神經網絡
使用非線性激活的淺層神經網絡,例如ReLU(ReLU可以加速訓練)
-
編碼器
+關注
關注
45文章
3650瀏覽量
134756 -
神經網絡
+關注
關注
42文章
4774瀏覽量
100894 -
Dropout
+關注
關注
0文章
13瀏覽量
10054
原文標題:dropout的隱式偏置
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
什么是線性編碼器
稀疏邊緣降噪自動編碼器的方法
基于動態dropout的改進堆疊自動編碼機方法
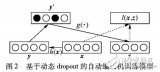
自動編碼器的社區發現算法
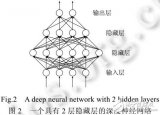
自動編碼器與PCA的比較
如何使用深度神經網絡技術實現機器學習的全噪聲自動編碼器
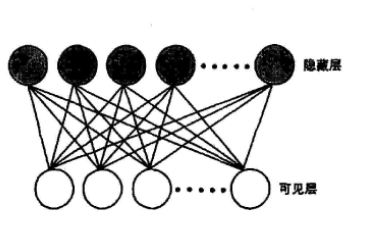
一種改進的基于半自動編碼器的協同過濾推薦算法

一種混合自動編碼器高斯混合模型MAGMM
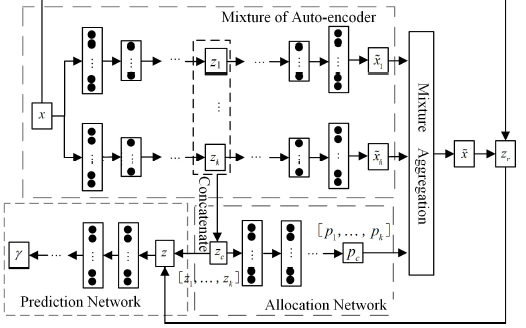
堆疊降噪自動編碼器(SDAE)
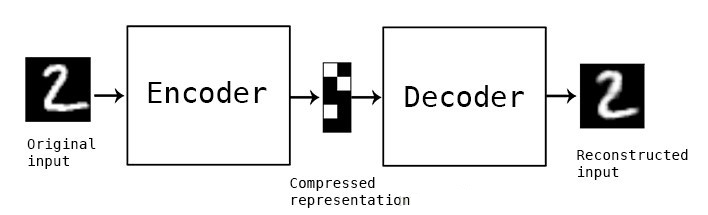




 基于權重系聯的線性自動編碼器
基于權重系聯的線性自動編碼器












評論