下面兩道題關于使用復利葉變換的, 這應該是很常見的嵌入式問題:A)系統用 adc (小于 16-bit) 采樣 50Hz 交流電流電壓, 采樣頻率800hz, 試求出電流電壓幅值以及功率和功率因數。B)上面的50hz 電壓中, 混入了另一個 55hz 的電壓, 求出這兩個電壓的幅值。這兩道題使用 16-bit, 32-bit 的整數運算, 不使用浮點運算, 可以在 mcu 上實現。C)完成一個 wav 聲音文件的變速不變調的程序。
(1)復數的基礎知識
在講解 fourier transform 前, 大家必須知道一點基本的復數知識。在復平面上的一個點 P (x, y) 用復數表示為: P = x + i y用極坐標表示為: P = r * e^(i a)這里,r = sqrt(x*x + y*) 是點 (x, y) 到原點的距離, a = arctan2(x, y) 是角度, e 是自然常數。這里引出了一個非常重要的表達式: e^(i a)= cos(a) + i sin(a)這個表達式,是利用復數完成角度變換和三角函數變換的利器。例如,把點 P 旋轉 b 角度,那么新點(x1, y1) 的角度為 a+b, 距離仍為 r. P1 = x1 + i y1 = r * e^(i (a+b)) = r*e^(i a) * e^(i b) = (x + i y) * (cos(b)+i sin(b)) = (x * cos(b) - y * sin(b)) + i ( y * cos(b) + x * sin(b)) (2)傅里葉變換的基礎知識傅里葉變換是一個積分變換, 公式就不提供了, 有興趣的同學可以直接訪問下面的連接, 以獲得更詳盡的解釋:http://zh.wikipedia.org/zh-cn/%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2(3) 離散傅里葉變換(DFT)http://zh.wikipedia.org/zh-cn/%E7%A6%BB%E6%95%A3%E5%82%85%E9%87%8C%E5%8F%B6%E5%8F%98%E6%8D%A2離散傅里葉變換的公式: X(k)= ∑ x(n) * e^(i -2*PI* n/N * k) / N這里 X(k) 是第 k 次諧波的復數;N 為周期采樣點數;x(n)為輸入,n從0 到N-1; 用偽代碼更直觀地說明: void CalculateHarmonic(Complex* X, int harmonic) { for (int i=0; i
總結一下:傅里葉變換可以很深奧, 也可以很淺顯。對于離散的傅里葉變換的公式, 只要認真的看看很容易看明白, 更何況還有代碼說明。通過理解 dft 如何計算出某一個諧波, 就可以進一步計算出所有諧波, 再想象一下, 某一個算法, 可以快速的計算出所有的諧波, 這樣, 就可以很容易的理解 fft.
(5) 問題 A 的解答在上面的代碼CalculateHarmonic(Complex* X, int harmonic)中可以看出dft 的各次諧波計算是獨立的, 不依賴其它次諧波。而且,問題 A 不需要計算2次(100hz),3次(150hz)等等諧波,這是 dft 的優點之一。首先,定義兩個復數的結構:
typedef short int16;
typedef int int32;
typedef struct SComplex
{
int16 R;
int16 I;
} Complex;
typedef struct SComplex32
{
int32 R;
int32 I;
} Complex32;
接著, 定義兩個常數以及電壓電流的結構:
#define N 16 //每周期采樣點數
#define LOG2_N 4 // log2(N)
struct UI {
ComplexU; //電壓的結果
ComplexI; //電流的結果
int16Voltage[N]; //先前的 N 個電壓
int16Current[N]; //先前的 N 個電流
Complex32 UAcc;//電壓的累加器
Complex32 IAcc; //電流的累加器
int Index;//迭代索引計數器, 8-BIT MCU 可以為 char, 如果 N < 256.
ComplexW[N];//N 點的 cos, sin 系數
} ui;
初始化,cos, sin 系數數組應該事先計算好:
void UI_Init()
{
for (int i=0; i
ui.W[i].R = (int16) (::cos( 2*3.1415927*i/N) * (1<<14) + 0.5); //應離線計算!!!
ui.W[i].I = (int16) (::sin(-2*3.1415927*i/N) * (1<<14) + 0.5);
ui.Voltage[i] = 0;
ui.Current[i] = 0;
}
ui.UAcc.R = 0; ui.UAcc.I = 0;
ui.IAcc.R = 0; ui.IAcc.I = 0;
ui.Index = 0;
}
下面的代碼不斷遞推, 可以求出電壓和電流的復數:
void UI_Calculate(int16 voltage, int16 current)
{
int16 d;
d = voltage - ui.Voltage[ui.Index];
ui.Voltage[ui.Index] = voltage;
ui.UAcc.R += (d * ui.W[ui.Index].R) >> (13 + LOG2_N - 16);
ui.UAcc.I += (d * ui.W[ui.Index].I) >> (13 + LOG2_N - 16);
ui.U.R = (int16) (ui.UAcc.R >> 16);
ui.U.I = (int16) (ui.UAcc.I >> 16);
d = current - ui.Current[ui.Index];
ui.Current[ui.Index] = current;
ui.IAcc.R += (d * ui.W[ui.Index].R) >> (13 + LOG2_N - 16);
ui.IAcc.I += (d * ui.W[ui.Index].I) >> (13 + LOG2_N - 16);
ui.I.R = (int16) (ui.IAcc.R >> 16);
ui.I.I = (int16) (ui.IAcc.I >> 16);
ui.Index = (ui.Index + 1) & (N-1);
}
上面的計算dft計算使用的是 16-bit, 32-bit 的定點運算,這里需要把電壓和電流單位化。比如系統最大電壓幅值為 Vmax = 400V,最大電流幅值 Imax = 20A, 在數字系統中統一歸一化:Q15 = 2^15 = 32768. 即 Vmax,Imax在數字系統對應Q15 = 32768. 因此,演示主程序中的: 8000 ---〉8000/Q15 * Vmax=97.66V 4000 ---〉4000/Q15 * Imax= 2.441A至于功率,很簡單, 用電壓乘以電流的軛(用 j 來代替復數i, 以免混淆): P + jQ = U*I’ = (ui.U.R + j ui.U.I) * (ui.I.R – j ui.I.I)P是有功功率, Q是無功功率;功率因數為:cos(theta) = P / sqrt(P*P +Q*Q)
visual c++下的演示主程序 :
#include "stdafx.h"
#include "Math.h"
#include "stdio.h"
#include "UI.h"
#define Magnitude(c) ((int) sqrtf(c.R*c.R + c.I*c.I))
#define PI 3.14159265f
int _tmain(int argc, _TCHAR* argv[])
{
int16 voltage, current;
Complex PQ;
UI_Init();
for (int i=0; i<1000; i++) {
voltage = (int16) (::sin(2*PI*i/N)*8000); //模擬采樣電壓
current = (int16) (::sin(2*PI*i/N + PI/3)* 4000);//模擬采樣電流
UI_Calculate(voltage, current);
}
PQ.R = (ui.U.R * ui.I.R + ui.U.I * ui.I.I) >> 15;
PQ.I = (ui.U.I * ui.I.R - ui.U.R * ui.I.I) >> 15;
printf("Voltage: %d\n",Magnitude(ui.U));
printf("Cuurent: %d\n",Magnitude(ui.I));
printf("Power Factor: %d\n", PQ.R * 1000 / Magnitude(PQ));
::getchar();
return 0;
}
結果
Voltage: 8000Cuurent: 3999Power Factor: 500
6)問題B的解答現在大家已經知道了,DFT可以單獨的計算各個諧波。這道題,同樣可以用DFT來做,當然也可以用FFT來做。50Hz與55hz相差5Hz,所以必須采用5Hz的分辨率。采樣頻率為800Hz,周期T800 = 1.25ms;5Hz周期T5 = 200 ms.因此,5hz數據窗口的長度為N = T5 / T800 = 160,這樣50Hz, 55Hz就分別是10,11次諧波。定義常數:
#define N 160
#define LOG2_N 8
計算cos, sin系數。注意(1<<(14 + LOG2_N)) / N 的作用
for (int i=0; i
ui.W[i].R = (int16) (::cos( 2*3.1415927*i/N) * (1<<(14 + LOG2_N)) / N + 0.5);
ui.W[i].I = (int16) (::sin(-2*3.1415927*i/N) * (1<<(14 + LOG2_N)) / N + 0.5);
ui.Voltage[i] = 0;
}
計算:
void UI_Calculate(int16 voltage)
{
int16 d;
int i;
d = voltage - ui.Voltage[ui.Index];
ui.Voltage[ui.Index] = voltage;
i = (ui.Index * 10) % N;
ui.U10_Acc.R += (d * ui.W[i].R) >> (13 + LOG2_N - 16);
ui.U10_Acc.I += (d * ui.W[i].I) >> (13 + LOG2_N - 16);
ui.U10.R = (int16) (ui.U10_Acc.R >> 16);
ui.U10.I = (int16) (ui.U10_Acc.I >> 16);
i = (ui.Index * 11) % N;
ui.U11_Acc.R += (d * ui.W[i].R) >> (13 + LOG2_N - 16);
ui.U11_Acc.I += (d * ui.W[i].I) >> (13 + LOG2_N - 16);
ui.U11.R = (int16) (ui.U11_Acc.R >> 16);
ui.U11.I = (int16) (ui.U11_Acc.I >> 16);
ui.Index = (ui.Index + 1) % N;
}
注意(13 + LOG2_N - 16)的作用。
演示主程序:
int _tmain(int argc, _TCHAR* argv[])
{
UI_Init();
float Hz50 = 2 * PI * 50 / 800;
float Hz55 = 2 * PI * 55 / 800;
for (int i=0; i<1000; i++) {
UI_Calculate((int16) (::sin(Hz50*i)*8000 + ::sin(Hz55*i)* 4000));
}
printf("50Hz: %d\n",Magnitude(ui.U10));
printf("55Hz: %d\n",Magnitude(ui.U11));
::getchar();
return 0;
}
結果:50Hz: 800055Hz: 4000
上面的例子有一個問題就是N=160,這對于小ram容量的mcu來說,不太合適。我們可以做一些改動。一是改變采樣頻率,二是保持采樣頻率不變,跳過幾個點,變相的改變采樣頻率。這里我們可以每采樣5次,計算一次,這樣N=160/5=32.#define N 32#define LOG2_N 5for (int i=0; i<1000; i++) {?? if ((i % 5) == 0)?? ? UI_Calculate((int16) (::sin(Hz50*i)*8000 + ::sin(Hz55*i)* 4000)); }得到了一樣的結果,而數據buffer 為 32, 可以計算出上到 15 次諧波。
介紹完 DFT, 下面輪到FFT. 我現在發現變速不變調不適合作為 FFT 的例子, 因為變速不變調涉及了很多其他的概念, 驗證程序用 matlab 做的, 雖然不長, 但是用了 matlab 里 FFT, IFFT 的命令, 所以沒有典型性。而DFT/FFT與逆變換 IDFT/IFFT 的定點 c/c++ 程序都是我自己做的, 可以更詳細的講解。FFT 容我這兩天設想一個經典的例子, 另外開一個帖子講解。
總結:傅里葉變換的實質是把一個信號通過正交分解(e^(jωt) =cos(ωt)+ j sin(ωt)), 分解成無數的正弦信號, 而這些無數的正弦信號還可以重新被合成為原來的信號。就像白光通過三棱鏡分解成光譜, 再通過三棱鏡可以被還原成白光一樣,傅里葉變換就是那個三棱鏡, 或者說三棱鏡就是一個傅里葉變換。 e^(jωt) =cos(ωt)+ j sin(ωt)可以看做鐘表的指針以的角速度ω旋轉時, 指針在縱橫兩個方向上的投影, 在橫軸上的投影就是sin(ωt). 假設兩個不同時間的鐘表疊放在一起, 你坐在其中的一個秒指針上, 你會發現另一塊表的秒指針是靜止的, 并且在你的指針上的投影是固定的。現在設想一下很多塊表的秒指針以不同的速率旋轉, 而你所乘坐的秒指針可以控制旋轉速率, 那么你會發現, 總可以使某一個秒指針看上去是靜止的, 即在你的指針上的投影是常數,與速度無關。傅里葉變換出來的是什么? 以離散的傅里葉變換DFT/FFT來說明,對N點的數據做傅里葉變換,得到了 N/2 個復數, 這每一個復數實際上代表了一個正弦波, 假設 采樣頻率為 F, 那么基本頻率為 ω0 = 2*PI*F/N這 N/2 個復數: Y[0] = x0 + j y0 :ω= 0,即 DC. Y[1] = x1 + j y1 = r1* e^(j a1): ω= ω0,代表正弦波r1* sin( ω0 * t+ a1) Y[2] = x2 + j y2 = r2* e^(j a2): ω= 2*ω0,代表正弦波r2* sin(2*ω0 * t+ a2) .... Y[k] = xk + j yk = rk* e^(j ak): ω= k*ω0,代表正弦波rk* sin(k*ω0 * t+ ak) ... Y[N/2 - 1] =所以, 這些復數的意義在于正弦波的代表, 不是一般意義上的復數。把上面的正弦波疊加在一起, 又可以得到原來的波形。
首先, 我貼出的DFT程序都是我自己寫的, 而且有匯編的版本。 大家已經看到了, c 版本完全使用了16-bit 整數乘法, 32-bit 加法以及少量的移位操作,除法(主要是 %,用于非 2的次方的 N) 可以完全避開。可以設定在每次定時中斷里采樣后計算, 由于遞推, 計算量很低(2個16bit乘法, 2個32bit 加法)。 唯一的問題是, 必須使用定點 scale 轉換以避免浮點運算, 這不如直接使用浮點直觀, 對沒有處理經驗的程序員可能是一個挑戰。雖然演示程序為了通用起見用了 PC, 但是dft 算法程序用在 avr, 51等 8-bit mcu 是完完全全沒有問題的。不要再說出單片機不能實現的胡話出來。FFT程序我也有匯編的版本,C/C++ 版本也是采用了16-bit 整數乘法, 32-bit 加法以及少量的移位操作,效率很高, 不過在8-bitmcu 上可能用不上, 因為, 數據窗口點數少了, 用 dft 更好,數據窗口點數多了, 8-bit mcu 上太慢, 不實用。 因此我就不介紹了。最后, 我貼出我用matlab做的變速不變調的算法驗證程序, 作為結束。簡單的講一講原理:下面的程序使用了短時博立葉變換(short time fourier transform),窗口函數為 hamming。1) 短時博立葉變換, 這里的片斷 segment = N/4, 數據被分割為 0 到N-1,N/4 to N+N/4-1, N/2 to N+N/2-1, 依次類推。2) 做 fft, 計算出幅度和相位。3)計算新的幅度和相位。幅度通過插植, 相位得把wt 計入:da(2: (1 + NX/2)) = (2*pi*segment) ./ (NX ./ (1: (NX/2)));4)用新的幅度和相位產生新的復數, 加窗并作 ifft 生成變速后的音頻數據。
SPEED = 2;
[in_rl, fs] = wavread('C:\windows\Media\Windows XP Startup.wav');
in = in_rl(:, 1)';
sizeOfData = length(in);
N = 2048;
segment = N/4;
window = hamming(N)';
X = zeros((1+ N/2), 1 + fix((sizeOfData - N)/segment));
c = 1;
for i = 0: segment: (sizeOfData - N)
fftx = fft(window .* in((i+1): (i+N)));
X(:, c) = fftx(1: (1+N/2))';
c = c + 1;
end;
[Xrows, Xcols] = size(X);
NX = 2 * (Xrows - 1);
Y = zeros(Xrows, round((Xcols - 1) / SPEED));
da = zeros(1, NX/2+1);
da(2: (1 + NX/2)) = (2*pi*segment) ./ (NX ./ (1: (NX/2)));
phase = angle(X(:, 1));
c = 1;
for i = 0: SPEED: (Xcols-2)
X1 = X(:, 1 + floor(i));
X2 = X(:, 2 + floor(i));
df = i - floor(i);
magnitude = (1-df) * abs(X1) + df * (abs(X2));
dangle = angle(X2) - angle(X1);
dangle = dangle - da' - 2 * pi * round(dangle/(2*pi));
Y(:, c) = magnitude .* exp(j * phase);
phase = phase + da' + dangle;
c = c + 1;
end
[Yrows, Ycols] = size(Y);
out = zeros(1, N + (Ycols - 1) * segment );
c = 1;
for i = 0: segment: (segment * (Ycols-1))
Yc = Y(:, c)';
Ynew = [Yc, conj(Yc((N/2): -1: 2))];
out((i+1): (i+N)) = out((i+1)i+N)) + real(ifft(Ynew)) .* window;
c = c + 1;
end;
wavplay(out, fs);
-
嵌入式
+關注
關注
5085文章
19138瀏覽量
305779 -
代碼
+關注
關注
30文章
4793瀏覽量
68700
原文標題:舉幾個例子弄清復立葉變換的應用
文章出處:【微信號:WW_CGQJS,微信公眾號:傳感器技術】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
關于圖像的頻域濾波后的傅里葉逆變換,大家進來看看。...
DSP教程--快速富利葉變換
臺灣立葉高速沖床
傅里葉級數和傅里葉變換的關系
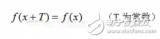




 復立葉變換你知道是什么嗎?
復立葉變換你知道是什么嗎?










評論