▌引子
最近開始拾起來看一些 NLP 相關(guān)的東西,特別是深度學(xué)習(xí)在 NLP 上的應(yīng)用,發(fā)現(xiàn)采樣方法在很多模型中應(yīng)用得很多,因為訓(xùn)練的時候如果預(yù)測目標(biāo)是一個詞,直接的 softmax 計算量會根據(jù)單詞數(shù)量的增長而增長。恰好想到最開始深度學(xué)習(xí)在 DBN 的時候采樣也發(fā)揮了關(guān)鍵的作用,而自己對采樣相關(guān)的方法了解不算太多,所以去學(xué)習(xí)記錄一下,經(jīng)典的統(tǒng)計的方法確實巧妙,看起來非常有收獲。
本篇文章先主要介紹一下經(jīng)典的采樣方法如 Inverse Sampling、Rejective Sampling 以及 Importance Sampling 和它在 NLP 上的應(yīng)用,后面還會有一篇來嘗試介紹 MCMC 這一組狂炫酷拽的算法。才疏學(xué)淺,行文若有誤望指正。
▌Why Sampling
采樣是生活和機器學(xué)習(xí)算法中都會經(jīng)常用到的技術(shù),一般來說采樣的目的是評估一個函數(shù)在某個分布上的期望值,也就是
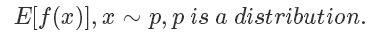
比如我們都學(xué)過的拋硬幣,期望它的結(jié)果是符合一個伯努利分布的,定義正面的概率為 p ,反面概率為 1-p 。最簡單地使 f(x)=x,在現(xiàn)實中我們就會通過不斷地進行拋硬幣這個動作,來評估這個概率p。
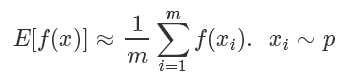
這個方法也叫做蒙特卡洛法(Monte Carlo Method),常用于計算一些非常復(fù)雜無法直接求解的函數(shù)期望。
對于拋硬幣這個例子來說:
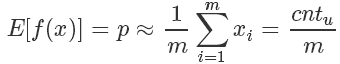
其期望就是拋到正面的計數(shù)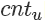 除以總次數(shù) m。?
除以總次數(shù) m。?
而我們拋硬幣的這個過程其實就是采樣,如果要用程序模擬上面這個過程也很簡單,因為伯努利分布的樣本很容易生成:
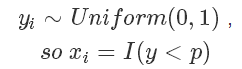
而在計算機中的隨機函數(shù)一般就是生成 0 到 1 的均勻分布隨機數(shù)。
▌Sampling Method
可以看到蒙特卡洛法其實就是按一定的概率分布中獲取大量樣本,用于計算函數(shù)在樣本的概率分布上的期望。其中最關(guān)鍵的一個步驟就是如何按照指定的概率分布 p 進行樣本采樣,拋硬幣這個 case 里伯努利分布是一個離散的概率分布,它的概率分布一般用概率質(zhì)量函數(shù)(pmf)表示,相對來說比較簡單,而對于連續(xù)概率分布我們需要考慮它的概率密度函數(shù)(pdf):
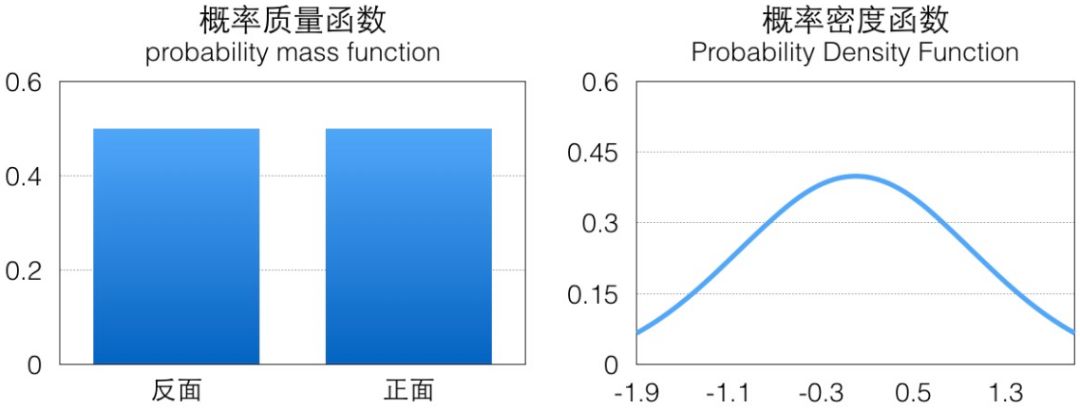
比如上圖示例分別是標(biāo)準(zhǔn)正態(tài)分布概率密度函數(shù),它們的面積都是 1(這是概率的定義),如果我們可以按照相應(yīng)概率分布生成很多樣本,那這些樣本繪制出來的直方圖應(yīng)該跟概率密度函數(shù)是一致的。
而在實際的問題中,p 的概率密度函數(shù)可能會比較復(fù)雜,我們由淺入深,看看如何采樣方法如何獲得服從指定概率分布的樣本。
▌Inverse Sampling
對于一些特殊的概率分布函數(shù),比如指數(shù)分布:
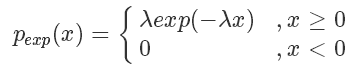
我們可以定義它的概率累積函數(shù)(Cumulative distribution function),也就是(ps.這個’F’和前面的’f’函數(shù)并沒有關(guān)系)
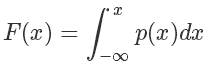
從圖像上看就是概率密度函數(shù)小于 x 部分的面積。這個函數(shù)在 x≥0 的部分是一個單調(diào)遞增的函數(shù)(在定義域上單調(diào)非減),定義域和值域是[0,+∞)→[0,1),畫出來大概是這樣子的一個函數(shù),在 p(x) 大的地方它增長快(梯度大),反之亦然:
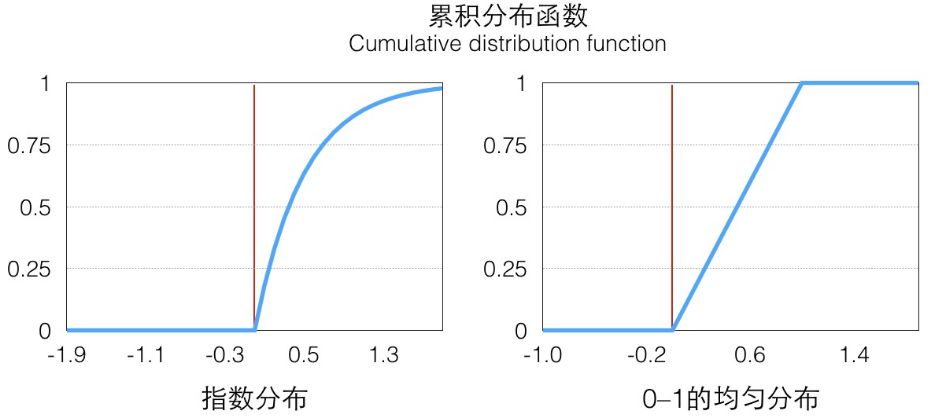
因為它是唯一映射的(在>0的部分,接下來我們只考慮這一部分),所以它的反函數(shù)可以表示為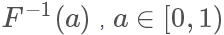 ,值域為[0,+∞)
,值域為[0,+∞)
因為F單調(diào)遞增,所以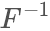 也是單調(diào)遞增的:?
也是單調(diào)遞增的:?
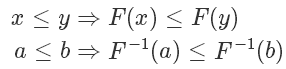
利用反函數(shù)的定義,我們有:
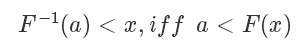
我們定義一下 [0,1] 均勻分布的 CDF,這個很好理解:
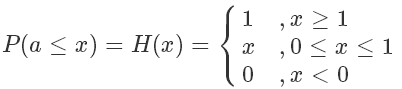
所以
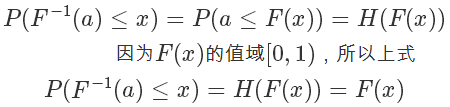
根據(jù) F(x) 的定義,它是 exp 分布的概率累積函數(shù),所以上面這個公式的意思是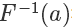 符合 exp 分布,我們通過 F 的反函數(shù)將一個 0 到 1 均勻分布的隨機數(shù)轉(zhuǎn)換成了符合 exp 分布的隨機數(shù),注意,以上推導(dǎo)對于 cdf 可逆的分布都是一樣的,對于 exp 來說,它的反函數(shù)的形式是:?
符合 exp 分布,我們通過 F 的反函數(shù)將一個 0 到 1 均勻分布的隨機數(shù)轉(zhuǎn)換成了符合 exp 分布的隨機數(shù),注意,以上推導(dǎo)對于 cdf 可逆的分布都是一樣的,對于 exp 來說,它的反函數(shù)的形式是:?
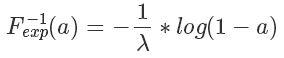
具體的映射關(guān)系可以看下圖(a),我們從 y 軸 0-1 的均勻分布樣本(綠色)映射得到了服從指數(shù)分布的樣本(紅色)。
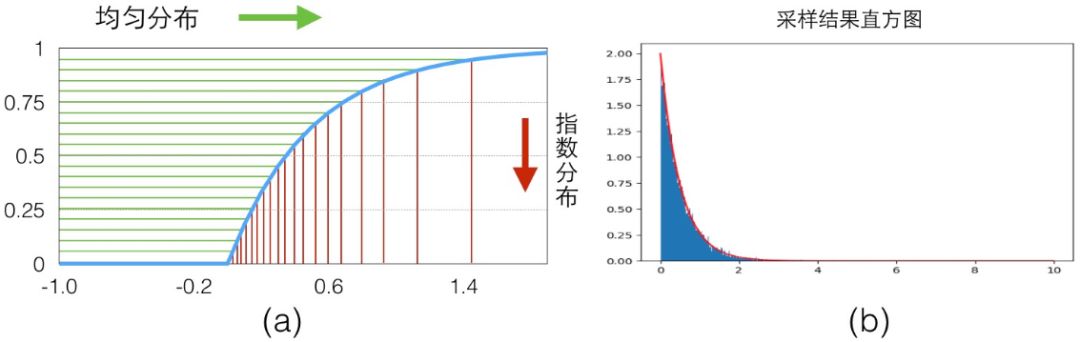
我們寫一點代碼來看看效果,最后繪制出來的直方圖可以看出來就是 exp 分布的圖,見上圖(b),可以看到隨著采樣數(shù)量的變多,概率直方圖和真實的 CDF 就越接近:
defsampleExp(Lambda=2,maxCnt=50000):ys=[]standardXaxis=[]standardExp=[]foriinrange(maxCnt):u=np.random.random()y=-1/Lambda*np.log(1-u)#F-1(X)ys.append(y)foriinrange(1000):t=Lambda*np.exp(-Lambda*i/100)standardXaxis.append(i/100)standardExp.append(t)plt.plot(standardXaxis,standardExp,'r')plt.hist(ys,1000,normed=True)plt.show()
▌Rejective Sampling
我們在學(xué)習(xí)隨機模擬的時候通常會講到用采樣的方法來計算 π 值,也就是在一個 1×1 的范圍內(nèi)隨機采樣一個點,如果它到原點的距離小于 1,則說明它在1/4 圓內(nèi),則接受它,最后通過接受的占比來計算 1/4 圓形的面積,從而根據(jù)公式反算出預(yù)估的ππ值,隨著采樣點的增多,最后的結(jié)果 會越精準(zhǔn)。?
會越精準(zhǔn)。?

上面這個例子里說明一個問題,我們想求一個空間里均勻分布的集合面積,可以嘗試在更大范圍內(nèi)按照均勻分布隨機采樣,如果采樣點在集合中,則接受,否則拒絕。最后的接受概率就是集合在‘更大范圍’的面積占比。
當(dāng)我們重新回過頭來看想要 sample 出來的樣本服從某一個分布 p,其實就是希望樣本在其概率密度函數(shù)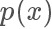 高的地方出現(xiàn)得更多,所以一個直覺的想法,我們從均勻分布隨機生成一個樣本?
高的地方出現(xiàn)得更多,所以一個直覺的想法,我們從均勻分布隨機生成一個樣本?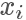 ,按照一個正比于?
,按照一個正比于?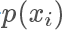 的概率接受這個樣本,也就是說雖然是從均勻分布隨機采樣,但留下的樣本更有可能是?
的概率接受這個樣本,也就是說雖然是從均勻分布隨機采樣,但留下的樣本更有可能是?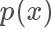 高的樣本。
高的樣本。
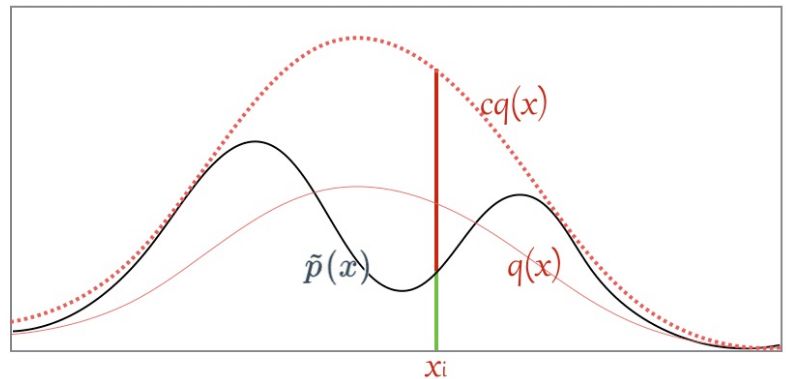
這樣的思路很自然,但是否是對的呢。其實這就是 Rejective Sampling 的基本思想,我們先看一個很 intuitive 的圖
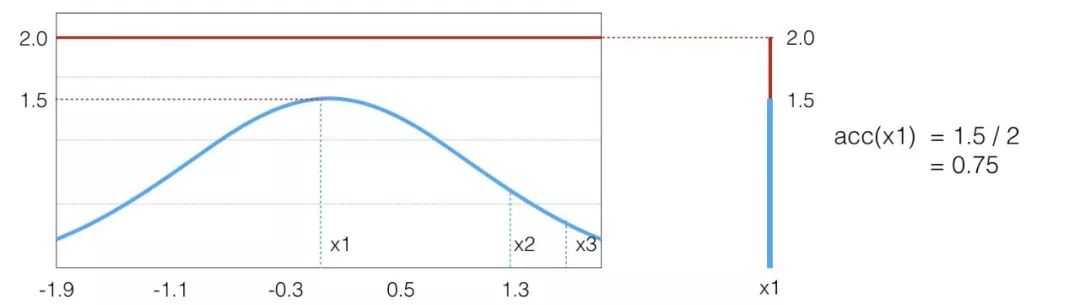
假設(shè)目標(biāo)分布的 pdf 最高點是 1.5,有三個點它們的 pdf 值分別是
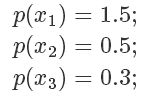
因為我們從 x 軸上是按均勻分布隨機采樣的,所以采樣到三個點的概率都一樣,也就是
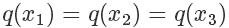
接下來需要決定每個點的接受概率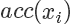 ,它應(yīng)該正比于?
,它應(yīng)該正比于?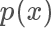 ,當(dāng)然因為是概率值也需要小于等于 1.?
,當(dāng)然因為是概率值也需要小于等于 1.?
我們可以畫一根 y=2 的直線,因為整個概率密度函數(shù)都在這根直線下,我們設(shè)定
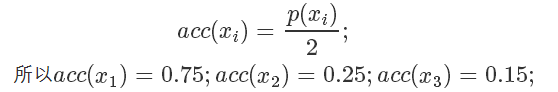
我們要做的就是生成一個 0-1的隨機數(shù)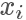 ,如果它小于接受概率?
,如果它小于接受概率?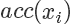 ,則留下這個樣本。因為?
,則留下這個樣本。因為?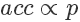 ,所以可以看到因為?
,所以可以看到因為?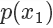 是?
是?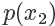 的3倍,所以?
的3倍,所以?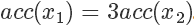 。同樣采集 100 次,最后留下來的樣本數(shù)期望也是 3 倍。這根本就是概率分布的定義!
。同樣采集 100 次,最后留下來的樣本數(shù)期望也是 3 倍。這根本就是概率分布的定義!
我們將這個過程更加形式化一點,我們我們又需要采樣的概率密度函數(shù)
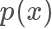 ,但實際情況我們很有可能只能計算出?
,但實際情況我們很有可能只能計算出?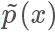 ,有
,有
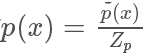
我們需要找一個可以很方便進行采樣的分布函數(shù)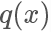 并使?
并使?
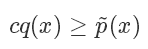
其中 c 是需要選擇的一個常數(shù)。然后我們從 q 分布中隨機采樣一個樣本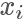 ,并以?
,并以?
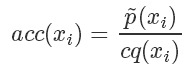
的概率決定是否接受這個樣本。重復(fù)這個過程就是「拒絕采樣」算法了。
在上面的例子我們選擇的 q 分布是均勻分布,所以從圖像上看其 pdf 是直線,但實際上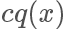 和?
和?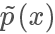 越接近,采樣效率越高,因為其接受概率也越高:?
越接近,采樣效率越高,因為其接受概率也越高:?
▌Importance Sampling
上面描述了兩種從另一個分布獲取指定分布的采樣樣本的算法,對于1.在實際工作中,一般來說我們需要 sample 的分布都及其復(fù)雜,不太可能求解出它的反函數(shù),但 p(x) 的值也許還是可以計算的。對于2.找到一個合適的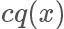
那我們回過頭來看我們sample的目的:其實是想求得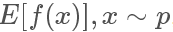 ,也就是?
,也就是?
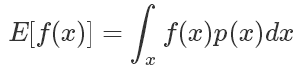
如果符合 p(x) 分布的樣本不太好生成,我們可以引入另一個分布 q(x),可以很方便地生成樣本。使得
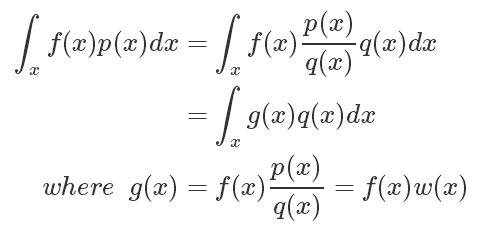
我們將問題轉(zhuǎn)化為了求 g(x) 在 q(x) 分布下的期望!!!
我們稱其中的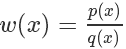 叫做?Importance Weight.
叫做?Importance Weight.
▌Importance Sample 解決的問題
首先當(dāng)然是我們本來沒辦法 sample from p,這個是我們看到的,IS 將之轉(zhuǎn)化為了從 q 分布進行采樣;同時 IS 有時候還可以改進原來的 sample,比如說:
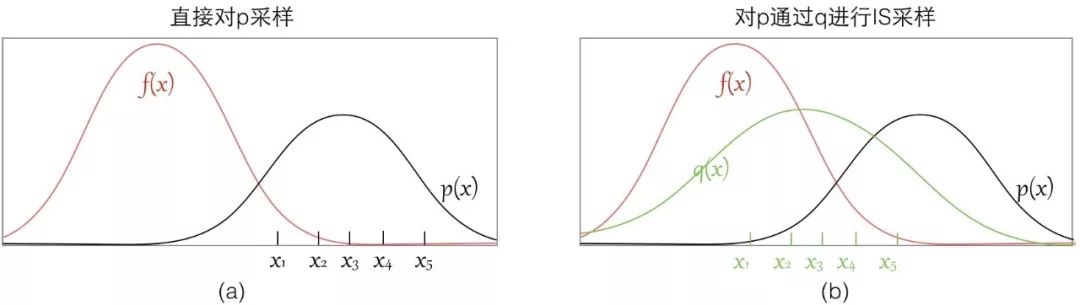
可以看到如果我們直接從 p 進行采樣,而實際上這些樣本對應(yīng)的 f(x) 都很小,采樣數(shù)量有限的情況下很有可能都無法獲得 f(x) 值較大的樣本,這樣評估出來的期望偏差會較大;
而如果我們找到一個 q 分布,使得它能在 f(x)*p(x) 較大的地方采集到樣本,則能更好地逼近 [Ef(x)],因為有 Importance Weight 控制其比重,所以也不會導(dǎo)致結(jié)果出現(xiàn)過大偏差。
所以選擇一個好的p也能幫助你sample出來的效率更高,要使得 f(x)p(x)較大的地方能被 sample出來。
▌無法直接求得p(x)的情況
上面我們假設(shè) g(x) 和 q(x) 都可以比較方便地計算,但有些時候我們這個其實是很困難的,更常見的情況市我們能夠比較方便地計算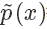 和?
和?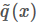
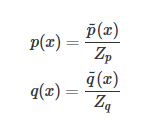
其中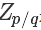 是一個標(biāo)準(zhǔn)化項(常數(shù)),使得?
是一個標(biāo)準(zhǔn)化項(常數(shù)),使得?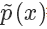 或者?
或者?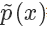 等比例變化為一個概率分布,你可以理解為 softmax 里面那個除數(shù)。也就是說?
等比例變化為一個概率分布,你可以理解為 softmax 里面那個除數(shù)。也就是說?
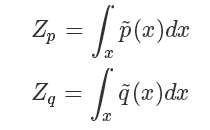
這種情況下我們的 importance sampling 是否還能應(yīng)用呢?
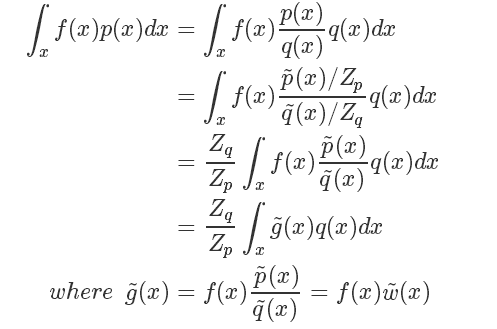
而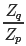 我們直接計算并不太好計算,而它的倒數(shù):?
我們直接計算并不太好計算,而它的倒數(shù):?
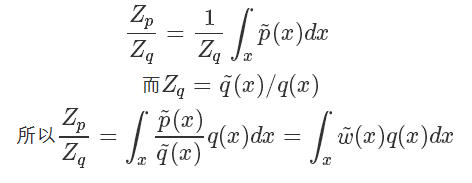
因為我們家設(shè)能很方便地從 q 采樣,所以上式其實又被轉(zhuǎn)化成了一個蒙特卡洛可解的問題,也就是
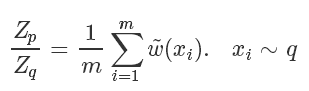
最終最終,原來的蒙特卡洛問題變成了:
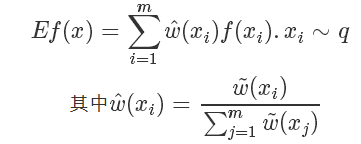
所以我們完全不用知道 q(x) 確切的計算值,就可以近似地從中得到在 q 分布下 f(x) 的取值!!amazing!
▌Importance Sampling在深度學(xué)習(xí)里面的應(yīng)用
在深度學(xué)習(xí)特別是NLP的Language Model中,訓(xùn)練的時候最后一層往往會使用 softmax 函數(shù)并計算相應(yīng)的梯度。
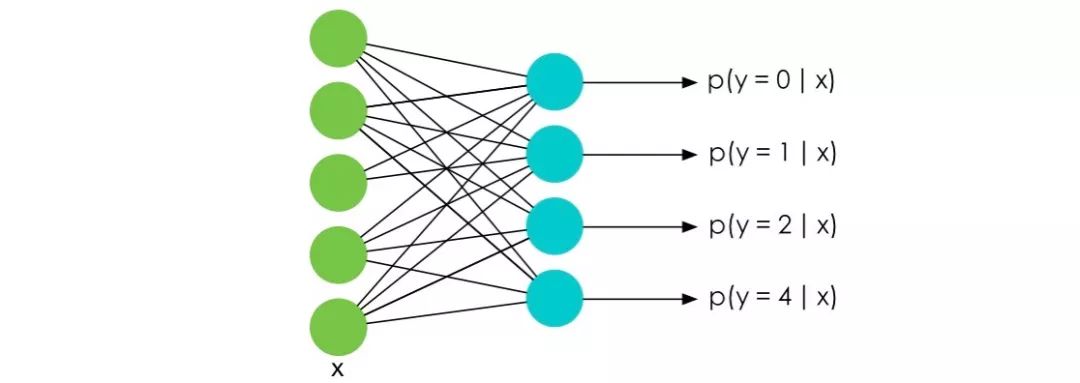
而我們知道 softmax 函數(shù)的表達式是:
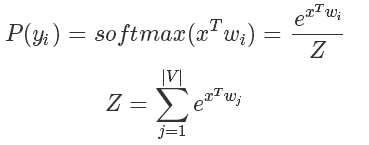
要知道在 LM 中 m 的大小是詞匯的數(shù)量決定的,在一些巨大的模型里可能有幾十萬個詞,也就意味著計算Z的代價十分巨大。
而我們在訓(xùn)練的時候無非是想對 softmax 的結(jié)果進行求導(dǎo),也就是說
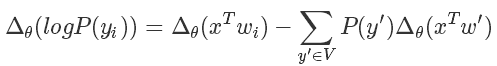
后面那一塊,我們好像看到了熟悉的東西,沒錯這個形式就是為采樣量身定做似的。
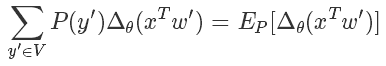
經(jīng)典的蒙特卡洛方法就可以派上用途了,與其枚舉所有的詞,我們只需要從 V 里 sample 出一些樣本詞,就可以近似地逼近結(jié)果了。
同時直接從 P 中 sample 也不可取的,而且計算 P是非常耗時的事情(因為需要計算Z),我們一般只能計算 ,而且直接從 P 中 sample 也不可取,所以我們選擇另一個分布 Q 進行 Importance Sample 即可。
,而且直接從 P 中 sample 也不可取,所以我們選擇另一個分布 Q 進行 Importance Sample 即可。
一般來說可能選擇的 Q 分布是簡單一些的 n-gramn 模型。下面是論文中的算法偽代碼,基本上是比較標(biāo)準(zhǔn)的流程(論文圖片的符號和上面的描述稍有出入,理解一下過程即可):

References
【1】mathematicalmonk’s machine learning course on y2b. machine learing
【2】Pattern Recognition And Machine Learning
【3】Adaptive Importance Sampling to Accelerate Trainingof a Neural Probabilistic Language Model.Yoshua Bengio and Jean-Sébastien Senécal.
?
采樣方法 2
▌引子
在上面我們講到了拒絕采樣、重要性采樣一系列的蒙特卡洛采樣方法,但這些方法在高維空間時都會遇到一些問題,因為很難找到非常合適的可采樣Q分布,同時保證采樣效率以及精準(zhǔn)度。
本文將會介紹采樣方法中最重要的一族算法,MCMC(Markov Chain Monte Carlo),在之前我們的蒙特卡洛模擬都是按照如下公式進行的:
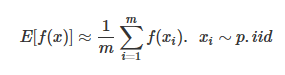
我們的x都是獨立采樣出來的,而在MCMC中,它變成了
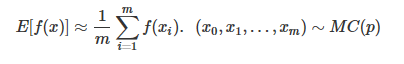
其中的MC(p)就是我們本文的主角之一,馬爾可夫過程(Markov Process)生成的馬爾可夫鏈(Markov Chain)。
▌Markov Chain(馬爾可夫鏈)
在序列的算法(一·a)馬爾可夫模型中(https://blog.csdn.net/dark_scope/article/details/61417336)我們就說到了馬爾可夫模型的馬爾可夫鏈,簡單來說就是滿足馬爾可夫假設(shè)
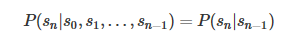
的狀態(tài)序列,由馬爾可夫過程(Markov Process)生成。
一個馬爾可夫過程由兩部分組成,一是狀態(tài)集合Ω,二是轉(zhuǎn)移概率矩陣T。
其流程是:選擇一個初始的狀態(tài)分布π0,然后進行狀態(tài)的轉(zhuǎn)移:
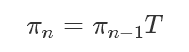
得到的π0,π1,π2 ...πn 狀態(tài)分布序列。
注意:我們在這里講的理論和推導(dǎo)都是基于離散變量的,但其實是可以直接推廣到連續(xù)變量。
馬爾可夫鏈在很多場景都有應(yīng)用,比如大名鼎鼎的 pagerank 算法,都用到了類似的轉(zhuǎn)移過程;
馬爾可夫鏈在某種特定情況下,有一個奇妙的性質(zhì):在某種條件下,當(dāng)你從一個分布π0開始進行概率轉(zhuǎn)移,無論你一開始π0 的選擇是什么,最終會收斂到一個固定的分布π,叫做穩(wěn)態(tài)(steady-state)。
穩(wěn)態(tài)滿足條件:
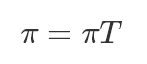
這里可以參考《LDA數(shù)學(xué)八卦0.4.2》的例子,非常生動地描述了社會階層轉(zhuǎn)化的一個例子,也對MCMC作了非常好的講解
書歸正傳,回到我們采樣的場景,我們知道,采樣的難點就在于概率密度函數(shù)過于復(fù)雜而無法進行有效采樣,如果我們可以設(shè)計一個馬爾可夫過程,使得它最終收斂的分布是我們想要采樣的概率分布,不就可以解決我們的問題了么。
前面提到了在某種特定情況下,這就是所有MCMC算法的理論基礎(chǔ)ErgodicTheorem:
如果一個離散馬爾可夫鏈(x0,x1...xm)是一個與時間無關(guān)的 Irreducible 的離散,并且有一個穩(wěn)態(tài)分布π,則:

它需要滿足的條件有這樣幾個,我們直接列在這里,不作證明:????????????????
1.Time homogeneous: 狀態(tài)轉(zhuǎn)移與時間無關(guān),這個很好理解。2.Stationary Distribution: 最終是會收斂到穩(wěn)定狀態(tài)的。3.Irreducible: 任意兩個狀態(tài)之間都是可以互相到達的。4.Aperiodic:馬爾可夫序列是非周期的,我們所見的絕大多數(shù)序列都是非周期的。
雖然這里要求是離散的馬爾可夫鏈,但實際上對于連續(xù)的場景也是適用的,只是轉(zhuǎn)移概率矩陣變成了轉(zhuǎn)移概率函數(shù)。
▌MCMC
在上面馬爾可夫鏈中我們的所說的狀態(tài)都是某個可選的變量值,比如社會等級上、中、下,而在采樣的場景中,特別是多元概率分布,并不是量從某個維度轉(zhuǎn)移到另一個維度,比如一個二元分布,二維平面上的每一個點都是一個狀態(tài),所有狀態(tài)的概率和為 1! 這里比較容易產(chǎn)生混淆,一定小心。
在這里我們再介紹一個概念:
Detail balance:一個馬爾可夫過程是細(xì)致平穩(wěn)的,即對任意 a,b 兩個狀態(tài):
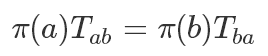
細(xì)致平穩(wěn)條件也可以推導(dǎo)出一個非周期的馬爾可夫鏈?zhǔn)瞧椒€(wěn)的,因為每次轉(zhuǎn)移狀態(tài)i從狀態(tài)j獲得的量與 j 從 i 獲得的量是一樣的,那毫無疑問最后πT=π.
所以我們的目標(biāo)就是需要構(gòu)造這樣一個馬爾可夫鏈,使得它最后能夠收斂到我們期望的分布π,而我們的狀態(tài)集合其實是固定的,所以最終目標(biāo)就是構(gòu)造一個合適的 T,就大功告成了。
一般來說我們有:
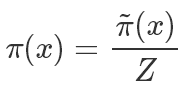
其中Z是歸一化參數(shù)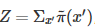 ,因為我們通常能夠很方便地計算分子
,因為我們通常能夠很方便地計算分子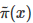 ,但是分母的計算因為要枚舉所有的狀態(tài)所以過于復(fù)雜而無法計算。我們希望最終采樣出來的樣本符合?π 分布。
,但是分母的計算因為要枚舉所有的狀態(tài)所以過于復(fù)雜而無法計算。我們希望最終采樣出來的樣本符合?π 分布。
▌Metropolis
原理描述
Metropolis 算法算是 MCMC 的開山鼻祖了,它這里假設(shè)我們已經(jīng)有了一個狀態(tài)轉(zhuǎn)移概率函數(shù)T來表示轉(zhuǎn)移概率,T(a,b) 表示從 a 轉(zhuǎn)移到 b 的概率(這里T的選擇我們稍后再說),顯然通常情況下一個T是不滿足細(xì)致平穩(wěn)條件的:
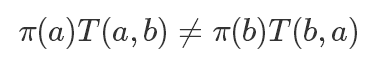
所以我們需要進行一些改造,加入一項Q使得等式成立:
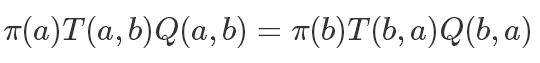
基于對稱的原則,我們直接讓
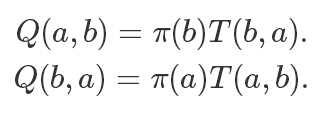
所以我們改造后的滿足細(xì)致平穩(wěn)條件的轉(zhuǎn)移矩陣就是:
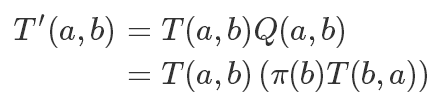
在 Metropolis 算法中,這個加入的這個 Q 項是此次轉(zhuǎn)移的接受概率,是不是和拒絕采樣有點神似。

但這里還有一個問題,我們的接受概率 Q 可能會非常小,而且其中還需要精確計算出π(x′),這個我們之前提到了是非常困難的,再回到我們的細(xì)致平穩(wěn)條件:
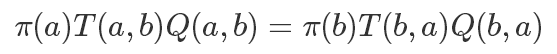
如果兩邊同時乘以一個數(shù)值,它也是成立的,比如
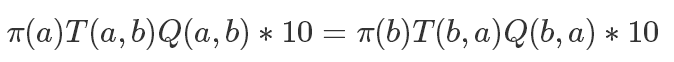
所以我們可以同步放大Q(a,b)和Q(b,a),使得其中最大的一個值為1,也就是說:
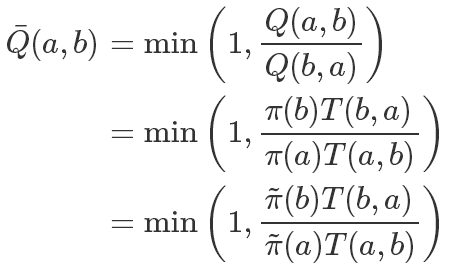
這樣在提高接受率的同時,因為除式的存在我們還可以約掉難以計算的 Z。

代碼實驗
我們之前提到狀態(tài)轉(zhuǎn)移函數(shù)T的選擇,可以看到如果我們選擇一個對稱的轉(zhuǎn)移函數(shù),即T(a,b)=T(b,a),上面的接受概率還可以簡化為
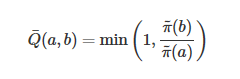
這也是一般 Metropolis 算法中采用的方法,T使用一個均勻分布即可,所有狀態(tài)之間的轉(zhuǎn)移概率都相同。
實驗中我們使用一個二元高斯分布來進行采樣模擬
其概率密度函數(shù)這樣計算的,x是一個二維坐標(biāo):
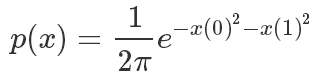
defget_p(x):#模擬pi函數(shù)return1/(2*PI)*np.exp(-x[0]**2-x[1]**2)defget_tilde_p(x):#模擬不知道怎么計算Z的PI,20這個值對于外部采樣算法來說是未知的,對外只暴露這個函數(shù)結(jié)果returnget_p(x)*20
每輪采樣的函數(shù):
defdomain_random():#計算定義域一個隨機值returnnp.random.random()*3.8-1.9defmetropolis(x):new_x=(domain_random(),domain_random())#新狀態(tài)#計算接收概率acc=min(1,get_tilde_p((new_x[0],new_x[1]))/get_tilde_p((x[0],x[1])))#使用一個隨機數(shù)判斷是否接受u=np.random.random()ifu
然后就可以完整地跑一個實驗了:
deftestMetropolis(counts=100,drawPath=False):plotContour()#可視化#主要邏輯x=(domain_random(),domain_random())#x0xs=[x]#采樣狀態(tài)序列foriinrange(counts):xs.append(x)x=metropolis(x)#采樣并判斷是否接受#在各個狀態(tài)之間繪制跳轉(zhuǎn)的線條幫助可視化ifdrawPath:plt.plot(map(lambdax:x[0],xs),map(lambdax:x[1],xs),'k-',linewidth=0.5)##繪制采樣的點plt.scatter(map(lambdax:x[0],xs),map(lambdax:x[1],xs),c='g',marker='.')plt.show()pass
可以看到采樣結(jié)果并沒有想象的那么密集,因為雖然我們提高了接受率,但還是會拒絕掉很多點,所以即使采樣了5000次,繪制的點也沒有密布整個畫面。
▌Gibbs Sampling
算法分析
通過分析 Metropolis 的采樣軌跡,我們發(fā)現(xiàn)前后兩個狀態(tài)之間并沒有特別的聯(lián)系,新的狀態(tài)都是從 T 采樣出來的,而因為原始的分布很難計算,所以我們選擇的T是均勻分布,因此必須以一個概率進行拒絕,才能保證最后收斂到我們期望的分布。
如果我們限定新的狀態(tài)只改變原狀態(tài)的其中一個維度,即
只改變了其中第 j 個維度,則有
其中
結(jié)論很清晰:這樣一個轉(zhuǎn)移概率函數(shù)T是滿足細(xì)致平穩(wěn)條件的,而且和Metropolis里面不同:它不是對稱的。
我們能夠以 1 為概率接受它的轉(zhuǎn)移結(jié)果。
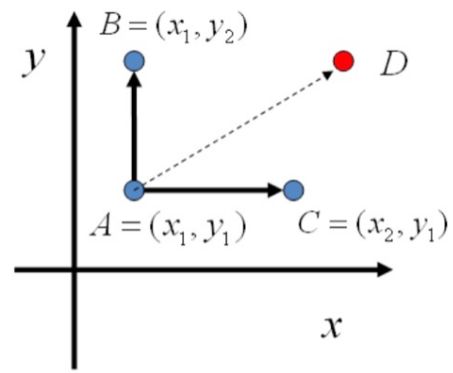
以一個二元分布為例,在平面上:
A 只能跳轉(zhuǎn)到位于統(tǒng)一條坐標(biāo)線上的 B,C 兩個點,對于 D,它無法一次轉(zhuǎn)移到達,但是可以通過兩次變換到達,仍然滿足Irreducible的條件。
這樣構(gòu)造出我們需要的轉(zhuǎn)移概率函數(shù)T之后,就直接得到我們的 Gibbs 采樣算法了:
代碼實驗
想必大家發(fā)現(xiàn)了,如果要寫代碼,我們必須要知道如何從
在我們之前實驗的場景(二元正態(tài)分布),確實也能精確地寫出這個概率分布的概率密度函數(shù)(也是一個正態(tài)分布)。
但退一步想,現(xiàn)在我們只關(guān)心一元的采樣了,所以其實是有很多方法可以用到的,比如拒絕采樣等等。
而最簡單的,直接在這一維度上隨機采幾個點,然后按照它們的概率密度函數(shù)值為權(quán)重選擇其中一個點作為采樣結(jié)果即可。
代碼里這樣做的目的主要是為了讓代碼足夠簡單,只依賴一個均勻分布的隨機數(shù)生成器。
defpartialSampler(x,dim):xes=[]fortinrange(10):#隨機選擇10個點xes.append(domain_random())tilde_ps=[]fortinrange(10):#計算這10個點的未歸一化的概率密度值tmpx=x[:]tmpx[dim]=xes[t]tilde_ps.append(get_tilde_p(tmpx))#在這10個點上進行歸一化操作,然后按照概率進行選擇。norm_tilde_ps=np.asarray(tilde_ps)/sum(tilde_ps)u=np.random.random()sums=0.0fortinrange(10):sums+=norm_tilde_ps[t]ifsums>=u:returnxes[t]
主程序的結(jié)構(gòu)基本上和之前是一樣的,
defgibbs(x):rst=np.asarray(x)[:]path=[(x[0],x[1])]fordiminrange(2):#維度輪詢,這里加入隨機也是可以的。new_value=partialSampler(rst,dim)rst[dim]=new_valuepath.append([rst[0],rst[1]])#這里最終只畫出一輪輪詢之后的點,但會把路徑都畫出來returnrst,pathdeftestGibbs(counts=100,drawPath=False):plotContour()x=(domain_random(),domain_random())xs=[x]paths=[x]foriinrange(counts):xs.append([x[0],x[1]])x,path=gibbs(x)paths.extend(path)#存儲路徑ifdrawPath:plt.plot(map(lambdax:x[0],paths),map(lambdax:x[1],paths),'k-',linewidth=0.5)plt.scatter(map(lambdax:x[0],xs),map(lambdax:x[1],xs),c='g',marker='.')plt.show()
采樣的結(jié)果:
??????????????
其轉(zhuǎn)移的路徑看到都是與坐標(biāo)軸平行的直線,并且可以看到采樣 5000 詞的時候跟 Metropolis 相比密集了很多,因為它沒有拒絕掉的點。
▌后注
本文我們講述了MCMC里面兩個最常見的算法Metropolis和Gibbs Sampling,以及它們各自的實現(xiàn)
從采樣路徑來看:
Metropolis 是完全隨機的,以一個概率進行拒絕;
而 Gibbs Sampling 則是在某個維度上進行轉(zhuǎn)移。
如果我們?nèi)匀幌M詈笫褂锚毩⑼植嫉臄?shù)據(jù)進行蒙特卡洛模擬,只需要進行多次 MCMC,然后拿每個 MCMC 的第 n 個狀態(tài)作為一個樣本使用即可。
完整的代碼見鏈接:
https://github.com/justdark/dml/blob/master/dml/tool/mcmc.py
因為從頭到尾影響分布的只有g(shù)et_p()函數(shù),所以如果我們想對其他分布進行實驗,只需要改變這個函數(shù)的定義就好了,比如說我們對一個相關(guān)系數(shù)為0.5 的二元正態(tài)分布,只需要修改 get_p() 函數(shù):
defget_p(x):return1/(2*PI*math.sqrt(1-0.25))*np.exp(-1/(2*(1-0.25))*(x[0]**2-x[0]*x[1]+x[1]**2))
就可以得到相應(yīng)的采樣結(jié)果:
而且因為這里并不要求p是一個歸一化后的分布,可以嘗試任何>0的函數(shù),比如
defget_p(x):returnnp.sin(x[0]**2+x[1]**2)+1
也可以得到采樣結(jié)果:
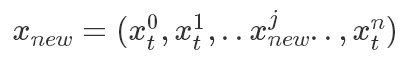
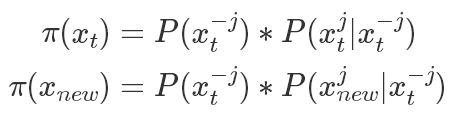
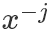 表示除了第j元其他的變量。?所以有(以
表示除了第j元其他的變量。?所以有(以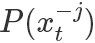 為橋梁作轉(zhuǎn)換很好得到):?
為橋梁作轉(zhuǎn)換很好得到):?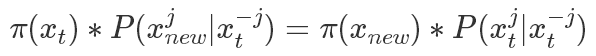


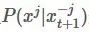 進行采樣,這是一個后驗的概率分布,在很多應(yīng)用中是能夠定義出函數(shù)表達的。
進行采樣,這是一個后驗的概率分布,在很多應(yīng)用中是能夠定義出函數(shù)表達的。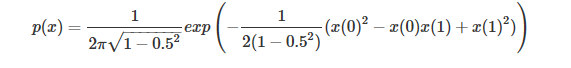
-
函數(shù)
+關(guān)注
關(guān)注
3文章
4331瀏覽量
62622 -
采樣
+關(guān)注
關(guān)注
1文章
121瀏覽量
25568 -
機器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8418瀏覽量
132646
原文標(biāo)題:一文了解采樣方法
文章出處:【微信號:rgznai100,微信公眾號:rgznai100】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
傳統(tǒng)的模擬電壓采樣保持電路方案

STM32F中AD采樣的方法有哪些
經(jīng)典的軟件濾波方法
用于圖像分類的有偏特征采樣方法
空間曲線基于內(nèi)在幾何量的均勻采樣方法

隨機采樣方法拒絕采樣思想





 經(jīng)典的采樣方法有哪些?
經(jīng)典的采樣方法有哪些?











評論