編者按:DataScience+作者Anish Singh Walia概覽了常用的神經網絡優化算法。
你是否曾經思考過該為自己的神經網絡模型使用什么樣的優化算法?我們應該使用梯度下降還是隨機梯度下降還是Adam?
什么是優化算法?
優化算法幫助我們最小化(或最大化)一個目標函數(誤差函數的另一個名字)E(x),該函數不過是一個取決于模型的內部可學習參數的數學函數,內部可學習參數用來根據一組輸入(X)計算預測目標值(Y)。例如,神經網絡的權重(W)和偏置(b)被我們稱為神經網絡的內部可學習參數,這些參數用于計算輸出值,并在優化方案的方向上學習和更新,即在網絡訓練過程中最小化損失。
模型的內部參數在訓練網絡產生精確結果的效果和效率方面起著極為重要的作用,它們影響我們模型的學習過程和模型的輸出。這正是我們使用多種優化策略和算法來更新、計算這些模型參數的恰當的最優值的原因。
優化算法的類型
優化算法可分為兩大類:
一階優化算法(First Order Optimization Algorithms)
這些算法基于損失函數在參數上的梯度值,最小化或最大化損失函數E(x)。使用最廣泛的一階優化算法是梯度下降。一階導數告訴我們在某一特定點上函數是下降還是上升。基本上,一階導數提供正切于誤差平面上一點的一條直線。
什么是函數的梯度?
梯度不過是一個向量,該向量是導數(dy/dx)的多元推廣。導數(dy/dx)則是y相對于x的即時變化率。主要的區別在于,梯度用于計算多元函數的導數,通過偏導數計算。另一個主要的區別是,函數的梯度生成向量場。
梯度由雅可比矩陣表示——一個包含一階偏導數(梯度)的矩陣。
簡單來說,導數定義在單元函數上,而梯度定義在多元函數上。我們就不討論更多關于微積分和物理的內容了。
二階優化算法(Second Order Optimization Algorithms)
二階方法使用二階導數最小化或最大化損失函數。二階方法使用海森矩陣——一個包含二階偏導數的矩陣。由于計算二階導數開銷較大,二階方法不如一階方法常用。二階導數告訴我們一階導數是上升還是下降,這提示了函數的曲率。二階導數提供了一個擬合誤差平面曲率的二次平面。
盡管二階導數計算起來開銷較大,但二階優化算法的優勢在于它沒有忽略誤差平面的曲率。另外,就每一步的表現而言,二階優化算法要比一階優化算法更好。
了解更多關于二階優化算法的內容:https://web.stanford.edu/class/msande311/lecture13.pdf
應該使用哪類優化算法?
目前而言,一階優化技術更容易計算,花費時間更少,在大型數據集上收斂得相當快。
僅當二階導數已知時,二階技術更快,否則這類方法總是更慢,并且計算的開銷更大(無論是時間還是內存)。
不過,有時牛頓二階優化算法能超過一階梯度下降,因為二階技術不會陷入鞍點附近的緩慢收斂路徑,而梯度下降有時會陷進去,無法收斂。
知道哪類算法收斂更快的最好辦法是自己親自嘗試。
梯度下降
梯度下降是訓練和優化智能系統的基礎和最重要技術。
哦,梯度下降——找到最小值,控制方差,接著更新模型的參數,最終帶領我們走向收斂
θ=θ?η??J(θ)是參數更新的公式,其中η為學習率,?J(θ)為損失函數J(θ)在參數θ上的梯度。
梯度下降是優化神經網絡的最流行算法,主要用于更新神經網絡模型的權重,也就是以某個方向更新、調整模型參數,以便最小化損失函數。
我們都知道訓練神經網絡基于一種稱為反向傳播的著名技術。在神經網絡的訓練中,我們首先進行前向傳播,計算輸入信號和相應權重的點積,接著應用激活函數,激活函數在將輸入信號轉換為輸出信號的過程中引入了非線性,這對模型而言非常重要,使得模型幾乎能夠學習任意函數映射。在此之后,我們反向傳播網絡的誤差,基于梯度下降更新權重值,也就是說,我們計算誤差函數(E)在權重(W)也就是參數上的梯度,然后以損失函數的梯度的相反方向更新參數(這里是權重)。
權重在梯度的反方向上更新
上圖中,U型曲線是梯度(坡度)。如你所見,如果權重(W)值過小或過大,那么我們會有較大誤差,所以我們想要更新和優化權重使其既不過小又不過大,所以我們沿著梯度的反方向下降,直到找到局部極小值。
梯度下降的變體
傳統的梯度下降將為整個數據集計算梯度,但僅僅進行一次更新,因此它非常慢,而在大到內存放不下的數據集上更是困難重重。更新的大小由學習率η決定,同時保證能夠在凸誤差平面上收斂到全局最小值,在非凸誤差平面上收斂到局部極小值。另外,標準的梯度下降在大型數據集上計算冗余的更新。
以上標準梯度下降的問題在隨機梯度下降中得到了修正。
1. 隨機梯度下降
隨機梯度下降(SGD)則為每一個訓練樣本進行參數更新。通常它是一個快得多的技術。它每次進行一項更新。
θ=θ?η??J(θ;x(i);y(i))
由于這些頻繁的更新,參數更新具有高方差,從而導致損失函數劇烈波動。這實際上是一件好事,因為它幫助我們發現新的可能更好的局部極小值,而標準隨機梯度下降則如前所述,僅僅收斂至盆地(basin)的極小值。
然而,SGD的問題在于,由于頻繁的更新和波動,它最終復雜化了收斂過程,因頻繁的波動而會不斷越過頭。
不過,如果我們緩慢降低學習率η,SGD展現出和標準梯度下降一樣的收斂模式。
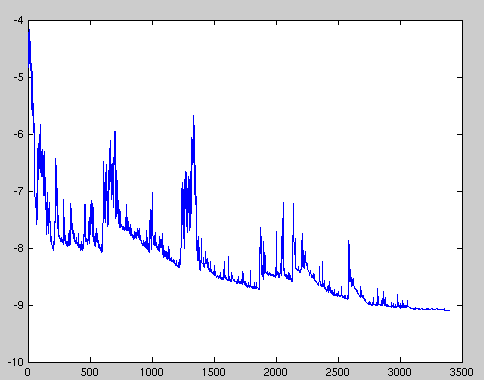
損失函數劇烈波動導致我們可能無法得到最小化損失值的參數
高方差參數更新和不穩定收斂在另一個稱為小批量梯度下降(Mini-Batch Gradient Descent)的變體中得到了修正。
2. 小批量梯度下降
想要避免SGD和標準梯度下降的所有問題和短處,可以使用小批量梯度下降,它吸收了兩種技術的長處,每次進行批量更新。
使用小批量梯度下降的優勢在于:
降低了參數更新的方差,最終導向更好、更穩定的收斂。
可以利用當前最先進的深度學習庫中常見的高度優化的矩陣操作,極為高效地計算小批量梯度。
常用的Mini-batch大小為50到256,不過可能因為應用和問題的不同而不同。
小批量梯度下降是今時今日訓練神經網絡的典型選擇。
P.S. 實際上,很多時候SGD指的就是小批量梯度下降。
梯度下降及其變體面臨的挑戰
選擇合適的學習率可能很難。過小的學習率導致慢到讓人懷疑人生的收斂,在尋找最小化損失的最優參數值時邁著嬰兒般的小步,直接影響總訓練時長,使其過于漫長。而過大的學習率可能阻礙收斂,導致損失函數在極小值周圍波動,甚至走上發散的不歸路。
此外,同樣的學習率應用于所有參數更新。如果我們的數據是稀疏的,我們的特征有非常不同的頻率,我們可能不想以同等程度更新所有特征,而是想在很少出現的特征上進行較大的更新。
最小化神經網絡中常見的高度非凸誤差函數的另一項關鍵挑戰是避免陷入眾多的次優局部極小值。事實上,困難不僅在于局部極小值,更在于鞍點,即一個維度的坡度上升,另一個維度的坡度下降的點。這些鞍點通常被誤差相等的高原環繞,眾所周知,這讓SGD難以逃離,因為在所有維度上,梯度都接近零。
優化梯度下降
現在我們將討論進一步優化梯度下降的多種算法。
動量
SGD的高方差振蕩使其難以收斂,所以人們發明了一項稱為動量(Momentum)的技術,通過在相關方向上導航并減緩非相關方向上的振蕩加速SGD。換句話說,它在當前更新向量中增加了上一步的更新向量,乘以一個系數γ。
V(t)=γV(t?1)+η?J(θ)
最終我們通過θ=θ?V(t)更新參數。
動量項γ通常設為0.9,或與之相似的值。
這里的動量源自經典物理學中的動量概念,當我們沿著一座小山坡向下扔球時,球在沿著山坡向下滾動的過程中收集動量,速度不斷增加。
我們的參數更新過程發生了同樣的事情:
它導向更快、更穩定的收斂。
它減少了振蕩。
動量項γ在梯度指向同一方向的維度上擴大更新,而在梯度方向改變的維度上縮小更新。這減少了不必要的參數更新,導向更快、更穩定的收斂,減少了振蕩。
Nesterov加速梯度
Yurii Nesterov發現了動量的一個問題:
盲目地隨著坡度滾下山坡的球是不令人滿意的。我們希望能有一個智能一點的球,對所處位置有一定的概念,知道在坡度變得向上前減速。
也就是說,當我們到達極小值,也就是曲線的最低點時,動量相當高,因為高動量的作用,優化算法并不知道在那一點減速,這可能導致優化算法完全錯過極小值然后接著向上移動。
Yurii Nesterov在1983年發表了一篇論文,解決了動量的這個問題。我們現在將其提出的策略稱為Nesterov加速梯度(Nestrov Accelerated Gradient,NAG)。
Nesterov提議,我們首先基于先前的動量進行一次大跳躍,接著計算梯度,然后據此作出修正,并根據修正更新參數。預更新可以防止優化算法走得太快錯過極小值,使其對變動的反應更靈敏。
NAG是為動量項提供預知能力的一種方法。我們知道,我們在更新參數θ的時候會用到動量項γV(t?1)。因此,計算θ?γV(t?1)能提供參數下一位置的近似值。這樣我們就可以通過計算參數未來位置的近似值上的梯度“預見未來”:
V(t)=γV(t?1)+η?J( θ?γV(t?1) )
接著我們同樣通過θ=θ?V(t)更新參數。
關于NAG的更多細節,可以參考cs231n課程。
現在,我們已經能夠根據誤差函數的斜率調整更新的幅度,并加速SGD過程,我們同樣希望能根據不同參數的重要性調整更新的幅度。
Adagrad
Adagrad讓學習率η可以基于參數調整,為不頻繁的參數進行較大的更新,為頻繁的參數進行較小的更新。因此,它很適合處理稀疏數據。
Adagrad在每一時步為每個參數θ使用不同的學習率,學習率的大小基于該參數的過往梯度。
之前,我們為所有參數θ一下子進行更新,因為每個參數θ(i)使用相同的學習率η。由于Adagrad在每個時步t為每個參數θ(i)使用不同的學習率,我們首先計算Adagrad在每個參數上的更新,接著將其向量化。設gi,t為參數θ(i)在時步t的損失函數的梯度,則Adagrad的公式為:
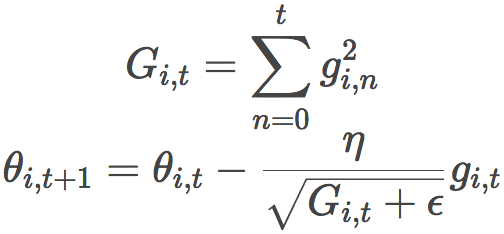
上式中,?為平滑因子,避免除數為零。
從上式中,我們可以看到:
某方向上的Gi,t較小,則相應的學習率較大,也就是說,為不頻繁出現的參數做較大的更新。
隨著時間的推移,Gi,t越來越大,從而使學習率越來越小。因此,我們無需手動調整學習率。大多數Adagrad的實現中,η均使用默認值0.01. 這是Adagrad的一大優勢。
由于Gi,t為平方和,每一項都是正值。因此,隨著訓練過程的進行,Gi,t會持續不斷地增長。這意味著,學習率會持續不斷地下降,模型收斂越來越慢,訓練需要漫長的時間,甚至最終學習率小到模型完全停止學習。這是Adagrad的主要缺陷。
另一個算法AdaDelta修正了Adagrad的學習率衰減問題。
AdaDelta
AdaDelta試圖解決Adagrad的學習率衰減問題。不像Adagrad累加所有過往平方梯度,Adadelta對累加的范圍作了限制,只累計固定大小w的窗口內的過往梯度。 為了提升效率,Adadelta也沒有存儲w個平方梯度,而是過往平方梯度的均值。這樣,時步t的動態均值就只取決于先前的均值和當前梯度。
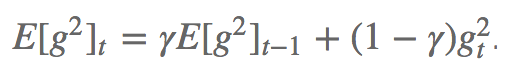
其中,γ的取值和動量方法類似,在0.9左右。
類似Adagrad,Adadelta的公式為:
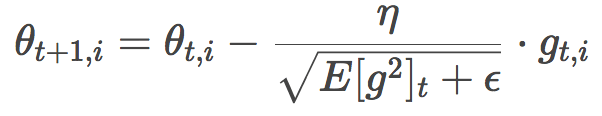
由于分母部分恰好符合梯度的均方誤差的定義:
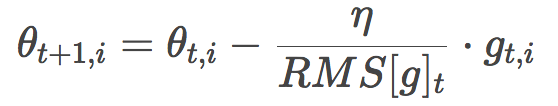
這其實也是RMSprop的公式。RMSprop是由Geoffrey Hinton提出的,未以論文形式發表,見其csc321課程。
Adadelta和RMSProp是在差不多同時相互獨立地開發的,都是為了解決Adagrad的學習率衰減問題。
另外,標準的Adadelta算法中,和分母對稱,分子的η也可以用RMS[Δθ]t-1替換:
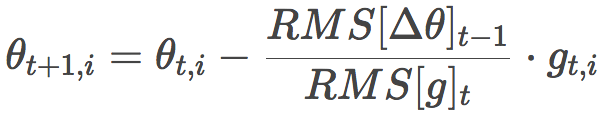
這就消去了η!也就是說,我們無需指定η的值了。
目前為止我們所做的改進
為每個參數計算不同的學習率。
同時計算動量。
防止學習率衰減。
還有什么可以改進的?
既然我們已經為每個參數分別計算學習率,為什么不為每個參數分別計算動量變動呢?基于這一想法,人們提出了Adam優化算法。
Adam
Adam表示自適應動量估計(Adaptive Moment Estimation)。
開門見山,讓我們直接查看Adam的公式:
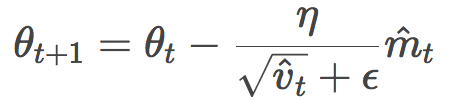
有沒有一種似曾相識的感覺?你的感覺沒錯,這很像RMSProp或者Adadelta的公式:
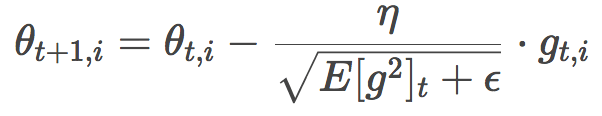
所以,問題來了,這vt和mt到底是什么玩意?莫急,我們馬上給出兩者的定義。
先來瞧瞧vt:
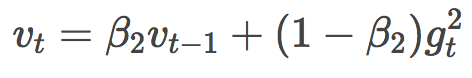
喲!這不就是Adadelta或者RMSProp里面的過往平方梯度均值嘛!只不過換了幾個字母,把γ換成了β2,把E[g2]換成了v。
再來看看mt的定義:
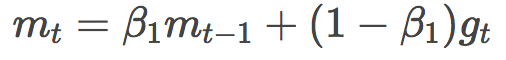
咦?這個好像和動量的定義有點像呀?
V(t)=γV(t?1)+η?J(θ)
γ換成了β1,?J(θ)和gt都是梯度。當然還有一個系數不一樣,只是有點像,不是一回事。
從這個角度來說,Adam算法有點博采眾家之長的意思。事實上,RMSProp或者Adadelta可以看成是Adam算法不帶動量的特殊情形。
當然,其實我們上面有一個地方漏了沒說。細心的讀者可能已經發現,實際上Adam的公式里vt和mt是戴帽的,這頂帽子意義何在?
這是因為,作者發現,由于vt和mt剛開始初始化為全零向量,會導致這兩個量的估計向零傾斜,特別是在剛開始的幾個時步里,以及衰減率很小的情況下(即β取值接近1)。因此需要額外加上校正步驟:
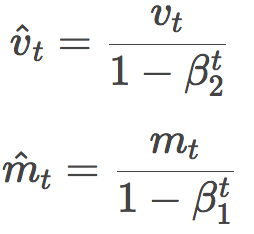
Adam作者建議,β1取0.9,β2取0.999,?取10-8。
在實踐中,Adam的表現非常出色,收斂迅速,也修正了之前一些優化算法的問題,比如學習率衰減、收斂緩慢、損失函數振蕩。通常而言,Adam是自適應學習率算法的較優選擇。
AMSGrad
在ICLR 2018上,Google的Reddi等提交了一篇關于Adam收斂性的論文,指出了Adam算法收斂性證明中的一個錯誤。并構造了一個簡單的凸優化問題作為反例,證明Adam在其上無法收斂。另外,Reddi等提出了Adam算法的一個變體,AMSGRad,其主要改動為:
基于算法的簡單性考量,去除了Adam的偏置糾正步驟。
僅當當前vt大于vt-1時,才應用vt。也就是說,應用兩種中較大的那個。這有助于避免收斂至次優解時,某些提供較大、有用梯度的罕見mini-batch的作用可能被過往平方梯度均值大為削弱,導致難以收斂的問題。
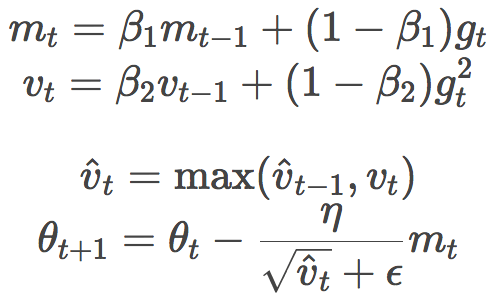
Reddi等在小型網絡(MNIST上的單層MLP、CIFAR-10上的小型卷積網絡)上展示了AMSGrad在訓練損失和測試損失方面相對Adam的優勢。然而,有人在較大模型上進行了試驗,發現兩者并無顯著差異(順便,Adam和AMSGrad的偏置糾正是否開啟,影響也不大)。
可視化優化算法
下面讓我們來看兩張動圖,希望它們有助于直觀地理解網絡的訓練過程。
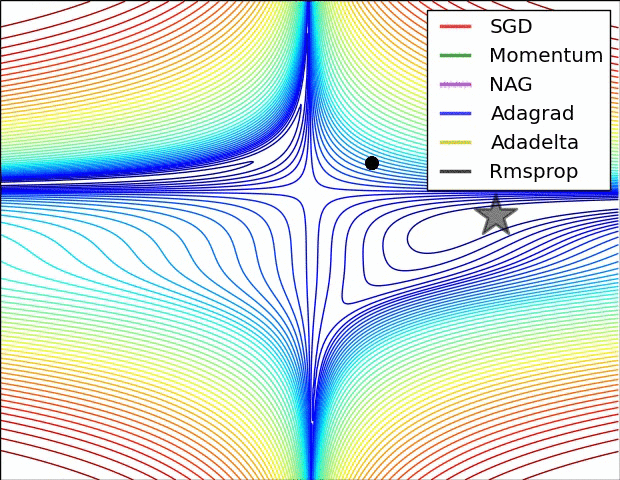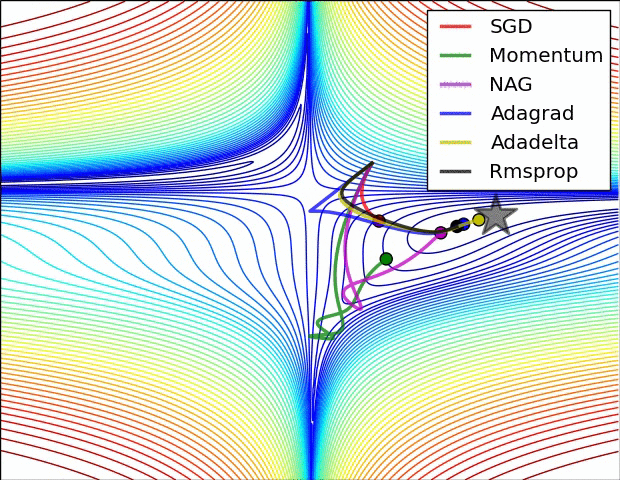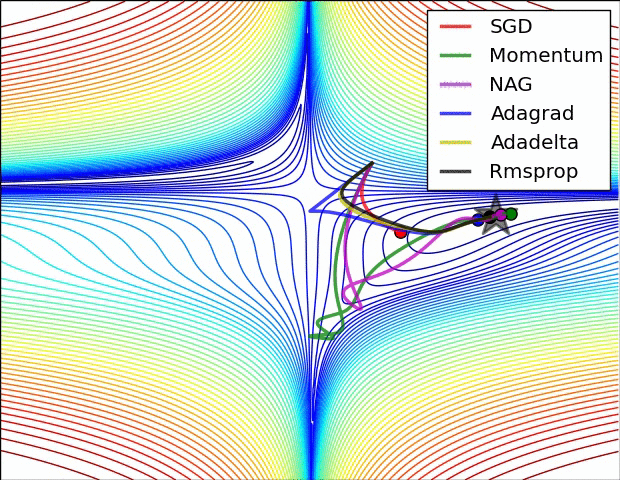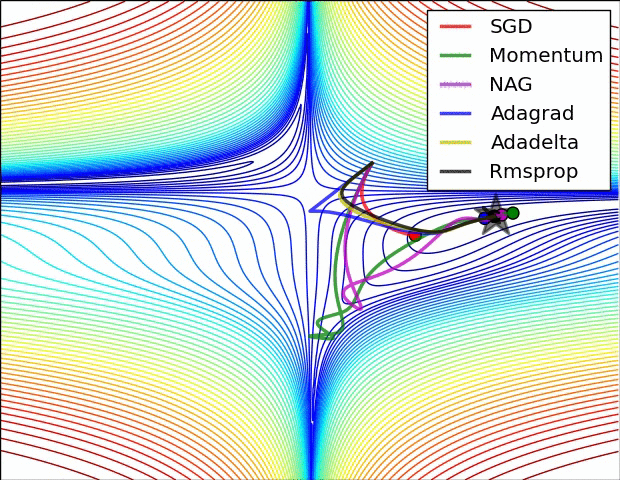
上圖為誤差平面的等值線圖。從圖中我們可以看到,自適應學習率方法干凈利落地完成了收斂。而SGD、動量法、NAG收斂十分緩慢。其中,動量法和NAG在動量的作用下,歡快地朝著一個方向狂奔,相比之下,NAG更快反應過來。SGD倒是沒有沖過頭,可惜最后沒能收斂到最優值。

上圖演示了不同優化算法在鞍點的表現。我們看到,自適應學習率方法毫不拖泥帶水地擺脫了鞍點,動量法、NAG在鞍點徘徊良久后終于逃出生天,而SGD最終陷在鞍點無法自拔。
以上兩幅動圖均由Alec Radford制作。
應該使用哪種優化算法?
不幸的是,這一問題目前還沒有明確的答案。這里僅能提供一些建議:
目前而言,用的比較多的優化算法是SGD、動量、RMSProp、AdaDelta、Adam。
在稀疏數據上,一般建議使用自適應學習率算法。
在高度復雜的模型上,推薦使用自適應學習率算法,通常它們收斂起來比較快。
在其他問題中,使用自適應學習率算法通常也能取得較優的表現。同時它也額外帶來了一項福利:你不用操心學習率設定問題。
總體而言,在自適應學習率算法中,Adam是一個比較流行的選擇。
考慮到超參數調整的便利性,優化算法的選擇還取決于你對不同算法的熟悉程度。
Adam在不同超參數下的魯棒性較好,不過有時你可能需要調整下η值。
-
神經網絡
+關注
關注
42文章
4776瀏覽量
100938 -
優化算法
+關注
關注
0文章
35瀏覽量
9700 -
函數
+關注
關注
3文章
4340瀏覽量
62793
原文標題:梯度下降優化之旅:神經網絡常用優化算法概覽
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
粒子群優化模糊神經網絡在語音識別中的應用
如何構建神經網絡?
卷積神經網絡模型發展及應用
改進人工蜂群算法優化RBF神經網絡的短時交通流預測模型
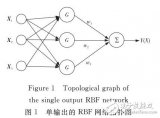




 神經網絡模型使用什么樣的優化算法?
神經網絡模型使用什么樣的優化算法?










評論