Cheng-Tao Chu總結了機器學習建模中常見的誤區,提醒讀者注意算法的假定未必適合手頭的數據。Chu曾任Google欺詐支付分析首席工程師,LinkedIn搜索相關性負責人,Square欺詐檢測負責人,Codecademy數據分析主管,現為都鐸投資公司下一代研究、模擬、交易基礎設施MacroPipeline的首席架構師。Chu在NIPS 2006的論文“基于多核的機器學習Map-Reduce”引用超過1400次,是開源項目Apache Mahout的基礎。
統計建模和工程有許多相似之處。
在工程上,有多種方法構建一個鍵值存儲,而每種設計對使用模式有著不同的假設。在統計建模中,有多種算法構建一個分類器,而每種算法對數據有著不同的假設。
當處理小規模數據時,由于試驗的成本較低,盡可能多地嘗試各種算法然后選出最好的算法,是很合理的選擇。但是當我們碰到“大數據”的時候,事先分析數據并據此設計建模流程(預處理、建模、優化算法、評估、產品化),會有很大幫助。
我在前一篇博客文章就提到了,有幾十種方法解決一個給定的建模問題。每種模型有著不同的假定,辨識哪些假設合理,并沒有顯而易見的方法。在業界,大多數從業人員選擇他們最熟悉的建模算法,而不是最適合數據的算法。在這篇文章中,我想要分享一些常見的誤區,至于最佳實踐,留待以后的文章。
1. 理所當然地使用默認損失函數
很多從業人員在訓練和挑選模型的時候使用默認的損失函數(例如,均方誤差)。在實踐中,默認的損失函數很少對齊業務的目標。就拿欺詐檢測來說吧。當嘗試檢測欺詐性交易時,業務目標是最小化欺詐的損失。而二元分類器的默認損失函數給予假陽性和假陰性同樣的權重。為了對齊業務目標,損失函數不僅應該加大懲罰假陰性的力度,同時懲罰假陰性的力度也應該和損失金額成比例。此外,欺詐檢測中的數據集通常包含高度失衡的標簽。在這些情形下,損失函數需要向罕見類別方向傾斜。
2. 在非線性相互作用中使用原始的線性模型
構建二元分類器時,出于簡單性,許多從業人員立刻拿出邏輯回歸。不過,很多人忘了,邏輯回歸是一個線性模型,因此需要手工編碼預測因子中的非線性相互作用。回到欺詐性檢測的例子,“賬單地址 = 配送地址且交易額 < $50”這樣的高階相互作用特征對良好的模型表現而言不可或缺。所以,這類問題應該考慮非線性模型,比如配有核函數的SVM、基于決策樹的分類器這樣內置高階相互作用特征支持的模型。
3. 忘了離群值
離群值值得注意。取決于上下文,它們或者需要特別關注,或者應該完全忽略。以利潤預測為例。如果觀察到了不同尋常的利率尖峰,對其給予額外關注,查明導致尖峰的原因,應該是個好主意。不過如果離群值是由機制誤差、測量誤差或其他任何不可推廣的原因造成的,那么,在將數據傳給建模算法前,過濾掉這些離群值是個好主意。
相比其他模型,一些模型對離群值更敏感。比如,AdaBoost可能會將那些離群值視作“困難”情形,給予離群值巨大的權重,而決策樹可能僅僅將每個離群值視作假分類。如果數據集包含相當數量的離群值,需要使用在離群值上魯棒性好的建模算法,或者過濾掉離群值,這一點很重要。
4. 當n遠小于p時使用高方差模型
SVM是最流行的現成的建模算法之一,而其最強力的特性之一是使用不同的核調整模型。SVM的核可以看成一種自動組合現有特征至更豐富的特征空間的方法。由于這一強力特性幾乎沒什么代價,大多數從業人員在訓練SVM模型時默認使用核。然而,當n << p(樣本數遠小于特征數)時——在業界很常見,比如醫療數據——更豐富的特征空間意味著高得多的過擬合數據的風險。事實上,當n << p時,應該完全避免高方差模型。
5. 使用L1/L2/...正則化時不做標準化
應用L1或L2懲罰大系數是常用的正則化線性回歸或邏輯回歸的方法。然而,許多從業人員沒有意識到在應用這些正則化技術之前標準化特征的重要性。
回到欺詐檢測的例子,想象一個交易額特征的線性回歸模型。在沒有正則化的情況下,如果交易額的單位是元,擬合的參數大概會是單位是分的情況下擬合的參數的一百倍。而在有正則化的情況下,由于L1/L2對較大系數懲罰的力度更大,以元為單位的交易額會受到更多懲罰。因此,正則化出現了偏差,傾向于懲罰尺度較小的特征。為了緩解這一問題,在預處理步驟中標準化所有特征,讓它們位于同一水平線上。
6. 使用線性模型時沒有考慮多重共線性
想象一下,創建一個包含兩個變量X1、X2的線性模型,假定標準答案是Y = X1+ X2。理想情況下,如果觀測數據的噪聲不大,線性回歸方案將重建標準答案。然而,如果X1和X2共線,那么在大多數優化算法看來,Y = 2 * X1、Y = 3 * X1- X2、Y = 100 * X1- 99 * X2都很不錯。這可能不會造成什么妨害,因為它并未導致估計出現偏差。不過,它確實造成了不良的狀況,使得系數的權重難以解釋。
7. 將線性回歸或邏輯回歸的系數絕對值視作特征重要性
因為很多現成的線性回歸器返回每個系數的p值,許多從業人員相信,線性模型的系數的絕對值越大,相應的特征就越重要。其實這極少成立:
改變變量的尺度會改變系數的絕對值
如果特征具有多重共線性,系數可以從一個特征移動到其他特征。同時,數據集的特征越多,特征具有多重共線性的概率就越高,通過系數解釋特征重要性就越不可靠。
以上是機器學習實踐中常見的7個誤區。這個列表并不求全,主要用意是激發讀者的思考,建模的假定可能并不適用于手頭的數據。為了達到最佳的模型表現,選擇具有最合適的假定的建模算法很重要——而不是直接選擇你最熟悉的算法。
-
機器學習
+關注
關注
66文章
8418瀏覽量
132635
原文標題:老司機帶你避開機器學習那些坑
文章出處:【微信號:jqr_AI,微信公眾號:論智】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 淺析機器學習建模中常見的7個誤區
淺析機器學習建模中常見的7個誤區
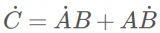












評論