眾所周知,神經(jīng)網(wǎng)絡(luò)可以學(xué)習(xí)如何表示和處理數(shù)字式信息,但是如果在訓(xùn)練當(dāng)中遇到超出可接受的數(shù)值范圍,它歸納信息的能力很難保持在一個較好的水平。為了推廣更加系統(tǒng)化的數(shù)值外推,我們提出了一種新的架構(gòu),它將數(shù)字式信息表示為線性激活函數(shù),使用原始算術(shù)運(yùn)算符進(jìn)行運(yùn)算,并由學(xué)習(xí)門控制。我們將此模塊稱為神經(jīng)算術(shù)邏輯單元(NALU),類似于傳統(tǒng)處理器中的算術(shù)邏輯單元。實(shí)驗表明,增強(qiáng)的NALU神經(jīng)網(wǎng)絡(luò)可以學(xué)習(xí)時間追蹤,使用算術(shù)對數(shù)字式圖像進(jìn)行處理,將數(shù)字式信息轉(zhuǎn)為實(shí)值標(biāo)量,執(zhí)行計算機(jī)代碼以及獲取圖像中的目標(biāo)個數(shù)。與傳統(tǒng)的架構(gòu)相比,我們在訓(xùn)練過程中不管在數(shù)值范圍內(nèi)還是外都可以更好的泛化,并且外推經(jīng)常能超出訓(xùn)練數(shù)值范圍的幾個數(shù)量級之外。
▌簡介
對數(shù)值表示和處理的能力在許多物種中普遍可見,這表明基本的定量推理是智力的一個組成部分。雖然神經(jīng)網(wǎng)絡(luò)可以在給定適當(dāng)?shù)膶W(xué)習(xí)信號的情況下成功地表示和處理數(shù)值量,但它們的學(xué)習(xí)行為缺乏系統(tǒng)的泛化。具體而言,當(dāng)測試階段的數(shù)值超出了訓(xùn)練階段的數(shù)值范圍,即使目標(biāo)函數(shù)很簡單也會導(dǎo)致出錯。這表明學(xué)習(xí)行為的特點(diǎn)是記憶而不是系統(tǒng)抽象。
在本文中,我們設(shè)計了一個偏向于學(xué)習(xí)系統(tǒng)數(shù)值計算的新模塊,該模塊可以與標(biāo)準(zhǔn)的神經(jīng)網(wǎng)絡(luò)體系結(jié)構(gòu)結(jié)合使用。我們的策略是將數(shù)值表示為無非線性的單個神經(jīng)元,其中這些單值神經(jīng)元采用的是類似于加減乘除的運(yùn)算符來表示,運(yùn)算符由參數(shù)來控制。
神經(jīng)網(wǎng)絡(luò)中的數(shù)值外推失效
為了說明標(biāo)準(zhǔn)網(wǎng)絡(luò)中的系統(tǒng)性失效,我們展示了各種MLPs在學(xué)習(xí)標(biāo)量恒等函數(shù)的表現(xiàn)。圖1表明即使采用簡單的框架,所有非線性函數(shù)都無法學(xué)習(xí)到超出訓(xùn)練范圍外的數(shù)量表示。
圖1 MLPs在學(xué)習(xí)標(biāo)量恒等函數(shù)時的表現(xiàn)
▌神經(jīng)累加器和神經(jīng)算術(shù)邏輯單元
本文,我們提出了兩種能夠?qū)W習(xí)以系統(tǒng)的方式去表示和處理數(shù)字式信息的模型。第一種模型有支持對積累量進(jìn)行累加的能力,這是線性外推的理想偏置項。該模型構(gòu)成了第二個模型的基礎(chǔ),即支持乘法外推。此模型還闡述了如何將任意算術(shù)函數(shù)的偏置項有效地融合到端到端模型中。
第一個模型是神經(jīng)累加器(NAC),它是線性(仿射)層的一種特殊應(yīng)用,其變換矩陣W只由-1,0和1組成。也就是說,它的輸出是輸入向量中行的加減算法,這也能夠預(yù)防層在將輸入映射到輸出時改變數(shù)字的表示比例。
由于硬性的約束W矩陣中的每個元素都為{-1,0,0},這使得模型在學(xué)習(xí)中變得更加困難。為此我們提出了一種W在無參數(shù)約束條件下的連續(xù)可微分參數(shù)化方法: 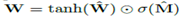 。該方法給梯度下降學(xué)習(xí)帶來了很大的方便,同時產(chǎn)生一個元素在[-1,1]?并且趨向于-1,0或1的矩陣。圖2描述了一個神經(jīng)算術(shù)邏輯單元(NALU),它可以學(xué)習(xí)兩個子單元間的加權(quán)和,一個能夠進(jìn)行加減運(yùn)算,另一個則可以執(zhí)行乘除以及冪運(yùn)算,如
。該方法給梯度下降學(xué)習(xí)帶來了很大的方便,同時產(chǎn)生一個元素在[-1,1]?并且趨向于-1,0或1的矩陣。圖2描述了一個神經(jīng)算術(shù)邏輯單元(NALU),它可以學(xué)習(xí)兩個子單元間的加權(quán)和,一個能夠進(jìn)行加減運(yùn)算,另一個則可以執(zhí)行乘除以及冪運(yùn)算,如 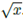 。更重要的優(yōu)點(diǎn)是,其能夠展示如何在門控的子操作中擴(kuò)展NAC,從而增強(qiáng)了新類型數(shù)值函數(shù)的端到端學(xué)習(xí)。
。更重要的優(yōu)點(diǎn)是,其能夠展示如何在門控的子操作中擴(kuò)展NAC,從而增強(qiáng)了新類型數(shù)值函數(shù)的端到端學(xué)習(xí)。
圖2(a)神經(jīng)累加器(b)神經(jīng)算術(shù)邏輯單元
圖2中,NAC是輸入的一次線性變換,變換矩陣是tanh(W)和 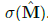 元素的乘積。NALU?使用兩個帶有固定系數(shù)的NACs?來進(jìn)行加減運(yùn)算(圖2中較小的紫色單元)?以及乘除運(yùn)算(圖2中較大的紫色單元),并由門(圖2中橙色的單元)來控制。
元素的乘積。NALU?使用兩個帶有固定系數(shù)的NACs?來進(jìn)行加減運(yùn)算(圖2中較小的紫色單元)?以及乘除運(yùn)算(圖2中較大的紫色單元),并由門(圖2中橙色的單元)來控制。
▌實(shí)驗
我們跨域各種任務(wù)領(lǐng)域 (圖像、文本、代碼等),學(xué)習(xí)信號 (監(jiān)督和強(qiáng)化學(xué)習(xí)),結(jié)構(gòu) (前饋和循環(huán)) 進(jìn)行實(shí)驗,結(jié)果表明我們提出的模型可以學(xué)習(xí)到數(shù)據(jù)中潛在數(shù)值性質(zhì)的表示函數(shù),并推廣到比訓(xùn)練階段的數(shù)值大幾個數(shù)量級的數(shù)值。相比于線性層我們的模塊有更小的計算偏差。在一個具體實(shí)例中,我們的模型超過了目前最先進(jìn)的圖像計數(shù)網(wǎng)絡(luò),值得一提的是,我們所做的修改僅是用我們的模型替換了其最后一個線性層。
簡單的函數(shù)學(xué)習(xí)任務(wù)
在這些初始合成實(shí)驗中,我們展示了NAC和NALU在學(xué)習(xí)選擇相關(guān)輸入并應(yīng)用不同算術(shù)函數(shù)的能力。其中測試任務(wù)分為兩類:第一類為靜態(tài)任務(wù),即以單個向量一次性輸入;第二類是循環(huán)任務(wù),即輸入按時間順序來呈現(xiàn)。通過最小化平方損失來端到端地訓(xùn)練模型,模型的性能評估由兩個部分組成:訓(xùn)練范圍內(nèi)(插值)的留存值和訓(xùn)練范圍外(外推)的值。表1表明了幾種標(biāo)準(zhǔn)體系結(jié)構(gòu)在插值情況下成功完成任務(wù),但在進(jìn)行外推時都沒有成功。而不管是在插值還是外推上,NAC都成功地建立加法和減法模型,NALU在乘法運(yùn)算上也獲得成功。
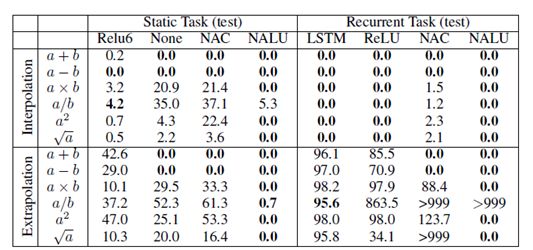
表 1 靜態(tài)和循環(huán)任務(wù)的插值和外推誤差率
MNIST 計數(shù)和算術(shù)任務(wù)
在這項任務(wù)中,我們給模型10個隨機(jī)選擇的MNIST數(shù)字,要求模型輸出觀察到的數(shù)值和每種類型的圖像數(shù)量,在MNIST數(shù)字加法任務(wù)中,模型還必須學(xué)會計算所觀察到的數(shù)字之和。在插值(長度為10)和外推(長度為100和長度為1000)任務(wù)上測試模型的計數(shù)和算術(shù)的性能。表2表明標(biāo)準(zhǔn)體系結(jié)構(gòu)在插值任務(wù)上成功,但在外推任務(wù)上失敗。但是NAC和NALU都能很好地完成插值和外推任務(wù)。
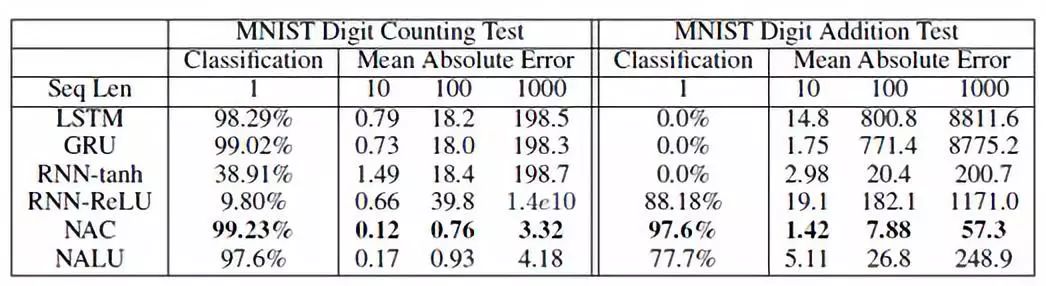
表2 長度為1,100,1000的序列的 MNIST 計數(shù)和加法任務(wù)的準(zhǔn)確度
語言到數(shù)字的翻譯任務(wù)
為了測試數(shù)字詞語的表示是否是以系統(tǒng)的形式來學(xué)習(xí),我們設(shè)計了一個新的翻譯任務(wù):將文本數(shù)字表達(dá)式(例如五百一十五)轉(zhuǎn)換為標(biāo)量表示(515)。訓(xùn)練和測試的數(shù)字范圍在0到1000之間,其中訓(xùn)練集、驗證集和測試集的示例分別為169、200和631。在該數(shù)據(jù)集上訓(xùn)練的所有網(wǎng)絡(luò)都以embedding層開始,通過LSTM進(jìn)行編碼,最后接一個NAC或NALU。表3表明了LSTM + NAC在訓(xùn)練和測試集上都表現(xiàn)不佳。LSTM + NALU可以大幅度地實(shí)現(xiàn)最佳的泛化性能,這說明乘數(shù)對于此任務(wù)來說非常重要。這里還給出了一個NALU測試的例子如圖3所示。

表3將數(shù)字串轉(zhuǎn)換為標(biāo)量的平均絕對誤差(MSE)比較

圖3 NALU的預(yù)測樣例
程序評估
程序評估部分我們考慮兩個方面:第一個為簡單地添加兩個大整數(shù),第二個為包含若干個操作(條件聲明、加和減)。此次評估專注于外推部分即:網(wǎng)絡(luò)是否可以學(xué)習(xí)一種推廣到更大數(shù)值范圍的解決方案。用[0,100)范圍內(nèi)的兩位數(shù)整數(shù)來訓(xùn)練,并用三位或四位的隨機(jī)整數(shù)來評估。圖4比較了四種不同模型(UGRNN、LSTM、DNC和NALU)的評估結(jié)果,其中只有NALU是能夠推廣到更大的數(shù)字。我們可以看到即使域增加了兩個數(shù)量級,外推效果也是較為穩(wěn)定。
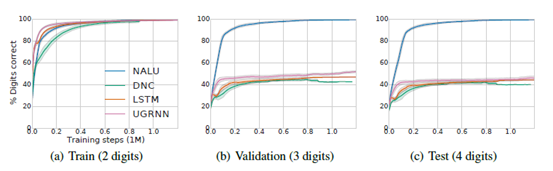
圖4簡單的程序評估,外推到更大的值
學(xué)習(xí)在網(wǎng)格世界環(huán)境中追蹤時間
到目前為止,在所有實(shí)驗中,我們訓(xùn)練的模型已經(jīng)可以進(jìn)行數(shù)值預(yù)測了。然而,正如引言部分所說,系統(tǒng)化的數(shù)值推算似乎是各種智能行為的基礎(chǔ)。因此,我們進(jìn)行了一項任務(wù),測試NAC能否被RL-trained智能體“內(nèi)部”使用。
如圖5所示,該任務(wù)中,每一幀都是從初始值開始(t=0),紅色的目標(biāo)隨機(jī)定位于5*5的網(wǎng)絡(luò)世界方格中。每個時間步中,智能體接收一個56*56像素網(wǎng)格以表示整個網(wǎng)格世界環(huán)境狀態(tài),并且必須從{上移,下移,左移,右移,忽略}選擇其中的一個操作。測試開始前,智能體還會接收一個數(shù)字(整數(shù))指令T ,用來傳達(dá)代理到底目的地的確切時間。
達(dá)到最大幀時,獎勵m,智能體必須選擇操作并四處移動。第一次移動至紅色區(qū)域時就是t=T的時候,當(dāng)智能體到達(dá)紅色區(qū)域或者時間結(jié)束時(t=L)訓(xùn)練結(jié)束。
圖5網(wǎng)格世界環(huán)境中時間追蹤任務(wù)
MNIST 奇偶校驗預(yù)測任務(wù)和消融研究
在我們的最后一項任務(wù):MNIST奇偶校驗中,輸入和輸出都不是直接用數(shù)字提供的,而是隱式地對數(shù)字量進(jìn)行推理。在這個實(shí)驗中,NAC或其變體取代了由Segui等人提出的模型中的最后一個線性層。我們系統(tǒng)地研究了每個約束的重要性。表4總結(jié)了變體模型的性能,我們可以看到去除偏置項和運(yùn)用非線性權(quán)重的方法顯著提高了端到端模型的準(zhǔn)確性,NAC將先前最佳結(jié)果的誤差減少了54%。
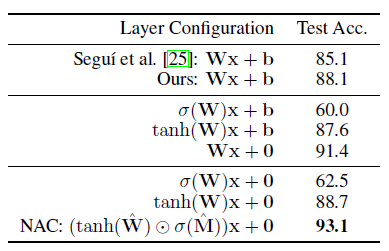
表4關(guān)于MNIST奇偶校驗任務(wù)的affine層和NAC之間的消融研究
▌結(jié)論
目前,神經(jīng)網(wǎng)絡(luò)中數(shù)值模擬方法還不夠完善,因為數(shù)值表示方法不能夠?qū)ζ溆?xùn)練觀察到的數(shù)值范圍外對信息進(jìn)行較好的概括。本文,我們已經(jīng)展示了NAC與NALU是如何解這兩個不足之處,它改善了數(shù)值表示方法以及數(shù)值范圍外的函數(shù)。然而,NAC或NALU不太可能很完美的解決每一個任務(wù)。但它們可以被作為解決創(chuàng)建模型時目標(biāo)函數(shù)存在偏置項的一種通用策略。該策略是由我們提出的單元神經(jīng)數(shù)值表示方式實(shí)現(xiàn)的,它允許將任意(可微)數(shù)值函數(shù)添加到模塊中,并通過學(xué)習(xí)門進(jìn)行控制。
-
神經(jīng)網(wǎng)絡(luò)
+關(guān)注
關(guān)注
42文章
4772瀏覽量
100792 -
神經(jīng)元
+關(guān)注
關(guān)注
1文章
363瀏覽量
18453
原文標(biāo)題:前沿 | DeepMind 最新研究——神經(jīng)算術(shù)邏輯單元,有必要看一下!
文章出處:【微信號:rgznai100,微信公眾號:rgznai100】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
基于可編程邏輯器件和VHDL語言實(shí)現(xiàn)算術(shù)邏輯單元的設(shè)計
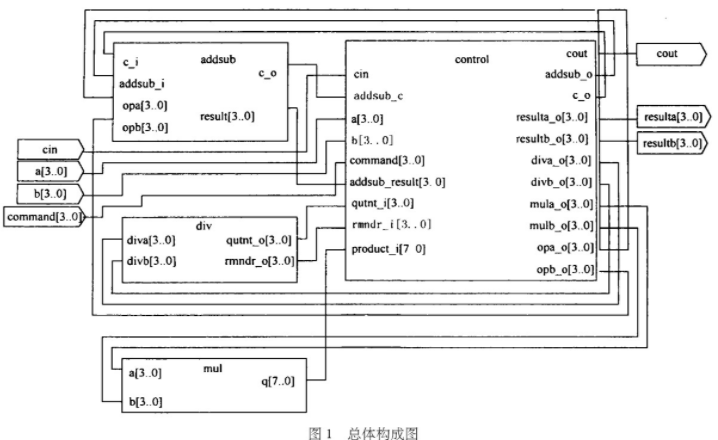
FPGA基礎(chǔ)學(xué)習(xí)筆記--組合邏輯電路-算術(shù)運(yùn)算電路
算術(shù)邏輯單元ALU四個要素
恩智浦eIQ? Neutron神經(jīng)處理單元
TMS320F24X 指令集累加器、算術(shù)與邏輯指令附件
多功能算術(shù)/邏輯運(yùn)算單元(ALU) ,什么是多功能算術(shù)/邏輯
低功耗時鐘門控算術(shù)邏輯單元在不同F(xiàn)PGA中的時鐘能量分析
DeepMind最新提出“神經(jīng)算術(shù)邏輯單元”,旨在解決神經(jīng)網(wǎng)絡(luò)數(shù)值模擬能力不足的問題
51單片機(jī)的算術(shù)和邏輯運(yùn)算功能介紹
詳解邏輯單元的內(nèi)部結(jié)構(gòu)
用VHDL語言創(chuàng)建一個8位算術(shù)邏輯單元(ALU)





 什么是神經(jīng)算術(shù)邏輯單元?
什么是神經(jīng)算術(shù)邏輯單元?










評論