在筆記 4 中,詳細闡述了機器學習中利用正則化防止過擬合的基本方法,對 L1 和 L2 范數進行了通俗的解釋。為了防止深度神經網絡出現過擬合,除了給損失函數加上 L2 正則化項之外,還有一個很著名的方法——dropout.
廢話少說,咱們單刀直入正題。究竟啥是 dropout ? dropout 是指在神經網絡訓練的過程中,對所有神經元按照一定的概率進行消除的處理方式。在訓練深度神經網絡時,dropout 能夠在很大程度上簡化神經網絡結構,防止神經網絡過擬合。所以,從本質上而言,dropout 也是一種神經網絡的正則化方法。
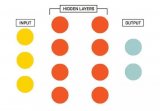
假設我們要訓練了一個 4 層(3個隱層)的神經網絡,該神經網絡存在著過擬合。于是我們決定使用 dropout 方法來處理,dropout 為該網絡每一層的神經元設定一個失活(drop)概率,在神經網絡訓練過程中,我們會丟棄一些神經元節點,在網絡圖上則表示為該神經元節點的進出連線被刪除。最后我們會得到一個神經元更少、模型相對簡單的神經網絡,這樣一來原先的過擬合情況就會大大的得到緩解。這樣說似乎并沒有將 dropout 正則化原理解釋清楚,我們繼續深究一下:為什么 dropout 可以可以通過正則化發揮防止過擬合的功能?
因為 dropout 可以隨時隨機的丟棄任何一個神經元,神經網絡的訓練結果不會依賴于任何一個輸入特征,每一個神經元都以這種方式進行傳播,并為神經元的所有輸入增加一點權重,dropout 通過傳播所有權重產生類似于 L2 正則化收縮權重的平方范數的效果,這樣的權重壓縮類似于 L2 正則化的權值衰減,這種外層的正則化起到了防止過擬合的作用。
所以說,總體而言,dropout 的功能類似于 L2 正則化,但又有所區別。另外需要注意的一點是,對于一個多層的神經網絡,我們的 dropout 某層神經元的概率并不是一刀切的。對于不同神經元個數的神經網絡層,我們可以設置不同的失活或者保留概率,對于含有較多權值的層,我們可以選擇設置較大的失活概率(即較小的保留概率)。所以,總結來說就是如果你擔心某些層所含神經元較多或者比其他層更容易發生過擬合,我們可以將該層的失活概率設置的更高一些。
說了這么多,總算大致把 dropout 說明白了。那 dropout 這種操作在實際的 python 編程中該如何實現呢?以一個三層的神經網絡為例,首先我們需要定義一個 3 層的 dropout 向量,然后將其與保留概率 keep-prob 進行比較生成一個布爾值向量,再將其與該層的神經元激活輸出值進行乘積運算,最后擴展上一步的計算結果,將其除以 keep-prob 即可。但在實際編程中就沒說的這么容易了,我們需要對整個神經網絡的計算過程進行重新定義,包括前向傳播和反向傳播的計算定義。
含 dropout 的前向計算定義如下:
def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
np.random.seed(1) # retrieve parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"] # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
D1 = np.random.rand(A1.shape[0], A1.shape[1])
D1 = D1 < keep_prob ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ?A1 = np.multiply(D1, A1) ? ? ? ? ? ? ? ? ? ? ? ?
? ?A1 = A1 / keep_prob ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ?Z2 = np.dot(W2, A1) + b2
? ?A2 = relu(Z2)
? ?D2 = np.random.rand(A2.shape[0], A2.shape[1])
D2 = D2 < keep_prob ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ?A2 = np.multiply(D2, A2) ? ? ? ? ? ? ? ? ? ? ?
? ?A2 = A2 / keep_prob ? ? ? ? ? ? ? ? ? ? ? ? ?
? ?Z3 = np.dot(W3, A2) + b3
? ?A3 = sigmoid(Z3)
? ?cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) ? ?
return A3, cache以上代碼基本體現了 dropout 的實現的四步流程。
含 dropout 的反向傳播計算定義如下:
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dA2 = np.multiply(dA2, D2)
dA2 = dA2 / keep_prob
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dA1 = np.multiply(dA1, D1)
dA1 = dA1 / keep_prob
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients 在定義反向傳播計算函數時,我們必須丟棄和執行前向傳播時一樣的神經元。
最后帶有 dropout 的分類效果如下所示:
所以,總結而言,dropout 就是在正常的神經網絡基礎上給每一層的每一個神經元加了一道概率流程來隨機丟棄某些神經元以達到防止過擬合的目的。
本文來自《自興動腦人工智能》項目部:凱文。
-
人工智能
+關注
關注
1792文章
47436瀏覽量
238981 -
機器學習
+關注
關注
66文章
8425瀏覽量
132772 -
深度學習
+關注
關注
73文章
5508瀏覽量
121295
發布評論請先 登錄
相關推薦
NPU在深度學習中的應用
FPGA加速深度學習模型的案例
AI大模型與深度學習的關系
FPGA做深度學習能走多遠?
深度學習模型中的過擬合與正則化
深度學習中的時間序列分類方法
深度學習與nlp的區別在哪
深度神經網絡的設計方法
深度學習的模型優化與調試方法
深度學習與傳統機器學習的對比
深度解析深度學習下的語義SLAM




 【連載】深度學習筆記5:正則化與dropout
【連載】深度學習筆記5:正則化與dropout











評論