提及機器學習,很多人會推薦斯坦福CSS 229。本文便對該課程做了系統的整理。包括監督學習、非監督學習以及深度學習。可謂是是學習ML的“掌上備忘錄”。
斯坦福CS229—機器學習:
監督學習
非監督學習
深度學習
機器學習備忘錄——監督學習
監督學習簡介
給定一組與輸出{y(1),...,y(m)}相關聯的數據點{x(1),...,x(m)},我們希望構建一個能夠根據x值預測y值的分類器。
預測類型—下表歸納了不同類型的預測模型

模型類型—下表歸納了不同的模型

符號和概念
假設—記一個假設為hθ,且是我們選擇的一個模型。給定一組輸入數據x(i),則模型預測輸出為hθ(x(i))。
損失函數—一個損失函數可表示為L:(z,y)∈R×Y?L(z,y)∈R,它將與實際數據值y對應的預測值z作為輸入,并輸出它們之間的差異。常見的損失函數歸納如下:

成本函數—成本函數J通常用于評估模型的性能。用損失函數L定義如下:
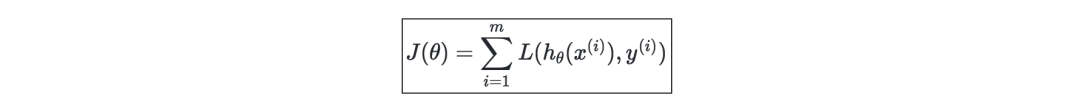
梯度下降—若學習率表示為α∈R,則用學習率和成本函數J來定義梯度下降的更新規則,可表示為如下公式:
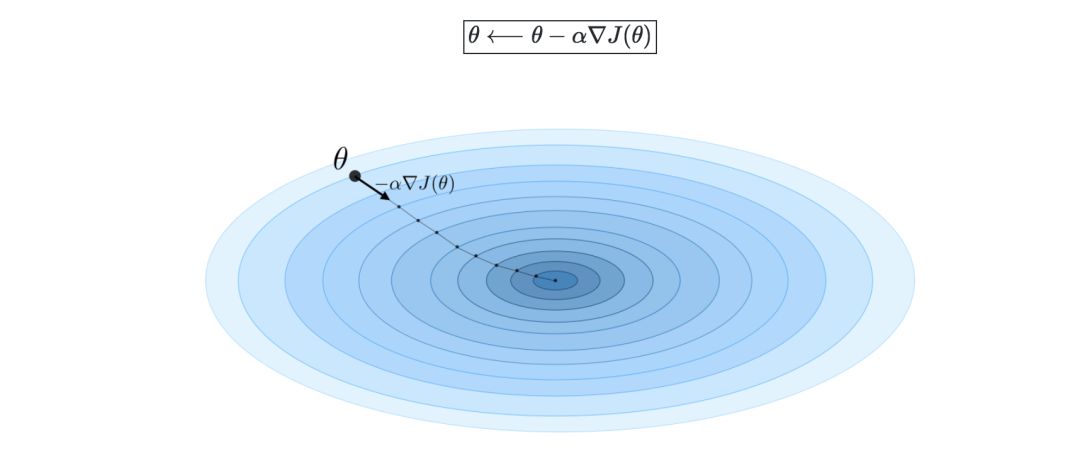
隨機梯度下降法(SGD)是根據每個訓練樣本對參數進行更新,批量梯度下降法是對一批訓練樣本進行更新
似然—一個模型的似然(給定參數L(θ)),是通過將其最大化來尋找最優參數θ。在實際過程中,我們一般采用對數似然?(θ)=log(L(θ)),因其優化操作較為容易。可表示如下:
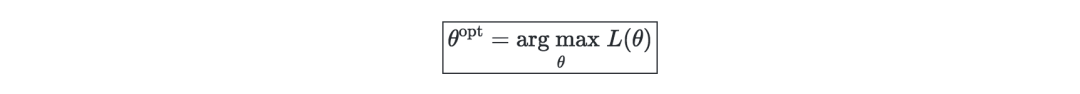
牛頓迭代法—是一種數值方法,用于找到一個θ,使?′(θ)=0成立。其更新規則如下:
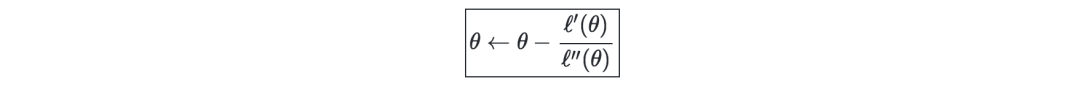
線性模型
線性回歸
我們假設y|x;θ~N(μ,σ2)。
正規方程(Normal Equation)—記X為矩陣,能使成本函數最小化的θ的值是一個封閉的解:

最小均方算法(LMS)—記α為學習率,對一個包含m個數據點的訓練集的LMS算法的更新規則(也叫Widrow-Hoff學習規則),如下所示:
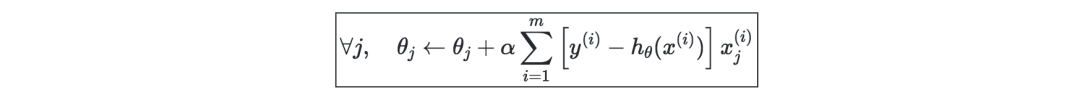
局部加權回歸(LWR)—是線性回歸的一種變體,它將每個訓練樣本的成本函數加權為w(i)(x),用參數τ∈R可定義為:

分類和邏輯回歸
Sigmoid函數—即S型函數,可定義為:

邏輯回歸—一般用于處理二分類問題。假設y|x;θ~Bernoulli(?),可有如下形式:

Softmax回歸—是邏輯回歸的推廣,一般用于處理多分類問題,可表示為:

廣義線性模型
指數族(Exponential family)—若一類分布可以用一個自然參數來表示,那么這類分布可以叫做指數族,也稱作正則參數或連結函數,如下所示:
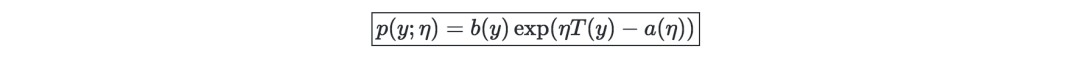
下表是常見的一些指數分布:
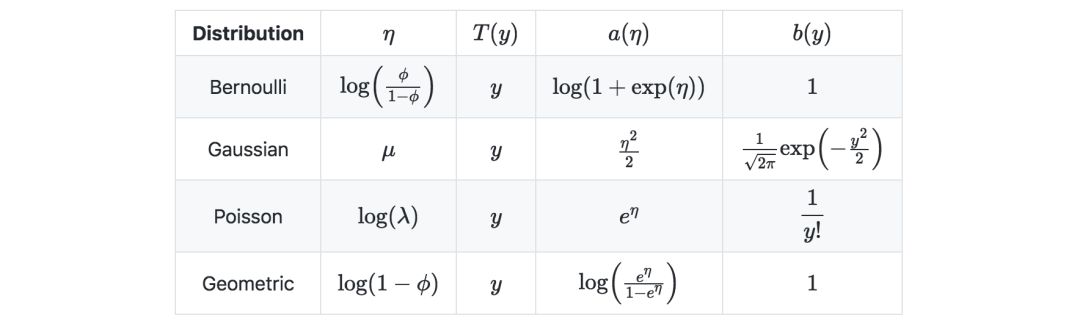
廣義線性模型的假設—廣義線性模型旨在預測一個隨機變量y,作為x∈Rn+1的函數,并且以來于以下3個假設:
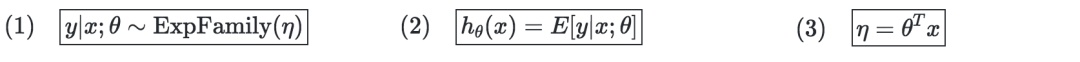
支持向量機
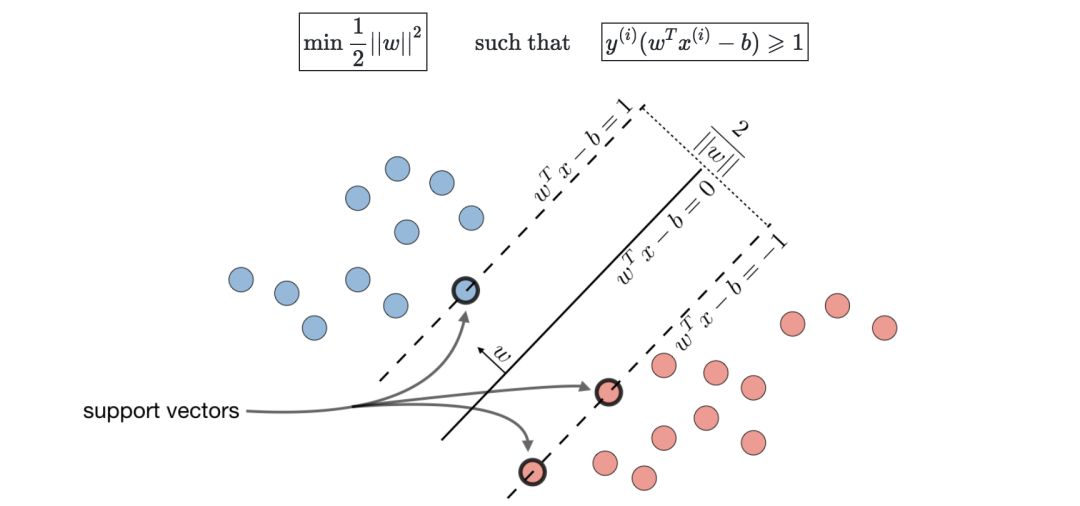
通俗來講,支持向量機就是要找到一個超平面,對樣本進行分割。
最優邊緣分類器—以h表示,可定義為:

其中,(w,b)∈Rn×R是如下最優問題的解:
Hinge損失—用于SVM的設置,定義如下:
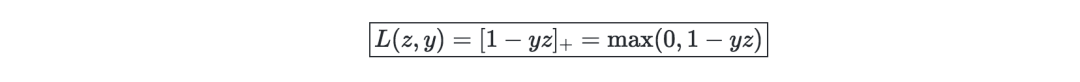
核(Kernel)—給定一個特征映射?,核可以表示為:

在實際問題當中,高斯核是較為常用的。
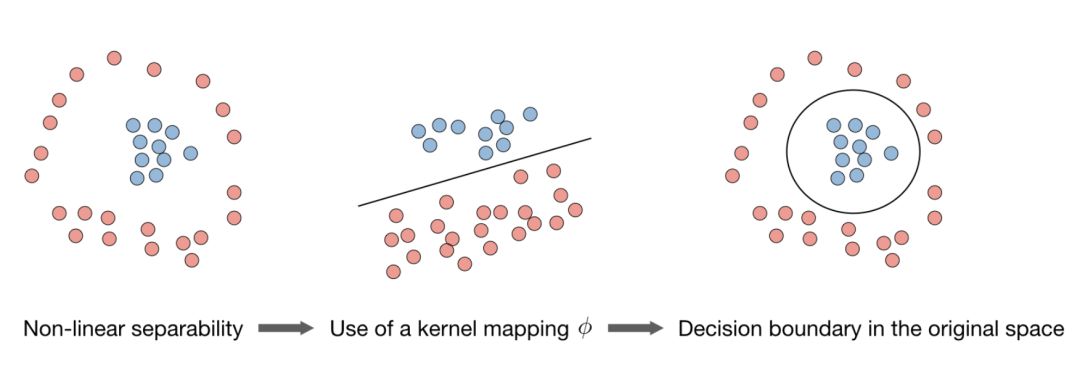
我們一般不需要知道XX的顯式映射,只需要知道K(x,z)的值即可
拉格朗日—我們定義拉格朗日L(w,b)為:
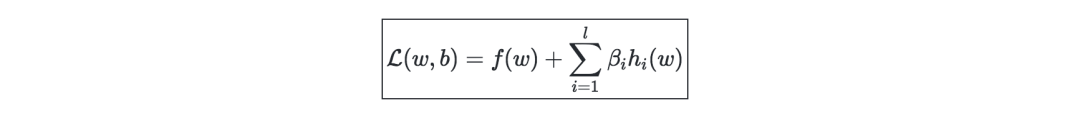
生成學習
生成模型首先嘗試通過估計P(x|y)來了解數據是如何生成的,而后我們可以用貝葉斯規則來估計P(y|x)。
高斯判別分析
Setting—高斯判別分析假設存在y、x|y=0和x|y=1,滿足:

估計—下表總結了最大化似然時的估計:

樸素貝葉斯
假設—樸素貝葉斯模型假設每個數據點的特征都是獨立的:
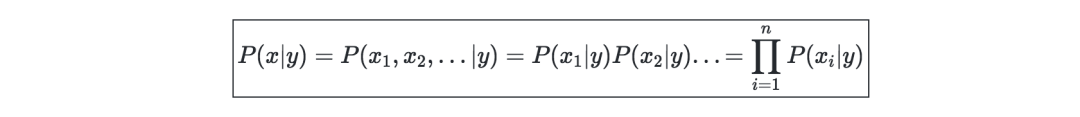
解決方案—當k∈{0,1},l∈[[1,L]]時,最大化對數似然給出了如下解決方案:
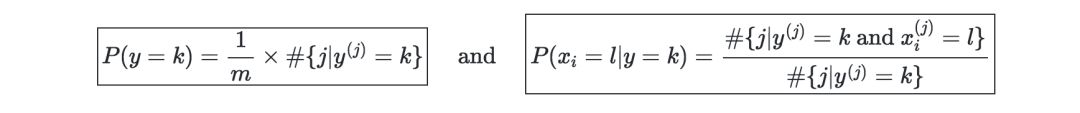
基于樹方法和集成方法
即可用于回歸,又可用于分類的方法。
決策樹—分類和回歸樹(CART),非常具有可解釋性特征。
Boosting—其思想就是結合多個弱學習器,形成一個較強的學習器。
隨機森林—在樣本和所使用的特征上采用Bootstrap,與決策樹不同的是,其可解釋性較弱。
其它非參數方法
KNN—即k近鄰,數據點的響應由其k個“鄰居”的性質決定。
學習理論(Learning Theory)
Union Bound—令A1,...,Ak為k個事件,則有:

Hoeffding inequality—刻畫的是某個事件的真實概率與m各不同的Bernoulli試驗中觀察到的頻率之間的差異。

訓練誤差—給定一個分類器h,我們將訓練誤差定義為error??(h),也被稱作經驗風險或經驗誤差,如下所示:
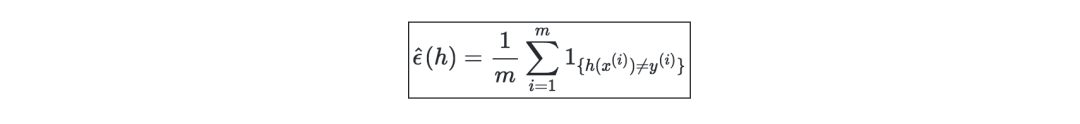
Probably Approximately Correct—即PAC,是一個框架,在此框架下,許多關于學習理論的結果都得到了證明,并且有以下一組假設:
訓練和測試集遵循相同的分布
訓練樣本是獨立繪制的
除上述學習理論之外,還有Shattering、上限定理、VC維、Theorem (Vapnik)等概念,讀者若感興趣,可由文末鏈接進入原文做進一步了解。
機器學習備忘錄——非監督學習
非監督學習簡介
無監督學習旨在無標記數據中發現規律。
詹森不等式—令f為凸函數、X為一個隨機變量。將會有如下不等式:

聚類
最大期望算法(EM)
隱變量—是指使估計問題難以解決的隱藏/未觀察到的變量,通常表示為z。下表是涉及到隱變量的常用設置:

算法—EM算法通過重復構建似然下界(E-step)并優化該下界(M-step)來給出通過MLE估計參數θ的有效方法,如下:

k-means聚類
令c(i)表示為數據點i的類,μj為類j的中心。
算法—在隨機初始化聚類質心μ1,μ2,...,μk∈Rn之后,k均值算法重復以下步驟直到收斂:
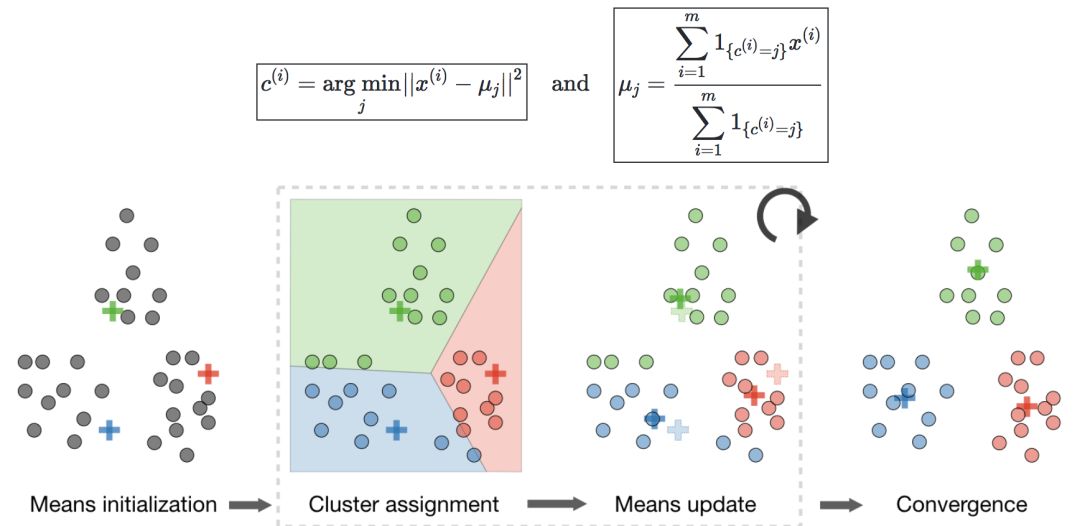
失真函數(distortion function)—為了查看算法是否收斂,定義如下的失真函數:

分層聚類
算法—它是一種聚類算法,采用聚合分層方法,以連續方式構建嵌套的聚類。
類型—為了優化不同的目標函數,有不同種類的層次聚類算法,如下表所示:

聚類評估指標
在無監督的學習環境中,通常很難評估模型的性能,因為沒有像監督學習環境中那樣的ground-truth標簽。
輪廓系數—記a為一個樣本和同一個類中其它點距離的平均,b為一個樣本與它最近的類中所有點的距離的平均。一個樣本的輪廓系數可定義為:
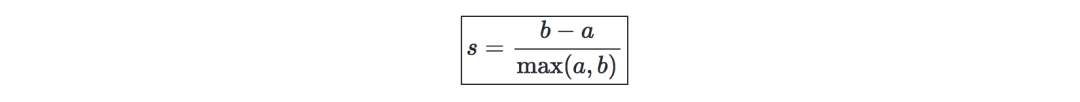
Calinski-Harabaz指數—記k為類的數量,XX和XX是類間、類內矩陣的dispersion矩陣分別表示為:

Calinski-Harabaz指數s(k)表明了聚類模型對聚類的定義的好壞,得分越高,聚類就越密集,分離得也越好。定義如下:

降維
主成分分析
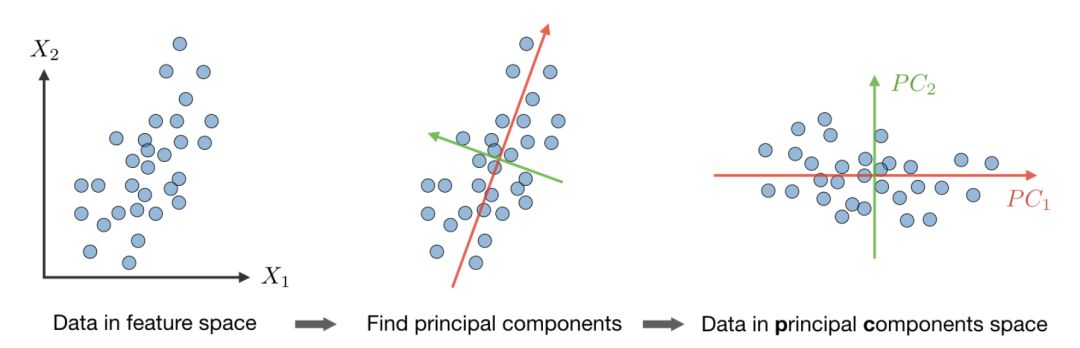
主成分分析是一種統計方法。通過正交變換將一組可能存在相關性的變量轉換為一組線性不相關的變量,轉換后的這組變量叫主成分。
特征值、特征向量—給定一個矩陣A∈Rn×n,如果存在一個向量z∈Rn?{0},那么λ就叫做A的特征值,而z稱為特征向量:
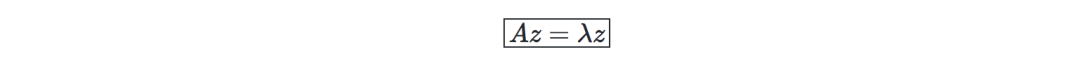
普定理(Spectral theorem)—令A∈Rn×n。若A是對稱的,那么A可以通過實際正交矩陣U∈Rn×n對角化。記Λ=diag(λ1,...,λn),我們有:

算法—主成分分析(PCA)過程是一種降維技術,通過使數據的方差最大化,在k維上投影數據,方法如下:
第一步:將數據標準化,使其均值為0,標準差為1。
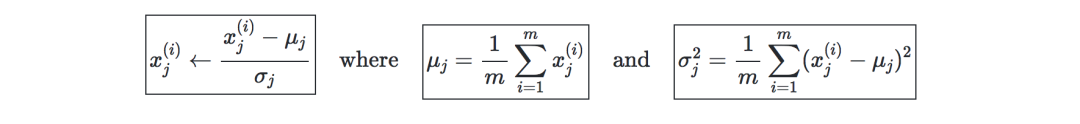
第二步:計算
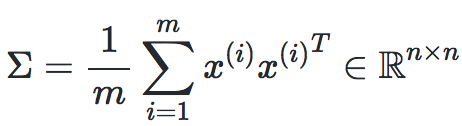
第三步:計算Σ的k個正交主特征向量,即k個最大特征值的正交特征向量。
第四步:在spanR(u1,...,uk)上投射數據。
這個過程使所有k維空間的方差最大化。
獨立分量分析
這是一種尋找潛在生成源的技術。
假設—我們假設數據x是通過混合和非奇異矩陣A,由n維源向量s=(s1,...,sn)生成的(其中,si是獨立的隨機變量),那么:
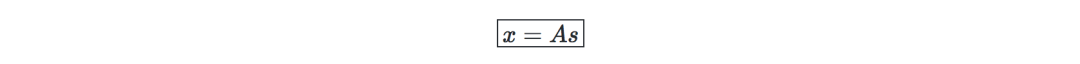
目標是找到混合矩陣W=A?1
Bell和Sejnowski的ICA算法—該算法通過以下步驟找到解混矩陣W:
將x=As=W?1sx=As=W?1s的概率表示為:
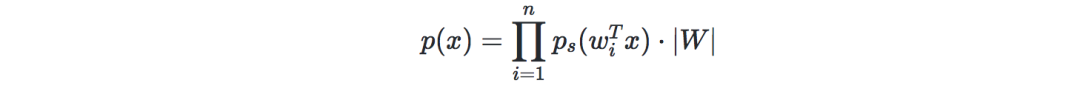
記g為sigmoid函數,給定我們的訓練數據{x(i),i∈[[1,m]]},則對數似然可表示為:
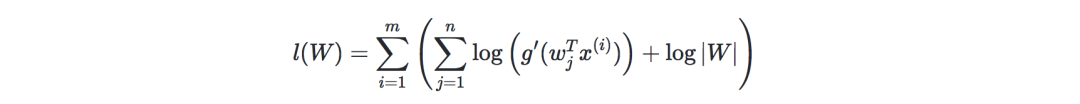
因此,隨機梯度上升學習規則是對于每個訓練樣本x(i),我們更新W如下:

機器學習備忘錄——深度學習
神經網絡是一類用層構建的模型。常用的神經網絡類型包括卷積神經網絡和遞歸神經網絡。
結構—關于神經網絡架構的描述如下圖所示:

記i為網絡中的第i層,j為一個層中第j個隱含單元,這有:
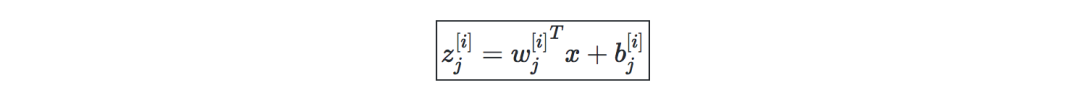
激活函數—在隱含單元的末端使用激活函數向模型引入非線性復雜性。以下是最常見的幾種:

交叉熵損失-在神經網絡中,交叉熵損失L(z,y)是常用的,定義如下:

學習率—通常被記作α或η,可表明在哪一步權重得到了更新。這可以被修正或自適應的改變。目前最流行的方法是Adam,這是一種適應學習率的方法。
反向傳播—是一種通過考慮實際輸出和期望輸出來更新神經網絡權重的方法。關于權重w的導數是用鏈式法則計算的,它的形式如下:
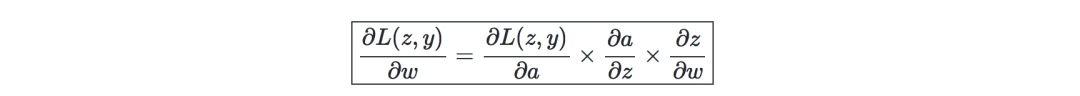
因此,權重更新如下:
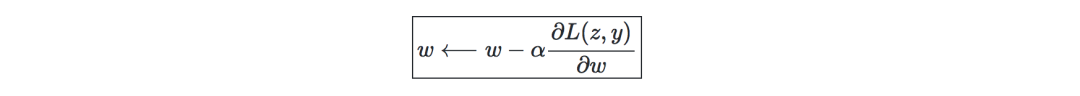
更新權重—在神經網絡中,權重的更新方式如下:
第一步:對訓練數據取一個batch;
第二步:進行正向傳播以獲得相應的損失;
第三步:反向傳播損失,得到梯度;
第四步:使用梯度更新網絡的權重。
Dropout—是一種通過在神經網絡中刪除單元來防止過度擬合訓練數據的技術。
卷積神經網絡
超參數—在卷積神經網絡中,修正了以下超參數:

層的類型—在卷積神經網絡中,我們可能遇到以下類型的層:

卷積層要求—記W為輸入量大小,F為卷積層神經元大小,P是zero padding的數量,那么在給定體積(volumn)內的神經元數量N是這樣的:
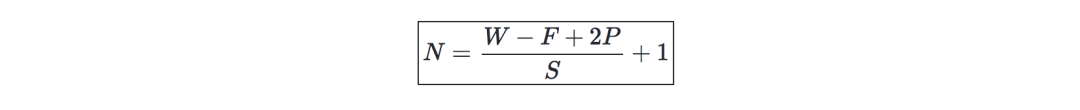
Batch歸一化—記γ,β為我們想要更正的batch的均值和方差,則:
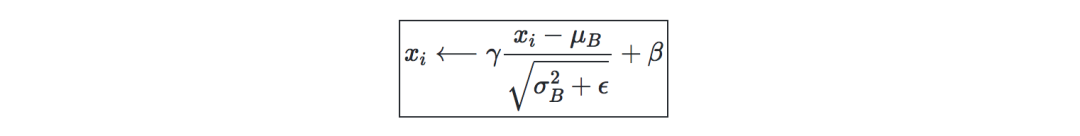
它通常是在完全連接/卷積層和非線性層之前完成的,目的是提高學習率并減少對初始化的強烈依賴。
遞歸神經網絡
gate的類型—以下是在典型遞歸神經網絡中存在的不同類型的gate:

LSTM—該網絡是一種RNN模型,它通過添加“forget” gates來避免梯度消失問題。
強化學習與控制
強化學習的目標是讓智能體學會如何在環境中進化。
馬爾科夫決策過程—即MDP,是一個五元組(S,A,{Psa},γ,R),其中:
S是一組狀態;
A是一組行為;
{Psa}是s∈S和a∈A的狀態轉換率;
γ∈[0,1]是discount系數;
R:S×A?R或R:S?R是算法要最大化的獎勵函數
加粗:策略—是一個函數π:S?A,是將狀態映射到行為中。
加粗:Value Function—給定一個策略π和狀態s,可定義value functionVπ
為:

貝爾曼方程—最優貝爾曼方程刻畫了最優策略π的value function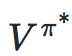 :
:

Value迭代算法—主要分為兩個步驟:
初始化value:
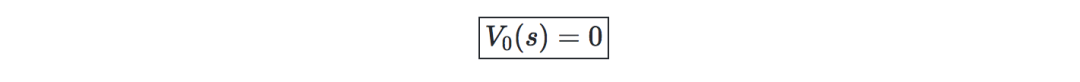
基于之前的value進行迭代:
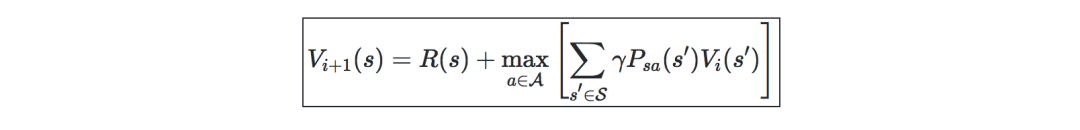
最大似然估計—狀態轉移概率的最大似然估計如下:

Q-Learning—是Q一種無模型估計,公式如下:
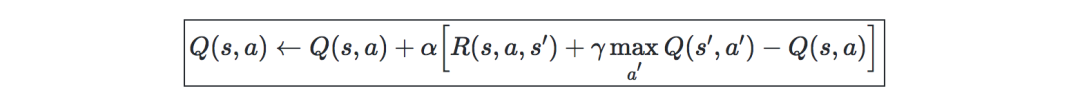
-
分類器
+關注
關注
0文章
152瀏覽量
13206 -
機器學習
+關注
關注
66文章
8430瀏覽量
132856 -
深度學習
+關注
關注
73文章
5511瀏覽量
121355
原文標題:【斯坦福CS229】一文橫掃機器學習要點:監督學習、無監督學習、深度學習
文章出處:【微信號:AI_era,微信公眾號:新智元】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦




 斯坦福CSS 229系統的整理,學習ML的“掌上備忘錄
斯坦福CSS 229系統的整理,學習ML的“掌上備忘錄












評論