摘要:
設計了發射線圈平面纏繞和發射線圈豎直纏繞這兩種不同的耦合結構,通過分析選擇了一種傳輸功率大的耦合機構,并研究了這種耦合機構在接收線圈沿軌道運動時非接觸電能傳輸的平穩性狀況。借用ANSYS有限元仿真工具,得到這兩種耦合結構耦合線圈的自感及互感,再仿真這種耦合機構沿軌道相對運動時傳輸功率的變化情況。實驗中制作了這兩種耦合機構,最后選用了一種傳輸能力強的耦合機構,使其沿軌道水平運動,結果表明系統能夠保持良好的平穩性。
0 引言
感應耦合式非接觸電能傳輸(Inductive Contactless Power Transfer,ICPT)是一種電源與負載之間沒有直接的電氣接觸能量傳輸方式,不會產生電火花,避免了導線拖拽帶來的不便,減少了有線供電存在的安全隱患[1]。因此,ICPT在一些特殊的場合下有著廣泛的應用前景,比如應用在電動汽車的無線充電以及在一些起重運輸的設備上[2-4]。
針對ICPT的耦合機構,國內外許多研究機構對此進行專門的研究。以新西蘭BOY T教授為首的課題組提出了一種E型耦合結構,這種耦合結構的初次級線圈耦合緊密、效率高、傳輸功率大[5-6]。文獻[7]針對電動汽車無線充電,為使耦合機構提供一個較大的充電區域,設計了一種DLDD(Double Layer Double D-type)形式的耦合線圈。文獻[8]中又提出一種新型的耦合結構——H型結構,該機構具有效率高、橫向位移范圍大和質量輕等特點。以上文獻中均未對耦合機構沿軌道相對運動時,ICPT系統的平穩性進行研究。
本文利用ANSYS有限元軟件并設計了實驗,最后得出在耦合機構沿軌道相對運動時,ICPT系統能夠保持良好的平穩性的結論。
1 沿軌道相對運動的耦合結構
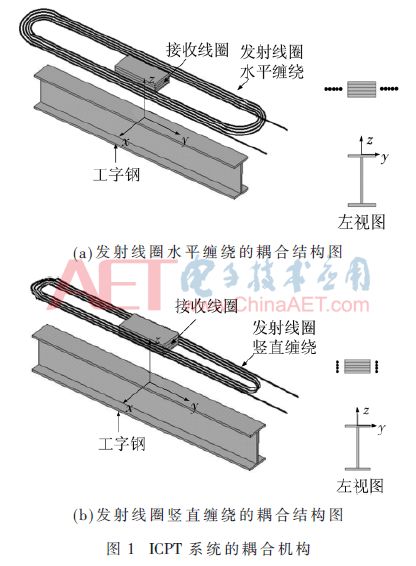
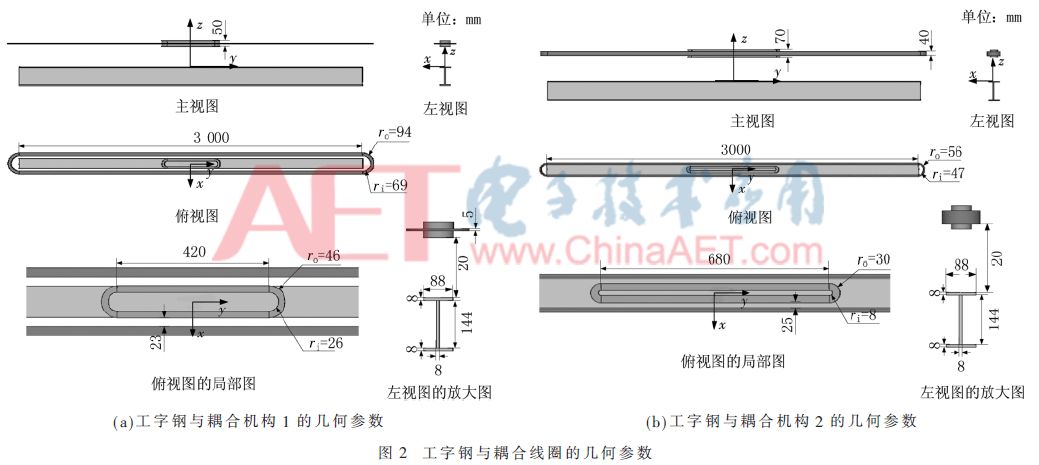
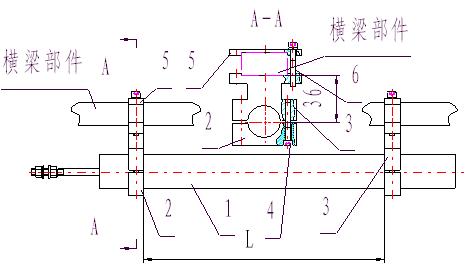
本文以起重運輸設備為背景,為了便于對比,設計并制作了兩種耦合結構沿軌道相對運動的ICPT系統,如圖1所示,在后文分別稱為耦合機構1和耦合機構2,它們的幾何參數如圖2所示。兩者主要區別是,耦合機構1的發射線圈是水平纏繞,而耦合機構2的發射線圈是豎直纏繞。其支撐框架均為木材和有機玻璃框架,發射線圈固定在起承重作用的工字鋼梁上,接收線圈與其他所有接收裝置沿工字鋼橫梁做水平直線運動。因而,發射線圈與接收線圈存在長距離的相對運動。
2 理論分析
2.1 耦合線圈參數的理論分析
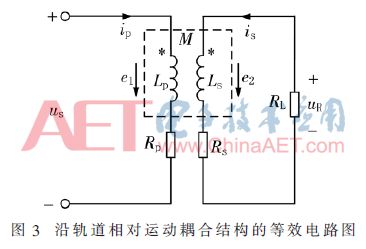
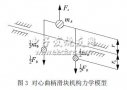
基于ANSYS有限元仿真得到的結果,通過ICPT系統的等效電路模型分析可得到耦合線圈的自感及互感。圖1中所表示的沿軌道相對運動耦合結構的等效電路圖如圖3所示。


式(2)是一個復數方程組,根據互感線圈二端口輸入、輸出能量守恒,可推出式(2)中只有3個實數方程線性無關。因此式(2)中Lp、Ls和M有唯一解。
2.2 非接觸電能傳輸系統的傳輸功率
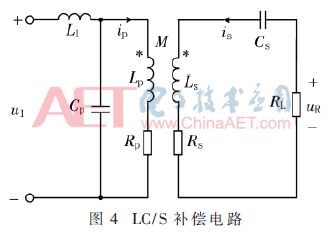
本文采用LC/S網絡補償方式,其補償電路圖如圖4所示,將接收端等效到發射端,再將發射端電路用諾頓電路等效,其等效電路圖如圖5所示,Zeq為接收端等效到發射端的等效阻抗。
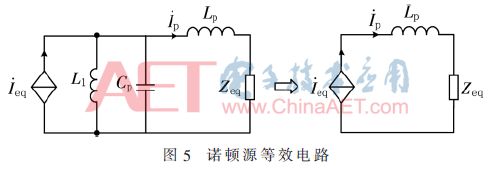
其諾頓等效源為:

將圖4中接收側回路用受控源回路等效,如圖6所示。
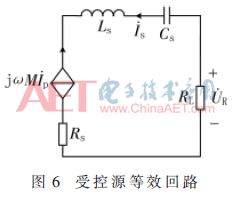
接收側回路滿足:
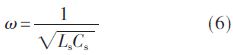
因此,ICPT系統的傳輸功率為:
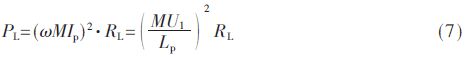
3 耦合機構的仿真結果
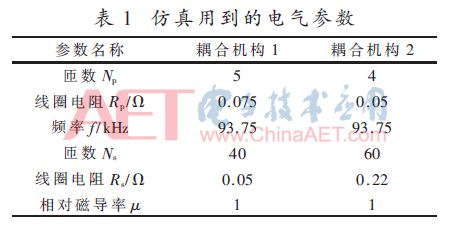
本文使用通用電磁場仿真工具ANSYS有限元軟件,對上述這兩種耦合機構進行仿真。設定耦合機構中發射線圈距工字鋼距離d=20 cm,電源電壓Us=351 V,負載電阻RL=68 Ω,仿真中所用到的電氣參數如表1所示。工字鋼相對磁導率μ為4 000,電阻率為20×10-8Ω/m。
3.1 兩種耦合機構傳輸能力的比較
利用耦合線圈與工字鋼結構對稱特點,采用其二分之一結構模型。借用ANSYS有限元仿真軟件,得到如圖7所示耦合線圈感應電動勢的實部,同理,還可得到耦合線圈感應電動勢的虛部及負載電壓。圖7是耦合機構1接收線圈處于中間的位置。

因此,通過ANSYS有限元仿真可得出發射線圈和接收線圈的感應電動勢及負載電壓。根據第2部分的理論推導,可得耦合機構線圈的自感和互感如表2所示。
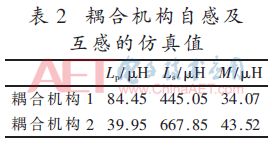
由表2可知,耦合機構1的M1/Lp1=0.4,耦合機構2的M2/Lp2=1.1,而系統的傳輸功率正比于M與Lp比值的平方,即耦合機構2比耦合機構1的傳輸能力強,因此,下面將對耦合機構2沿軌道相對運動進行ICPT的平穩性研究。
3.2 耦合機構2沿軌道相對運動
下面研究耦合機構2沿軌道相對運動時,ICPT功率的變化情況。分為以下3種情況:(1)接收線圈相對于發射線圈沿水平方向運動;(2)接收線圈相對于發射線圈在豎直方向上有偏離;(3)接收線圈在發射線圈內前后側方向上有偏離。
為了消除系統的無功損耗,減小回路阻抗,需要在接收回路中串聯補償電容。耦合機構2中接收線圈的自感Ls2=667.848 μH,根據串聯諧振公式: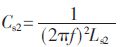 s2≈4.32 nF。由于串聯補償電容的影響,導致接收側回路中的交流電流i2的變化很大,這樣工字鋼會反過來影響耦合線圈的自感,因此根據Ls2=667.848 μH計算出來的串聯諧振電容Cs2≈4.32 nF并不是最佳的補償電容值。可從優化方法的思想,根據仿真尋找出串聯補償電容的最優值,其結果如表3所示。
s2≈4.32 nF。由于串聯補償電容的影響,導致接收側回路中的交流電流i2的變化很大,這樣工字鋼會反過來影響耦合線圈的自感,因此根據Ls2=667.848 μH計算出來的串聯諧振電容Cs2≈4.32 nF并不是最佳的補償電容值。可從優化方法的思想,根據仿真尋找出串聯補償電容的最優值,其結果如表3所示。
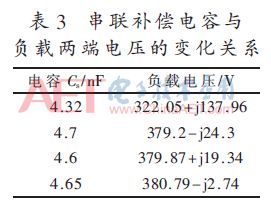
由表3可知,接收回路中串聯補償電容的大小近似為4.65 nF,而實驗中串聯補償電容選為4.7 nF,因此仿真中選用接收回路的串聯補償電容為4.7 nF。
3.2.1 接收線圈相對于發射線圈沿水平方向運動
下面仿真耦合機構2的接收線圈沿水平方向運動時ICPT系統的平穩性情況。記發射線圈的中心位置為原點O,以接收線圈在水平方向上的運動軌跡定為x軸,分別對接收線圈的中心位于x=±105 cm、±75 cm、±45 cm、±15 cm這8個位置仿真,得到耦合機構2系統的傳輸功率隨水平位置的變化曲線如圖8所示,其中系統的傳輸功率的相對變化量在2%之內。
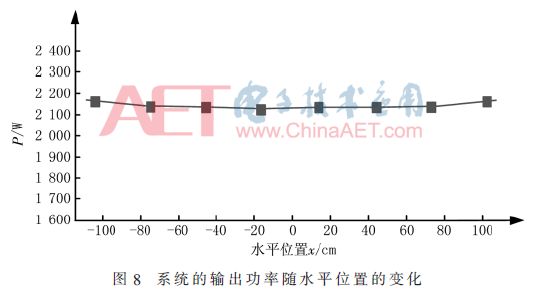
3.2.2 接收線圈相對發射線圈在豎直方向上有偏離
接收線圈相對于發射線圈在豎直方向上有偏離的情況下,仿真耦合機構2系統的傳輸功率的變化情況。其相對偏離量是在接收線圈的自身高度±10%內,圖9是其傳輸功率隨偏離量的變化曲線,其中傳輸功率相對于無偏離時最大的相對變化量均不大于5%。
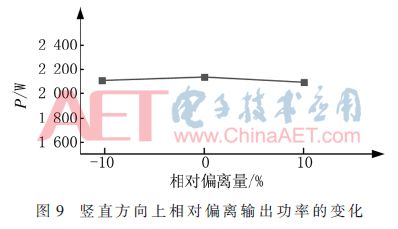
3.2.3 接收線圈在發射線圈內前后側方向上有偏離
接收線圈在發射線圈內前后側有偏離的情況下,仿真系統的傳輸功率的變化情況。其相對偏離量是耦合線圈之間空隙的±20%內,圖10是其傳輸功率隨偏離量的變化曲線。其中系統的傳輸功率相對于無偏離時的相對變化量均不大于2%。

從圖8~圖10的仿真結果可知,耦合機構2沿軌道相對運動時,ICPT系統傳輸功率的波動范圍均在5%之內,說明這種耦合機構在傳輸電能的過程中能夠保持良好的平穩性。
4 實驗結果
4.1 耦合線圈中自感和互感的測量
圖11是實驗中搭建的兩種耦合機構的實驗平臺,左圖是耦合機構1實驗裝置,右圖是耦合機構2實驗裝置。在接收線圈處于發射線圈的中間位置,實驗測得這兩種耦合機構的自感和互感如表4所示。
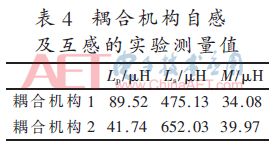
將表2中的仿真值與表4中的實驗值對比,根據誤差計算公式:誤差=

4.2 耦合機構2沿軌道水平運動時測互感的實驗
當接收線圈沿軌道水平運動時,利用PA2000mini功率測試儀對ICPT系統進行測試。按照3.2.1小節中8個位置的傳輸功率進行測量,得到的結果如圖12所示,其中傳輸功率的最大波動在6%之內。圖13是接收線圈運動到某一位置時的測量結果,圖中星號標記點處系統的輸出功率為2.073 kW。
實驗結果表明,由實驗測量到的數據與仿真數據存在一定的誤差,但數據相差不大,并且變化趨勢基本保持一致,主要原因是在仿真過程中,耦合結構的建模采用了簡化的模型。
5 結論
借用ANSYS電磁場仿真軟件分析了耦合機構沿軌道相對運動時,ICPT系統能夠保持良好的平穩性,并通過實驗驗證了該結論。通過理論分析和實驗分析發現,工字鋼對耦合線圈的自感確實存在一定的影響,使得在接收回路中串聯補償電容的理論計算值和實驗值存在一定的差異,而利用ANSYS電磁場仿真軟件能夠很好地解決這一問題。
-
耦合
+關注
關注
13文章
582瀏覽量
100888 -
等效電路
+關注
關注
6文章
292瀏覽量
32773
原文標題:【學術論文】耦合機構沿軌道相對運動時系統的平穩性研究
文章出處:【微信號:ChinaAET,微信公眾號:電子技術應用ChinaAET】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
相關推薦
如何保持良好的工作體位?
【連載筆記】信號完整性-串擾和軌道塌陷
一種并聯諧振型ICPT電路頻率穩定性控制方法
衛星軌道運動MATLAB仿真
近圓軌道下航天器相對運動的滑模控制(通過MATLAB驗證)




 耦合機構沿軌道相對運動時,ICPT系統能夠保持良好的平穩性
耦合機構沿軌道相對運動時,ICPT系統能夠保持良好的平穩性












評論