謝昆諾夫(S.A. Schelkunoff)是國(guó)際知名的電磁理論科學(xué)家。從1934年解決同軸線內(nèi)電磁場(chǎng)結(jié)構(gòu)開(kāi)始,他在后來(lái)的三十年內(nèi),在工程電磁場(chǎng)、天線理論、波導(dǎo)理論等方面發(fā)表了數(shù)十篇論文和幾本書,提出了許多定理、原理、概念、方法(它們之中有許多早已寫人大學(xué)教材中),作出了重要的貢獻(xiàn)。他使應(yīng)用數(shù)學(xué)煥發(fā)出光采,許多工作帶有奠基性質(zhì)。就經(jīng)典電動(dòng)力學(xué)方法(即量子理論以外領(lǐng)域)而言,可以把他比作二十世紀(jì)的麥克斯韋。眾所周知,電磁波的波導(dǎo)在微波技術(shù)中有廣泛應(yīng)用,也是當(dāng)前光波導(dǎo)光纖的前驅(qū),因而介紹這方面的歷史是有意義的。
一
1897年1月27日,謝昆諾夫生于俄國(guó)薩馬拉,后隨家庭移居美國(guó)。1923年(26歲時(shí))在華盛頓州立學(xué)院獲碩士學(xué)位后,即加人西屋公司工作,兩年后轉(zhuǎn)人貝爾研究所。1928年,他在哥倫比亞大學(xué)獲博士學(xué)位。以后,長(zhǎng)期在貝爾研究所擔(dān)任高級(jí)科學(xué)家。
謝昆諾夫開(kāi)始從事研究工作的時(shí)期,正處在電子學(xué)從短波技術(shù)向超高頻、微波技術(shù)發(fā)展的時(shí)代。筆者在前文[1]中,曾談過(guò)兩位英國(guó)物理學(xué)家(O. Heaviside和J.J. Thomson)于1893年就波導(dǎo)的可實(shí)現(xiàn)性發(fā)表尖銳對(duì)立的意見(jiàn)的情形。顯然,只有實(shí)驗(yàn)上的完全成功,才能對(duì)這一爭(zhēng)論的是非作出最后的判斷。在貝爾研究所,一方面有以G.C. Southworth為首的小組從事建立波導(dǎo)線路的實(shí)驗(yàn)研究,同時(shí)又有以J.R. Carson為首的小組進(jìn)行波導(dǎo)理論的數(shù)學(xué)分析工作。謝昆諾夫參加了后者。1936年,Carson,Mead和謝昆諾夫發(fā)表了題為《高頻波導(dǎo)數(shù)學(xué)理論》的論文,該論文反映的最重要的成果是導(dǎo)出了圓波導(dǎo)的嚴(yán)格的超越方程(即CMS方程[2,3])。論文中假定壁電導(dǎo)率為有限,同時(shí)作混合模(hybrid modes)分析。論文所導(dǎo)出的CMS方程實(shí)質(zhì)是本征值方程,具有重要意義和實(shí)用價(jià)值。正是這篇論文命名了HE和EH模。CMS方程是針對(duì)金屬壁波導(dǎo)提出的,但經(jīng)過(guò)J.A. Stratton[4]的普遍化討論后,也適用于近代出現(xiàn)的光纖。因此,正是從1936年開(kāi)始,謝昆諾夫和比他年長(zhǎng)的貝爾研究所的研究數(shù)學(xué)家(research mathematician)J.R. Carson一起,作出了極有價(jià)值的貢獻(xiàn)。實(shí)際上,1934年謝昆諾夫在獨(dú)立發(fā)表關(guān)于同軸線這一雙導(dǎo)體導(dǎo)波體系的理論時(shí)[5],就一直在思考如何從數(shù)學(xué)上來(lái)處理單導(dǎo)體導(dǎo)波體系的波導(dǎo)問(wèn)題。
1937年,謝昆諾夫發(fā)表了題為《平面電磁波傳輸理論》的論文[6],單獨(dú)一人作出了非常重要的貢獻(xiàn)。在這篇論文中,他率先把阻抗概念用于處理電磁場(chǎng)問(wèn)題;他提出了無(wú)耗波導(dǎo)截止頻率的定義;他首創(chuàng)計(jì)算衰減常數(shù)的功率損耗法(power loss method),這在V.M. Papadopoulos[7]1954年論文發(fā)表之前是唯一能作數(shù)值計(jì)算的方法;他最先采用分布參數(shù)等效電路以分析自由空間的和導(dǎo)波的傳播,在這過(guò)程中,他利用矢量勢(shì)(vector potential)A作為工具。實(shí)際上,他的這些研究成果早已成為電磁場(chǎng)理論、波導(dǎo)理論教科書的基本內(nèi)容。
三十年代末至五十年代初,是謝昆諾夫的多產(chǎn)時(shí)期,其間屢有佳作。例如,1938年他研究了微小失圓管子中的導(dǎo)波[8];1944年他對(duì)無(wú)限長(zhǎng)矩形波導(dǎo)中的TE10(H10)模的純行波,定義了一組(三個(gè))特性阻抗[9];1952年他提出“廣義電報(bào)員方程”[10],這是研究圓波導(dǎo)中TE01(H01)模傳輸?shù)挠辛ぞ撸?955年以后人們用它解決了許多問(wèn)題(實(shí)際上,正是謝昆諾夫最先指出圓波導(dǎo)中存在頻率越高衰減越小的模式,即H01模)。這些都是對(duì)波導(dǎo)理論直接作出的貢獻(xiàn)。同波導(dǎo)理論間接有關(guān)的工作也很多,例如,1948年他討論了由均勻媒質(zhì)等效空間網(wǎng)絡(luò)導(dǎo)出麥克斯韋方程組[11];1951年提出電磁場(chǎng)等價(jià)定理(field equivalence theorems)[12],它可用來(lái)解決波導(dǎo)的小孔激發(fā)理論問(wèn)題;1952年,他由半無(wú)限導(dǎo)體圓錐的分析,解決了半無(wú)限長(zhǎng)線電流產(chǎn)生的場(chǎng)分布[13];1955年,他通過(guò)正交函數(shù)展開(kāi),將麥克斯韋方程組轉(zhuǎn)換為具體問(wèn)題的耦合波方程組[14]等等。
二
指出下述的年代方面的巧合是非常有趣的:謝昆諾夫出生的那一年(1897),恰恰是瑞利第一次全面討論波導(dǎo)的那年[15,16],從那時(shí)到波導(dǎo)實(shí)驗(yàn)成功(1936)[17]恰為39年;而謝昆諾夫正是在39歲時(shí),參加Carson領(lǐng)導(dǎo)的小組完成了對(duì)圓波導(dǎo)特征方程的推導(dǎo)工作[2]。
基于一種科學(xué)思維上的敏感或直覺(jué),謝昆諾夫?qū)ζ矫骐姶挪ǎㄒ环N非常基本的波)的性質(zhì)進(jìn)行了深人的研究。他指出[6],平面波可在理想導(dǎo)電壁金屬管子(圖1)中存在,但是近似平面的,等相面在邊界上畸變。
圖1、任意截面規(guī)則波導(dǎo)
從單色簡(jiǎn)諧波條件下的麥克斯韋方程出發(fā),在橫磁(TM)波和Hz=0的假定下,可以寫出標(biāo)量Ex,Ey,Ez,和Hx,Hy,Hz之間的關(guān)系式;又假定某個(gè)電位函數(shù)U(表示在給定點(diǎn)與無(wú)限遠(yuǎn)之間沿著等相面上一條路徑的電動(dòng)勢(shì)作用),從而寫出
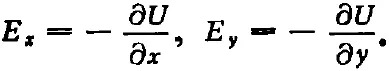
此外,引入矢量勢(shì)函數(shù)A(它的旋度是磁場(chǎng)強(qiáng)度矢量H),取A為z向矢量(A=Aziz,iz為z向單位矢),則得
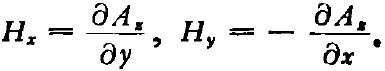
聯(lián)立以上三方面的關(guān)系式,可得
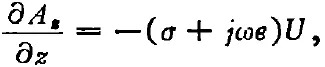
式中σ,
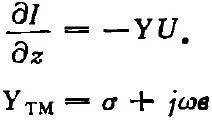
作為橫磁波傳輸?shù)刃榉植紖?shù)電路時(shí)的并聯(lián)導(dǎo)納.這樣,謝昆諾夫開(kāi)始在用等效電路描述波動(dòng)過(guò)程方面取得突破。
由麥克斯韋方程及上述關(guān)系式,可得
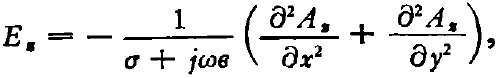
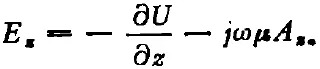
把(1)式代入(4)式,得
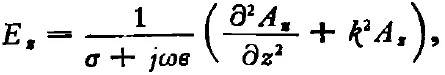
式中
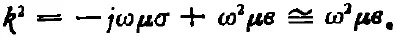
對(duì)比(3),(5)兩式,得
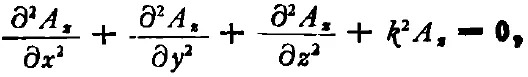
即
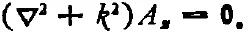
這是無(wú)源空間的齊次Helmholtz方程,說(shuō)明Az(或說(shuō)矢量A)是波方程的解。令
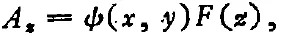
式中函數(shù)ψ表示場(chǎng)振幅在等相面上的分布;代入(5)式,得
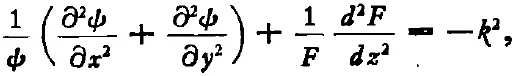
式中左邊第一項(xiàng)與z無(wú)關(guān),可令
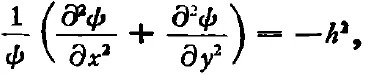
式中h與(x,y,z)及ψ無(wú)關(guān)。由于ψ是實(shí)數(shù),故h也是實(shí)數(shù)。又因F(z)與(x,y)無(wú)關(guān),故可取
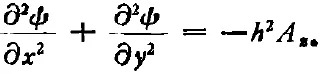
將(7)式帶入(3)式后,得
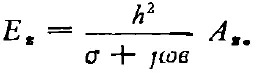
將(8)式與(4)式聯(lián)立,得
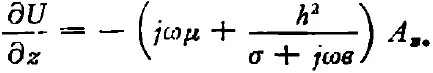
對(duì)比均勻傳輸線理論中的公式:
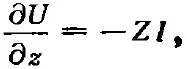
可取
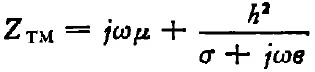
作為橫磁波傳輸分布等效電路的串聯(lián)阻抗,現(xiàn)在可用圖2來(lái)描寫TM波的波動(dòng)過(guò)程,并由(2)式和(10)式來(lái)決定元件的值:
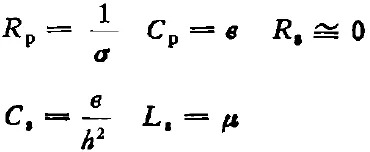
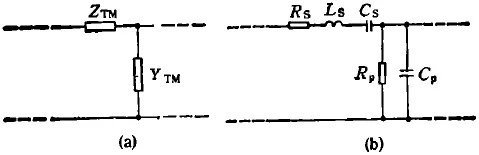
圖2、規(guī)則柱波導(dǎo)的TM波等效電路
當(dāng)然,參照濾波器理論還可求傳播常數(shù)、特性阻抗和截止頻率的表達(dá)式。
謝昆諾夫的上述處理不僅在理論上優(yōu)美、自洽,而且在工程計(jì)算上很方便。例如,對(duì)于圓波導(dǎo)和TM01模,有
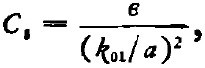
式中k01為Bessel函數(shù)J0(x)=0的第一根,a為波導(dǎo)內(nèi)半徑。
三
波導(dǎo)實(shí)驗(yàn)成功后最初幾年,人們吃不準(zhǔn)該怎樣看待它。問(wèn)題是能否把它看成傳輸線?能否計(jì)算它的阻抗和反射?正是謝昆諾夫及時(shí)解決了這些問(wèn)題。1937年,他首先提出了波導(dǎo)的波阻抗的定義。1944年,他又提出了特性阻抗的定義。他的分析主要針對(duì)矩形波導(dǎo)(圖3)。
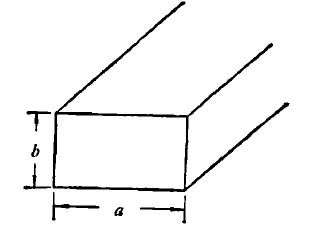
圖3、矩形波導(dǎo)
其中的橫向電場(chǎng)與橫向磁場(chǎng)的關(guān)系,對(duì)TE模為:
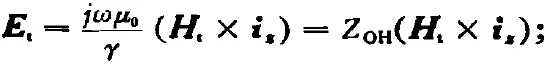
對(duì)理想導(dǎo)電壁波導(dǎo)主模(H10模),可證明
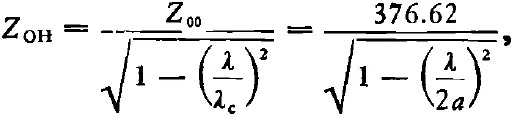
式中λ是工作波長(zhǎng),λc是截止波長(zhǎng),Z00是自由空間波阻抗。波導(dǎo)波阻抗是有用的概念,但卻無(wú)法解釋兩段波導(dǎo)(a一樣,b不同)相聯(lián)后有反射發(fā)生的事實(shí)。
三十年代末到四十年代初的微波測(cè)量實(shí)踐,證明關(guān)于行波、駐波、反射、圓圖等傳輸線概念、方法均可用于波導(dǎo)。因而為了應(yīng)用傳輸線理論就必須在單導(dǎo)體的波導(dǎo)情況下給出電壓和電流的定義。謝昆諾夫最早做了這個(gè)工作[9]。對(duì)矩形波導(dǎo)主模,他定義
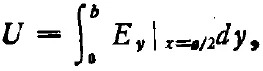
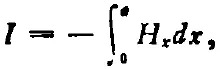
這樣他導(dǎo)出了一組(三個(gè))特性阻抗:
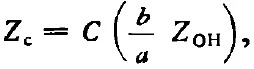
式中常數(shù)C可以是π|2,2,π2|8,因而特性阻抗失去了唯一性。由于表達(dá)式包含了b,因而解決了矛盾。
這是一個(gè)貢獻(xiàn),但謝昆諾夫自己也認(rèn)為這種處理不太自然。對(duì)這個(gè)問(wèn)題,幾十年來(lái)發(fā)生許多爭(zhēng)論[18-20],我們認(rèn)為D.M Kerns[19]的見(jiàn)解比較正確、全面;他認(rèn)為,由線積分定義電壓沒(méi)有普遍價(jià)值,因?yàn)椴⒎窃谝磺星闆r下均能知道波導(dǎo)內(nèi)的場(chǎng)圖。其次,“ 一根波導(dǎo)的特性阻抗”的說(shuō)法沒(méi)有意義,因?yàn)椴▽?dǎo)內(nèi)有多模,每個(gè)模式都有自己的波阻抗值。但Kerns并不完全否定謝昆諾夫的方法在分析波導(dǎo)中不連續(xù)性問(wèn)題時(shí)有價(jià)值,因而與完全否定的觀點(diǎn)[20]不同。
目前采用的定義波導(dǎo)電壓和電流的方法是以基準(zhǔn)場(chǎng)(basis fields)理論為基礎(chǔ)。這一較好方法是S.Silver[21]最先提出的。它把波導(dǎo)內(nèi)橫向場(chǎng)寫為
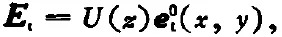
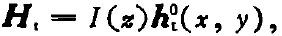
Silver把式中的U,I分別稱為模式電壓、電流參數(shù)。今天,我們稱
但是,謝昆諾夫的方法直到今天仍在使用著。例如,1983年發(fā)表的關(guān)于雙脊波導(dǎo)的論文山[22],對(duì)電壓的定義為
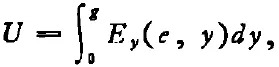
這顯然仍是謝昆諾夫方式。因此,向人們介紹這位在本世紀(jì)三十至六十年代非常活躍的電磁理論科學(xué)家的成就是十分必要的。
本文只是簡(jiǎn)介謝昆諾夫在波導(dǎo)理論研究早期所做工作,絕非其貢獻(xiàn)的全部。但就本文內(nèi)容已經(jīng)可以看出,他的主要特點(diǎn)是理論思維方面的創(chuàng)新精神。雖然他畢生未做實(shí)驗(yàn)工作,但令人驚奇的是他對(duì)事物總保持高度敏感并且總能在數(shù)學(xué)上找到處理的方法。
-
諧波
+關(guān)注
關(guān)注
7文章
828瀏覽量
41825 -
電磁波
+關(guān)注
關(guān)注
21文章
1458瀏覽量
53872
原文標(biāo)題:S.A.謝昆諾夫?qū)Σ▽?dǎo)、天線理論的貢獻(xiàn)
文章出處:【微信號(hào):mwrfnet,微信公眾號(hào):微波射頻網(wǎng)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
相關(guān)推薦
基于Matlab的均勻平面電磁波的仿真
基于Matlab的平面電磁波的傳播、極化、反射和折射仿真設(shè)計(jì)
電磁波吸收體
電磁場(chǎng)的左性電磁波是怎么產(chǎn)生的?
電磁波引擎
電磁波簡(jiǎn)介
什么叫電磁波
電磁波正交極化,電磁波正交極化原理是什么?
電磁場(chǎng)與電磁波(第四版)課后答案__謝處方_共138頁(yè)
電磁波極化及其應(yīng)用
探索一下電磁波背后的故事
平面電磁波的三種極化
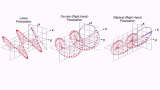




 一種科學(xué)思維上的敏感或直覺(jué),謝昆諾夫?qū)ζ矫骐姶挪ǖ男再|(zhì)深人的研究
一種科學(xué)思維上的敏感或直覺(jué),謝昆諾夫?qū)ζ矫骐姶挪ǖ男再|(zhì)深人的研究










評(píng)論