1985年，德國魯爾大學教授Depenbrock和日本學者Takahashi提出了直接轉矩控制理論，由于它直接控制定子磁鏈空間向量和電磁轉矩，使得控制系統得以簡化，并且提高了快速相應能力。直接轉矩控制不僅拓寬了向量控制理論，同時促進了電機現代控制技術的進一步發展。

SIMUUNK是MATLAB提供用來對動態系統進行建模、仿真、分析的軟件包。SIMULINK包含許多模塊庫，利用這些模塊庫可以很方便的進行復雜系統構建與仿真分析，為研究者提供了一個實用的仿真平臺。本文對基于MATLAB／SIMULINK異步電動機的直接轉矩控制離散系統仿真模型做出分析和介紹。

1 異步電機的數學模型

1．1 三相變兩相的物理意義

1．2 三相異步電機在α-β靜止坐標系下的電壓、磁鏈方程：

電機電壓方程為：

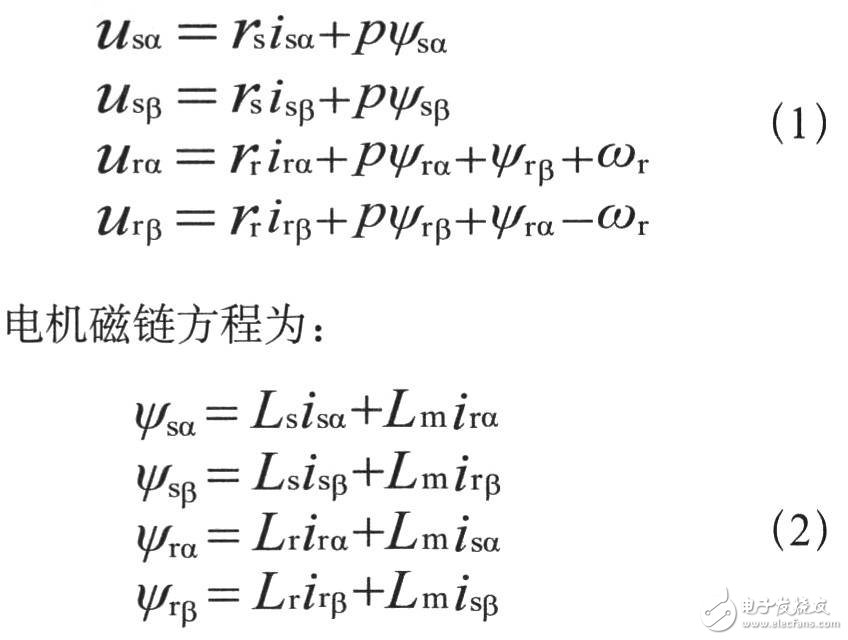
則電壓方程的矩陣形式為：

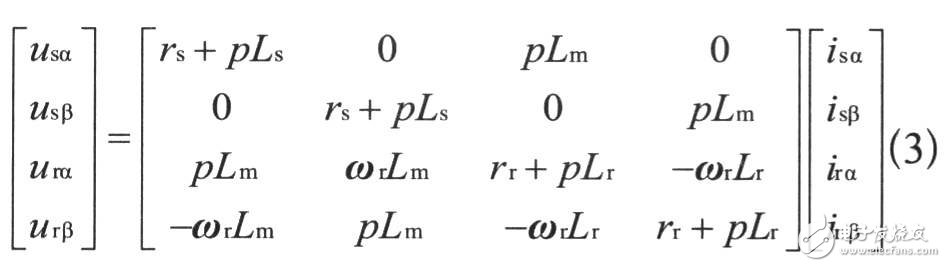
式中usα、usβ、isα、isβ分別是定子在α、β軸上電壓、電流分量；urα、urβ、irα、irβ分別是轉子在α、β軸上的電壓、電流分量；ψsα、ψsβ、ψrα、ψrβ分別是定子、轉子在α、β軸的磁鏈；Ls、Lr、Lm分別是定子繞組、轉子繞組及電機勵磁電感；P為微分算子；ωr是轉子的角速度。

1．3 電機的轉矩方程

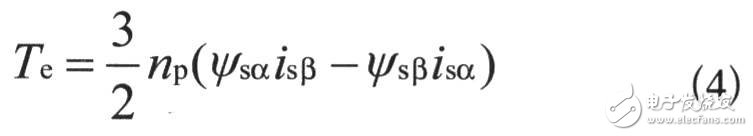
Te為電機的電磁轉矩；np為電機的極對數。

1．4 電機的運動方程

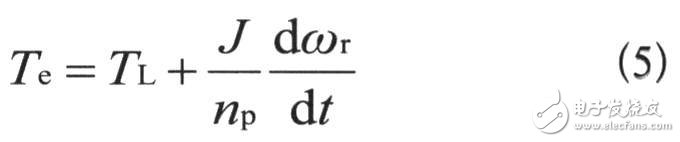
TL為負載轉矩；J為電機轉子和系統的轉動慣量。

根據異步電機的數學模型，利用SIMULINK的基本模塊及電機模塊搭建異步電機的仿真模型。

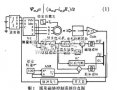
2 建立仿真模型

2．1 直接轉矩控制基本原理

定子、轉子磁鏈以及電磁轉矩可表示為：

在直接轉矩控制中，當定子磁鏈矢量ψs快速變化時，在很短暫時間內，可認為ψr不變，因此可以通過改變外加電壓矢量快速改變ψs，使定子磁鏈幅值|ψs|保持不變，同時控制定子磁鏈和轉子磁鏈的夾角θ，由式（6）可知，控制θ，實質上是控制電磁轉矩，即實現了轉矩的直接控制。

圖1所示為直接轉矩控制的系統框圖，包括異步電機模型、轉矩和磁鏈觀測器，滯環比較器，開關矢量選擇器和逆變器等部分。通過滯環比較得到調節信號，結合磁鏈位置信號SN和開關矢量選擇表，查表獲取此刻應作用于電機的電壓矢量，從而實現電機的直接轉矩控制。

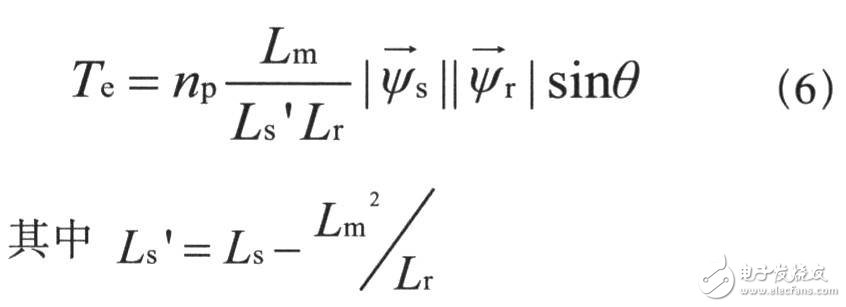
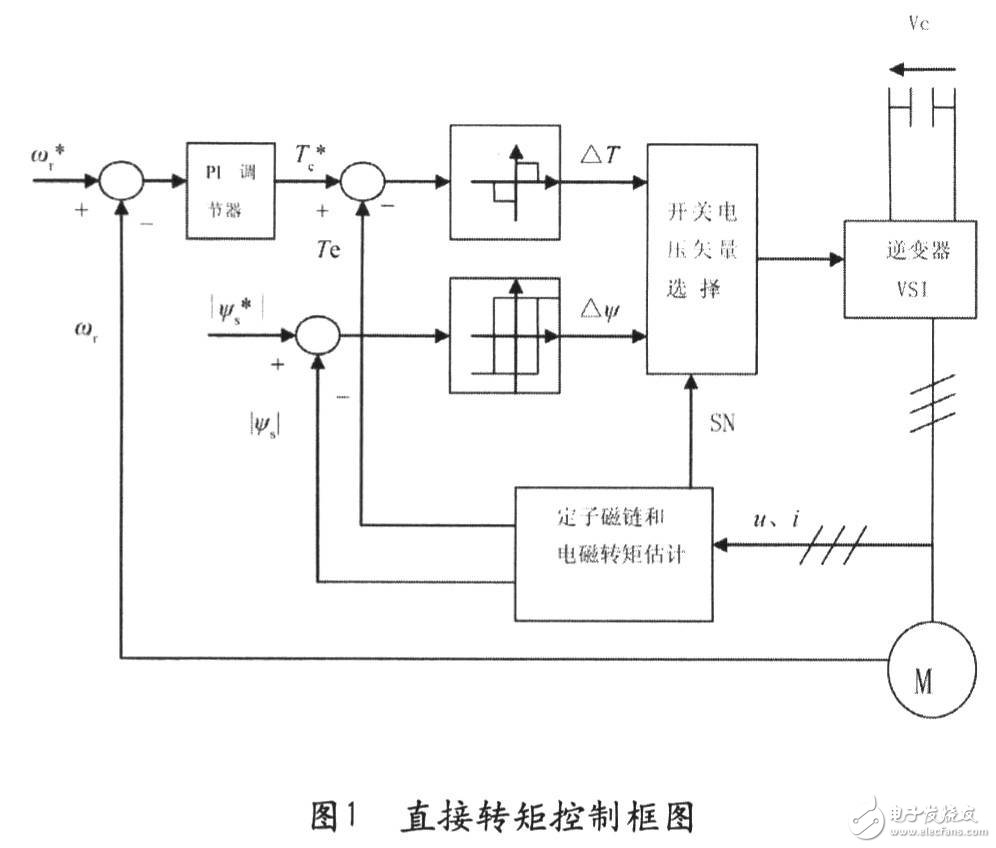
2．2 開關電壓矢量的合理選擇

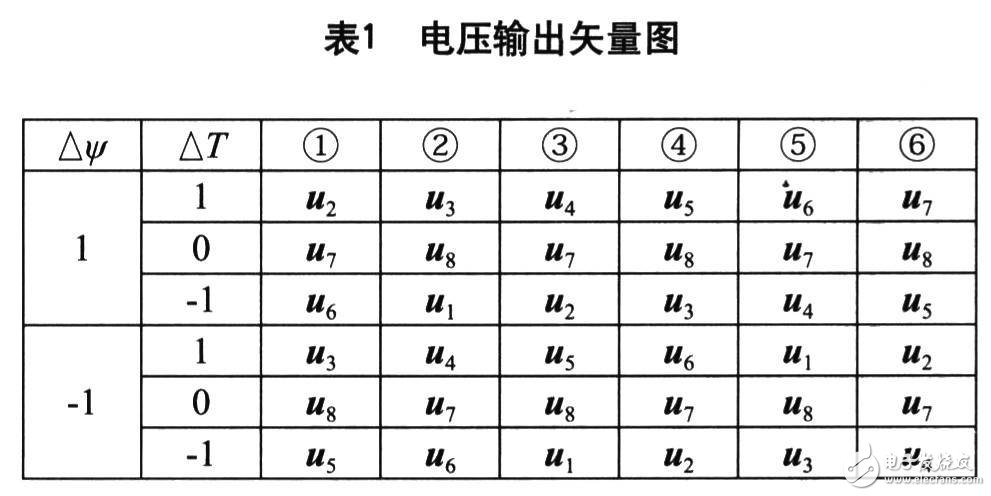
逆變器不同的開關狀態可產生如圖2中所示的u1～u6及u7，u8兩個零矢量。基于便于控制的考慮，把定子磁鏈所在空間位置劃分為①～⑥區間，總共六個扇區。

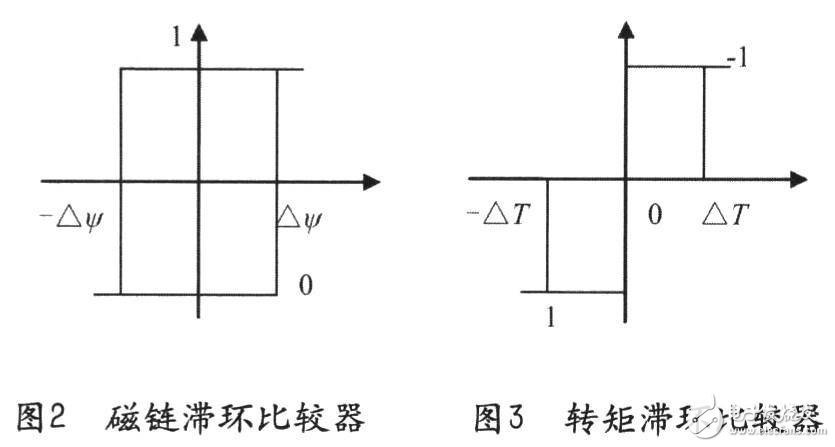
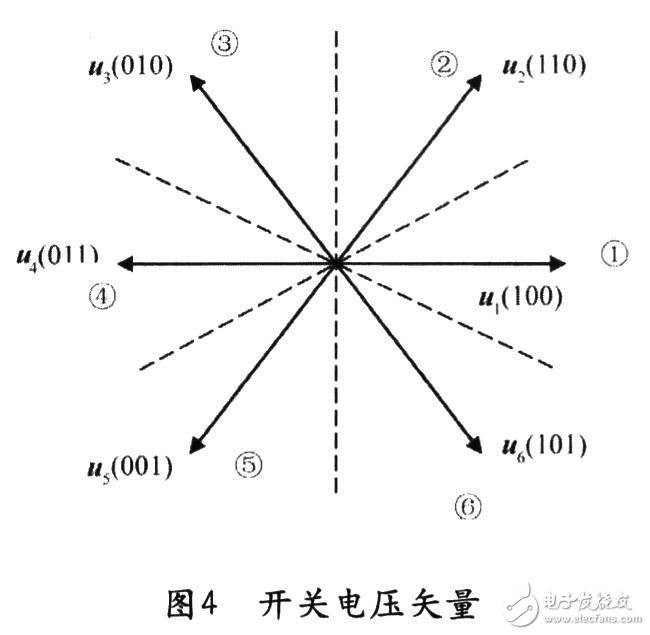
其中△ψ、△T的取值是根據滯環比較器的輸出來確定，即有：若|ψs|≤|ψsref|-|△ψs|，則△ψ=l；若|ψs|≥|ψsref|—|△ψs|，則△ψ=一1；若|Tc|≤|Tcref|—|△Te|，則△T=1；若|Tc|≥Tcref，則△T=0，若|Tc|≥|Tcref|-|△Tc|，則△T=一1；若|Tc|≤Tcref，則△T=0。依據圖4的磁鏈區間劃分、推理和控制經驗得到在磁鏈所在的區間的電壓輸出矢量表。

2．3 磁鏈觀測的離散仿真模型

磁鏈觀測采用定子磁鏈的u一i模型：

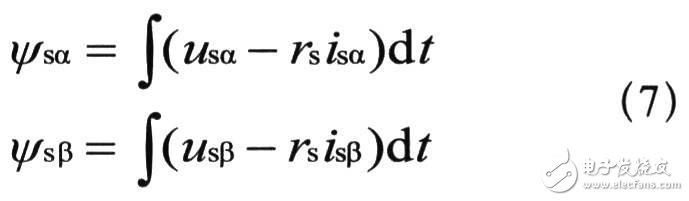
為了驗證離散直接轉矩控制的可行性，模型采用信號離散采樣的方式，將電壓、電流離散化，通過離散積分進行磁鏈觀測。

離散定子磁鏈觀測原理如下：

把定子電流、電壓和磁鏈離散化，式（7）可寫成下面的離散形式：

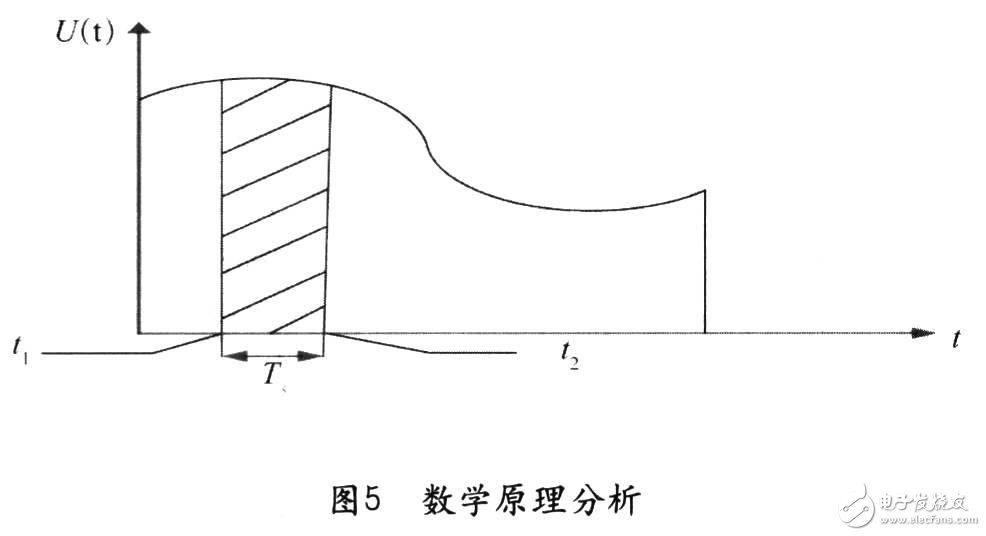
基于上面的推導就可以將通常的連續積分改為離散信號的積分，通過改變采樣時間Ts來對磁鏈和轉矩的估計精度進行調整。

3 仿真結果

設置電機的仿真參數，額定電壓380V，額定功率為2．5kW，極對數np=2，rs=0．435Ω，rr=0．816Ω，Ls=0．006H，Lm=0．08931H，Lr=0．006H，轉動慣量J=0．089kg．m2，轉矩滯環寬度為lN．m，磁鏈滯環寬度為0．02wb。

4 結論

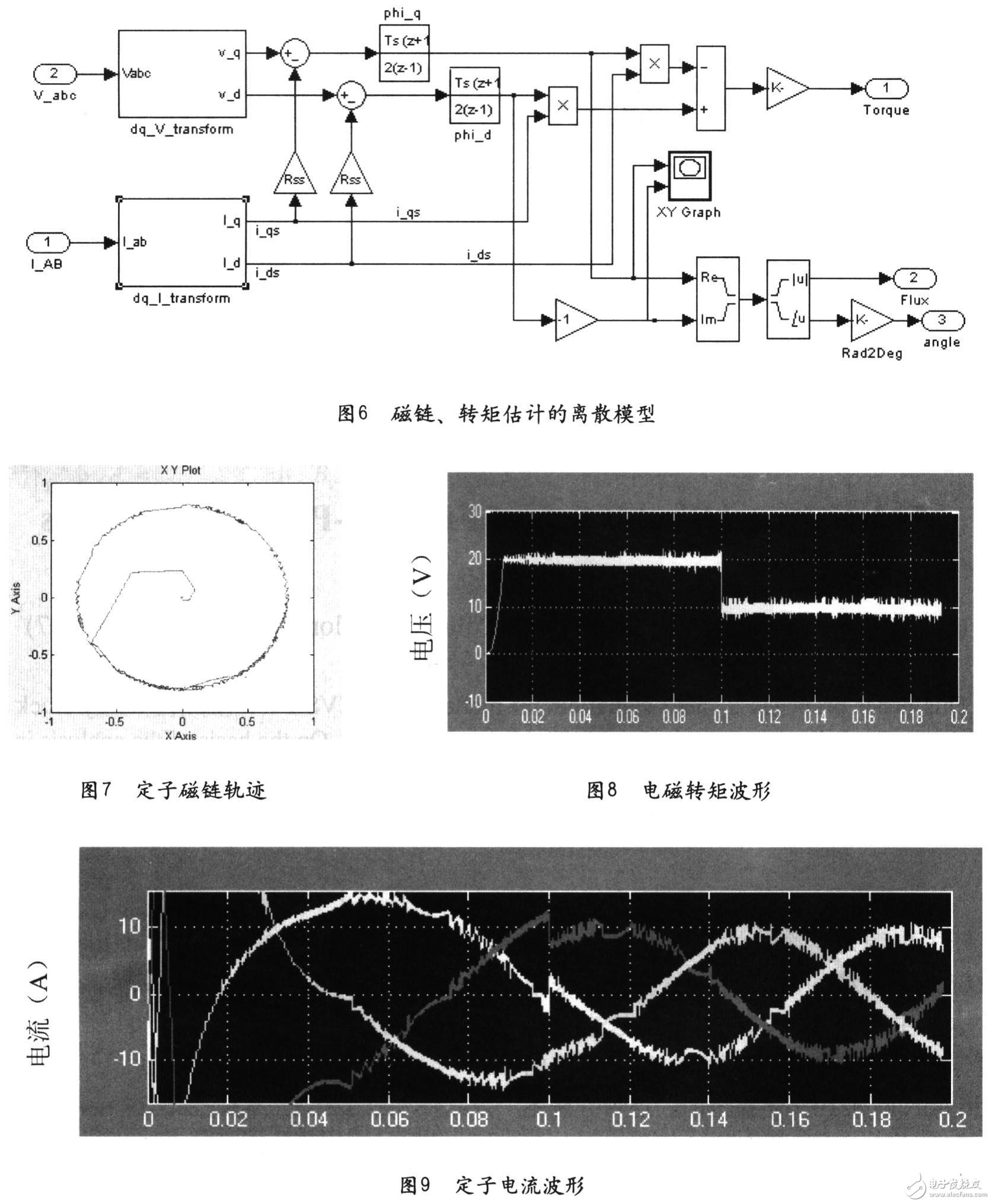
本文通過MaUab／simulink搭建出直接轉矩控制離散仿真系統，并進行仿真研究，得出定子磁鏈、轉矩、定子電流的波形（見圖7～圖9）。從仿真結果來看，圖7的定子磁鏈軌跡近似為圓形，圖9的定子電流近似為正弦波形，從而驗證了此離散模型的正確性。直接轉矩控制離散仿真系統為直接轉矩控制系統仿真提供了一種新思路，是一種有益的探索。