在學習數字信號處理時,很多種頻率很容易搞混淆,有模擬/數字/頻率/角頻率等等,也不是特別清楚不同頻率之間的關系,希望這篇文件可以為各種頻率來個了結.
4種頻率及其數量關系
實際物理頻率表示物理信號的真實頻率; fs為采樣頻率,表示ADC采集物理信號的頻率,由奈奎斯特采樣定理可以知道,fs必須≥信號最高頻率的2倍才不會發生信號混疊,因此fs能采樣到的信號最高頻率為fs/2。
角頻率Ω是物理頻率的2π倍, 這個也稱模擬頻率。
歸一化頻率是將物理頻率按fs歸一化之后的結果,最高的信號頻率為fs/2對應歸一化頻率0.5(ω=π),這也就是為什么在matlab的fdatool工具中歸一化頻率為什么最大只到0.5的原因。歸一化頻率中不含fs的信息.
圓周頻率是歸一化頻率的2*pi倍,這個也稱數字頻率ω。
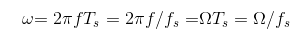
有關FFT頻率與實際物理頻率的分析
做n個點的FFT,表示在時域上對原來的信號取了n個點來做頻譜分析,n點FFT變換的結果仍為n個點。
換句話說,就是將2π數字頻率ω分成n份,而整個數字頻率ω的范圍覆蓋了從0-2π*fs的模擬頻率范圍。這里的fs是采樣頻率。而我們通常只關心0-π中的頻譜,因為根據奈科斯特定律,只有f=fs/2范圍內的信號才是被采樣到的有效信號。那么,在w的范圍內,得到的頻譜肯定是關于n/2對稱的。
舉例說,如果做了16個點的FFT分析,你原來的模擬信號的最高頻率f=32kHz,采樣頻率是64kHz,n的范圍是0,1,2...15。這時,64kHz的模擬頻率被分成了16分,每一份是4kHz,這個叫頻率分辨率。那么在橫坐標中,n=1時對應的f是4kHz, n=2對應的是8kHz, n=15時對應的是60kHz,你的頻譜是關于n=8對稱的。你只需要關心n=0到7以內的頻譜就足夠了,因為,原來信號的最高模擬頻率是32kHz。
這里可以有兩個結論:
必須知道原來信號的采樣頻率fs是多少,才可以知道每個n對應的實際頻率是多少,第k個點的實際頻率的計算為f(k)=k*(fs/n)
你64kHz做了16個點FFT之后,因為頻率分辨率是4kHz,如果原來的信號在5kHz或者63kHz有分量,你在頻譜上是看不見的,這就表示你越想頻譜畫得逼真,就必須取越多的點數來做FFT,n就越大,你在時域上就必須取更長的信號樣本來做分析。但是無論如何,由于離散采樣的原理,你不可能完全準確地畫出原來連續時間信號的真實頻譜,只能無限接近(就是n無限大的時候),這個就叫做頻率泄露。在采樣頻率fs不變得情況下,頻率泄漏可以通過取更多的點來改善,也可以通過做FFT前加窗來改善,這就是另外一個話題了。
為什么抽取/內插看起來對頻譜有影響?
在數字信號處理時,經常需要對數據進行抽取或者內插處理.抽取之后的頻率展寬了n倍,內插之后的頻率壓縮了n倍,從而需要在變采樣率之后添加抗混疊濾波器.但是實際上信號的頻率在抽取/內插的前后并沒有發生變化.這里的核心原因是:歸一化頻率失去了采樣率fs信息.
抽取和內插的實質是采樣率fs的變化
舉個例子:
我們設定fs=30.72MHz,使用3個cw信號的合成信號代表一個BW=8MHz的寬帶信號,使用實際頻率來表示信號,看到BW沒有變化,使用數字頻率w來表示信號,信號的BW似乎被壓縮了.
Q: 為什么要在歸一化頻率下來分析信號?
歸一化頻率
clear all;
close all;
fs = 30.72e6;
ts = 1/fs;
nFFT=4096;
%nFFT=32768;
t=0:ts:(nFFT-1)*ts;
d0=100*sin(2*pi*10e6*t);
d1=50*cos(2*pi*5e6*t);
d2=10*cos(2*pi*2e6*t);
dSum=d0+d1+d2;
dFFT = abs(fftshift(fft(dSum,nFFT)))/(nFFT/2);
%dFFT = abs(fft(dSum,nFFT))/(nFFT/2);
fAxis = (-1/2*nFFT:(1/2*nFFT-1))/nFFT*fs;
figure(1)
subplot(2,1,1)
plot(fAxis,dFFT)
subplot(2,1,2)
dSumI= zeros(1,2*nFFT);
for k =1:nFFT
dSumI(2*k) = dSum(k);
end
dFFTI = abs(fftshift(fft(dSumI,2*nFFT)))/(nFFT);
fAxisI = (-nFFT:(nFFT-1))/(2*nFFT)*fs*2; %fs double
plot(fAxisI,dFFTI)
title(‘interpolated signal’)
figure(2)
subplot(2,1,1)
wAxis = 2*pi*(-1/2*nFFT:(1/2*nFFT-1))/(nFFT);
plot(wAxis,dFFT)
set(gca,‘XTick’,-2*pi:pi/2:2*pi)
title(‘original signal normalize’)
subplot(2,1,2)
wAxisI = 2*pi*(-nFFT:(nFFT-1))/(2*nFFT);
plot(wAxisI,dFFTI)
set(gca,‘XTick’,-2*pi:pi/2:2*pi)
title(‘interpolated signal normalize’)
-
數字信號處理
+關注
關注
15文章
563瀏覽量
45952 -
頻率
+關注
關注
4文章
1534瀏覽量
59327
發布評論請先 登錄
相關推薦




 數字信號處理技術中不同頻率之間的關系
數字信號處理技術中不同頻率之間的關系











評論