一頁PPT證明黎曼猜想
據(jù)中國之聲《新聞縱橫》報道,159年前,德國數(shù)學(xué)家黎曼在題為《論小于給定數(shù)值的素數(shù)個數(shù)》的論文中提出的“黎曼猜想”,一直以來被視作“純數(shù)學(xué)領(lǐng)域最重要的問題之一”。盡管無數(shù)一流數(shù)學(xué)家向證明黎曼猜想發(fā)起沖擊,卻無一人能成功——不過就在昨天(9月24號),著名數(shù)學(xué)家、菲爾茲獎和阿貝爾獎雙料得主阿蒂亞爵士或?qū)⒊蔀檫@樣一個劃時代的人物。
德國海德堡當(dāng)?shù)貢r間9月24號上午,阿蒂亞爵士作為海德堡論壇第二位宣講嘉賓,公布了他對黎曼猜想的證明。他表示,自己基于馮·諾依曼、希策布魯赫和狄拉克等人的成果,使用一種“簡單而全新”的方法證明了黎曼猜想,引發(fā)了全世界數(shù)學(xué)家們的關(guān)注。
Michael Atiyah 介紹了素數(shù)研究的歷史以及素數(shù)與黎曼猜想的關(guān)系
45分鐘證明演講中,有30分鐘介紹歷史
長期關(guān)注人工智能、機器學(xué)習(xí)領(lǐng)域的垂直媒體“機器之心”昨天全程記錄了阿蒂亞爵士在論壇上有關(guān)黎曼猜想的宣講直播。機器之心聯(lián)合創(chuàng)始人、副主編李亞洲向中國之聲介紹說,在9月24號的海德堡獲獎?wù)哒搲希钍荜P(guān)注的可能就是阿蒂亞爵士黎曼證明的宣講了,也因為看直播的人數(shù)太多,導(dǎo)致官方直播流崩潰,組織方不得不改用手機直播。其實整個45分鐘演講中,阿蒂亞花了近30分鐘的時間介紹歷史:素數(shù)、黎曼猜想的歷史。中間他也開玩笑說,如果你解決了黎曼猜想,你會出名,但如果你已經(jīng)是個名人,(解黎曼猜想)那就會有聲名狼藉的風(fēng)險”。
因此,可以看出,雖然已經(jīng)89歲高齡,但阿蒂亞爵士一直在自己的領(lǐng)域努力著。也許,這其實也是阿蒂亞爵士今天想傳達(dá)的精神。
“這個證明的對與錯現(xiàn)在還不明確”
在介紹完歷史之后,他就開始介紹Todd函數(shù)以及最核心的一頁PPT(也就是Todd函數(shù)如何幫助證明黎曼猜想的PPT)。阿蒂亞爵士對證明思路的介紹并沒有多少,以至于直播間有人調(diào)侃30分鐘歷史介紹,一頁PPT證明。最后,阿蒂亞爵士給后輩們提供了建議:就是最后一張PPT提到的四個建議,包括運用如今最強大的工具;驗證所有著名的猜想(無論是證明過的還是未證明的);判斷出哪些難題可高效計算出;以及決定哪些難題是有時間做的。
整個直播過程中,Twitter上、直播間中的實時討論與評價,這個證明的對與錯現(xiàn)在還不明確,可能經(jīng)過一段時間的發(fā)酵能看的更清楚。
黎曼ζ 函數(shù)
黎曼猜想到底是啥
黎曼猜想是關(guān)于素數(shù),又叫質(zhì)數(shù)的問題,是為了研究素數(shù)分布規(guī)律。“一個大于1的自然數(shù),除了1和它自身外,不能整除其他自然數(shù)的數(shù)叫做素數(shù)”——這個概念相信很多人第一次接觸是在上小學(xué)的時候。雖然定義簡單且容易理解,但是數(shù)學(xué)家們卻為尋找一個更為精確地表達(dá)公式而不斷努力。
德國數(shù)學(xué)家黎曼在《論不超過一個給定值的素數(shù)的個數(shù)》中提出:素數(shù)的分布奧秘與一個復(fù)雜的函數(shù)密切相關(guān),他在文中定義了一個被后世成為“Zeta”的無窮極函數(shù)。黎曼猜測,可能所有非平凡零點都全部位于實部等于1/2的直線上,這條線被稱為臨界線。這就是令后世數(shù)學(xué)家魂牽夢繞卻輾轉(zhuǎn)反側(cè)的“黎曼猜想”。
物理學(xué)博士、科普作家盧昌海這樣解釋:“黎曼當(dāng)年提出一個猜想,就是黎曼Zeta函數(shù)的所有的非平凡零點都正好排在復(fù)平面上的一條直線上,那么這條直線被稱為臨界線。雖然表面上看只是關(guān)于一個復(fù)平面函數(shù)的猜想,實際上它是跟素數(shù)分布有非常密切的關(guān)系。”
黎曼猜想若被證明將增加一千多條數(shù)學(xué)定理
數(shù)學(xué)界的知名難題——黎曼猜想到底有多重要?盧昌海告訴中國之聲記者:“現(xiàn)在數(shù)學(xué)界有超過一千條數(shù)學(xué)命題,它是以黎曼猜想的成立為前提的,也就是說它的表述都是‘假如一旦猜想或者他的某種廣義形式成立,那么我們可以有這樣一個結(jié)果’。黎曼猜想如果被證明,那么數(shù)學(xué)上幾乎一夜之間就可以增添一千多條定理——因為那些原來是有條件成立的命題,就全都變成定理了。如果黎曼猜想被證偽的話,那么估計就是一千多條(定理)里面,其中有一些也就不會成立了。所以反方面的影響也是比較大的。那么對現(xiàn)實應(yīng)用來說,目前據(jù)我所知并沒有什么特別的影響,主要是對純數(shù)學(xué)。”
“世紀(jì)之謎”黎曼猜想如何證明?核心論點是什么?在宣講現(xiàn)場,阿蒂亞爵士僅僅寥寥數(shù)頁PPT進(jìn)行了闡釋。此前有很多人猜測,阿蒂亞爵士會使用量子力學(xué)來證明黎曼猜想,但在演講中他表示證明黎曼猜想的是一個名為Todd的函數(shù)。那么黎曼猜想被證明后,有何用處?阿蒂亞爵士的回答是,黎曼猜想能推廣到多種情況,并且一步步得到證明,它的證明對年輕的數(shù)學(xué)、計算機科學(xué)、邏輯學(xué)和物理學(xué)研究者非常重要。
物理學(xué)博士:尚未看到有分量的專家評價
根據(jù)深科技的報道,阿蒂亞爵士稱,他關(guān)于精細(xì)結(jié)構(gòu)常數(shù)α(念阿爾法)的相關(guān)論文已投稿至英國皇家學(xué)會。介于這篇文章目前還未經(jīng)過同行審議,一些學(xué)者對他的推演過程存疑。同樣,也有學(xué)者對此次黎曼猜想的證明過程質(zhì)疑。當(dāng)然,還一些學(xué)者認(rèn)為,阿蒂亞爵士的思路或為后續(xù)黎曼猜想證明提供了一種新思路。
雖然歷史上也有人曾宣稱自己“證明了黎曼猜想”,但是最終都被發(fā)現(xiàn)存在嚴(yán)重的漏洞。如何才能真正證明黎曼猜想?盧昌海昨晚文字回復(fù)中國之聲記者稱,雖然具體方法可以千變?nèi)f化。如果是證明黎曼猜想不成立,則相對“簡單”些,舉出一個反例亦可達(dá)到目的。
阿蒂亞結(jié)束演講后,現(xiàn)場響起了熱烈掌聲,然而論證本身最終能否經(jīng)得起考驗,還得通過專家們的苛刻審核。物理學(xué)博士、科普作家盧昌海表示,目前尚未看到有分量的專家評價——但考慮到阿蒂亞爵士的身份,如果專家認(rèn)為這一報告完全不構(gòu)成證明,出于對爵士的敬重他們或許會保持緘默。
-
人工智能
+關(guān)注
關(guān)注
1793文章
47539瀏覽量
239394 -
機器學(xué)習(xí)
+關(guān)注
關(guān)注
66文章
8434瀏覽量
132868
原文標(biāo)題:“黎曼猜想”被證明? 這個證明的對與錯現(xiàn)在還不明確,學(xué)者:未看到有分量專家評價
文章出處:【微信號:eetop-1,微信公眾號:EETOP】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
BitEnergy AI公司開發(fā)出一種新AI處理方法
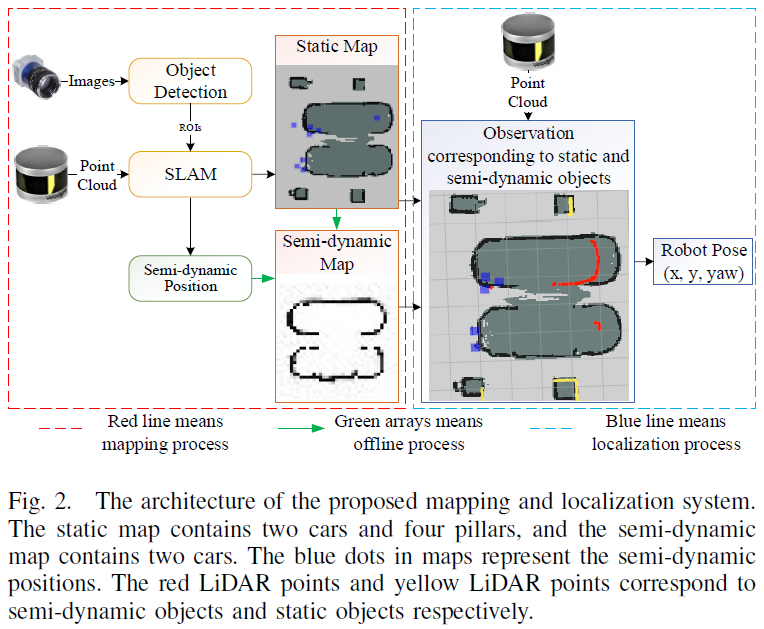
一種半動態(tài)環(huán)境中的定位方法
圖靈測試的內(nèi)容是什么_圖靈測試的作用
rup是一種什么模型
神經(jīng)網(wǎng)絡(luò)在數(shù)學(xué)建模中的應(yīng)用
有動靜!先楫出了顆適用機器人的MCU!

【《計算》閱讀體驗】開卷有益,全書與導(dǎo)論
基于助聽器開發(fā)的一種高效的語音增強神經(jīng)網(wǎng)絡(luò)
一種利用光電容積描記(PPG)信號和深度學(xué)習(xí)模型對高血壓分類的新方法
江西薩瑞微獨家研發(fā)【一種LDMOS場效應(yīng)管及其制備方法】

基于DE1-SOC的String Art實現(xiàn)





 一種“簡單而全新”的方法證明了黎曼猜想,引發(fā)了全世界數(shù)學(xué)家們的關(guān)注
一種“簡單而全新”的方法證明了黎曼猜想,引發(fā)了全世界數(shù)學(xué)家們的關(guān)注










評論