近年來,深度學(xué)習(xí)受到全球關(guān)注。成就最為突出的便是深度強(qiáng)化學(xué)習(xí),例如Alpha Go等。本文作者Artem Oppermann基于此,對深度強(qiáng)化學(xué)習(xí)訓(xùn)練AI智能體所需要的數(shù)學(xué)背景知識——馬爾科夫鏈做了深入淺出的介紹。
近年來,世界各地的研究員和媒體對深度學(xué)習(xí)極其關(guān)注。而深度學(xué)習(xí)方面成就最為突出的就是深度強(qiáng)化學(xué)習(xí)——從谷歌Alpha Go擊敗世界頂級棋手,到DeepMind的AI智能體自學(xué)走路、跑步以及躲避障礙物,如下圖所示:
圖2:AI智能體學(xué)習(xí)如何跑步、躲避跨越障礙物
圖3:AI智能體學(xué)習(xí)如何跑步、躲避跨越障礙物
還有一些AI智能體打破了自2014年以來人類玩家在雅達(dá)利游戲中的最高紀(jì)錄。
圖4:AI智能體學(xué)習(xí)如何玩兒雅達(dá)利游戲
而這一切最令人驚奇的是這些AI智能體中,沒有一個(gè)是由人類明確編程或者指導(dǎo)他們?nèi)绾瓮瓿蛇@些任務(wù)的。他們僅僅是通過深度學(xué)習(xí)和強(qiáng)化學(xué)習(xí)的力量在自學(xué)!
本文作者Artem Oppermann在Medium中開設(shè)了《自學(xué)AI智能體》的“連載”課程,本文是其第一篇文章,詳細(xì)介紹了AI智能體自學(xué)完成任務(wù)這一過程背后需要了解的數(shù)學(xué)知識——馬爾可夫鏈。
Nutshell中的深度強(qiáng)化學(xué)習(xí)
深度強(qiáng)化學(xué)習(xí)可以概括為構(gòu)建一種算法(或AI智能體),直接從與環(huán)境的交互中學(xué)習(xí)。
圖5:深度強(qiáng)化學(xué)習(xí)示意圖
環(huán)境可以是真實(shí)世界,電腦游戲,模擬,甚至棋盤游戲,比如圍棋或象棋。就像人類一樣,人工智能代理人從其行為的結(jié)果中學(xué)習(xí),而不是從明確的教導(dǎo)中學(xué)習(xí)。
在深度強(qiáng)化學(xué)習(xí)中,智能體是由神經(jīng)網(wǎng)絡(luò)表示的。神經(jīng)網(wǎng)絡(luò)直接與環(huán)境相互作用。它觀察環(huán)境的當(dāng)前狀態(tài),并根據(jù)當(dāng)前狀態(tài)和過去的經(jīng)驗(yàn)決定采取何種行動(dòng)(例如向左、向右移動(dòng)等)。根據(jù)采取的行動(dòng),AI智能體收到一個(gè)獎(jiǎng)勵(lì)(Reward)。獎(jiǎng)勵(lì)的數(shù)量決定了在解決給定問題時(shí)采取的行動(dòng)的質(zhì)量(例如學(xué)習(xí)如何走路)。智能體的目標(biāo)是學(xué)習(xí)在任何特定的情況下采取行動(dòng),使累積的獎(jiǎng)勵(lì)隨時(shí)間最大化。
馬爾可夫決策過程
馬爾可夫決策過程(MDP)是一個(gè)離散時(shí)間隨機(jī)控制過程。
MDP是迄今為止我們對AI智能體的復(fù)雜環(huán)境建模的最佳方法。智能體要解決的每個(gè)問題都可以看作是S1、S2、S3、……Sn(狀態(tài)可以是圍棋/象棋的棋局配置)的序列。智能體采取行動(dòng)并從一個(gè)狀態(tài)移動(dòng)到另一個(gè)狀態(tài)。
馬爾可夫過程
馬爾可夫過程是一個(gè)描述可能狀態(tài)序列的隨機(jī)模型,其中當(dāng)前狀態(tài)僅依賴于以前的狀態(tài)。這也被稱為馬爾科夫性質(zhì)(公式1)。對于強(qiáng)化學(xué)習(xí),這意味著AI智能體的下一個(gè)狀態(tài)只依賴于最后一個(gè)狀態(tài),而不是之前的所有狀態(tài)。

公式1:馬爾可夫性質(zhì)
馬爾可夫過程是一個(gè)隨機(jī)過程。這意味著從當(dāng)前狀態(tài)s到下一個(gè)狀態(tài)s'的轉(zhuǎn)變“只能在一定概率下發(fā)生”(公式2)。在馬爾科夫過程中,一個(gè)被告知向左移動(dòng)的智能體只會在一定概率下向左移動(dòng),例如0.998。在概率很小的情況下,由環(huán)境決定智能體的最終位置。

公式2:從狀態(tài)s到狀態(tài)s'的轉(zhuǎn)變概率
Pss '可以看作是狀態(tài)轉(zhuǎn)移矩陣P中的一個(gè)條目,它定義了從所有狀態(tài)s到所有后續(xù)狀態(tài)s'的轉(zhuǎn)移概率(公式3)。

公式3:轉(zhuǎn)移概率矩陣
馬爾可夫獎(jiǎng)勵(lì)(Reward)過程
馬爾可夫獎(jiǎng)勵(lì)過程是一個(gè)元組

公式4:在狀態(tài)s中期望獲得獎(jiǎng)勵(lì)
總獎(jiǎng)勵(lì)Gt(公式5),它是智能體在所有狀態(tài)序列中所獲得的預(yù)期累積獎(jiǎng)勵(lì)。每個(gè)獎(jiǎng)勵(lì)都由所謂的折扣因子γ∈[0,1]加權(quán)。

公式5:所有狀態(tài)的獎(jiǎng)勵(lì)總額
價(jià)值函數(shù)(Value Function)
另一個(gè)重要的概念是價(jià)值函數(shù)v(s)中的一個(gè)。價(jià)值函數(shù)將一個(gè)值映射到每個(gè)狀態(tài)s。狀態(tài)s的值被定義為AI智能體在狀態(tài)s中開始其進(jìn)程時(shí)將得到的預(yù)期總獎(jiǎng)勵(lì)(公式6)。

公式6:價(jià)值函數(shù),從狀態(tài)s開始的期望返回值
價(jià)值函數(shù)可以分解為兩個(gè)部分:
處于狀態(tài)s時(shí),智能體收到的即使獎(jiǎng)勵(lì)(immediate reward)R(t+1);
在狀態(tài)s之后的下一個(gè)狀態(tài)的折現(xiàn)值(discounted value)v(s(t+1));

公式7:價(jià)值函數(shù)的分解
貝爾曼方程
馬爾可夫獎(jiǎng)勵(lì)過程的貝爾曼方程
分解后的值函數(shù)(公式8)也稱為馬爾可夫獎(jiǎng)勵(lì)過程的貝爾曼方程。
該函數(shù)可以在節(jié)點(diǎn)圖中可視化(圖6),從狀態(tài)s開始,得到值v(s)。在狀態(tài)s中,我們有特定的概率Pss '到下一個(gè)狀態(tài)s'中結(jié)束。在這種特殊情況下,我們有兩個(gè)可能的下一個(gè)狀態(tài)為了獲得值v(s),我們必須總結(jié)由概率Pss'加權(quán)的可能的下一個(gè)狀態(tài)的值v(s'),并從狀態(tài)s中添加直接獎(jiǎng)勵(lì)。 這就產(chǎn)生了公式9,如果我們在等式中執(zhí)行期望算子E,那么這只不是公式8。

公式8:價(jià)值函數(shù)分解

圖6:從s到s'的隨機(jī)轉(zhuǎn)變

公式9:執(zhí)行期望算子E后的貝爾曼方程
馬爾可夫決策過程——定義
馬爾可夫決策過程是一個(gè)有決策的馬爾可夫獎(jiǎng)勵(lì)過程。
馬爾可夫決策過程是馬爾可夫獎(jiǎng)勵(lì)過程的決策。 馬爾可夫決策過程由一組元組

公式10:期望獎(jiǎng)勵(lì)取決于狀態(tài)s中的行為
策略
在這一點(diǎn)上,我們將討論智能體如何決定在特定狀態(tài)下必須采取哪些行動(dòng)。 這由所謂的策略π(公式11)決定。 從數(shù)學(xué)角度講,策略是對給定狀態(tài)的所有行動(dòng)的分配。 策略確定從狀態(tài)s到智能體必須采取的操作a的映射。

公式11:策略作為從s到a的一個(gè)映射
該策略導(dǎo)致狀態(tài)價(jià)值函數(shù)v(s)的新定義(公式12),我們現(xiàn)在將其定義為從狀態(tài)s開始的預(yù)期返回,然后遵循策略π。

公式12:狀態(tài)值函數(shù)
動(dòng)作價(jià)值函數(shù)
除狀態(tài)值函數(shù)之外的另一個(gè)重要功能是所謂的動(dòng)作值函數(shù)q(s,a)(公式13)。 動(dòng)作值函數(shù)是我們通過從狀態(tài)s開始,采取行動(dòng)a然后遵循策略π獲得的預(yù)期回報(bào)。 請注意,對于狀態(tài)s,q(s,a)可以采用多個(gè)值,因?yàn)橹悄荏w可以在狀態(tài)s中執(zhí)行多個(gè)操作。 Q(s,a)的計(jì)算是通過神經(jīng)網(wǎng)絡(luò)實(shí)現(xiàn)的。 給定狀態(tài)作為輸入,網(wǎng)絡(luò)計(jì)算該狀態(tài)下每個(gè)可能動(dòng)作的質(zhì)量作為標(biāo)量(圖7)。 更高的質(zhì)量意味著在給定目標(biāo)方面采取更好的行動(dòng)。

圖7:動(dòng)作價(jià)值函數(shù)說明
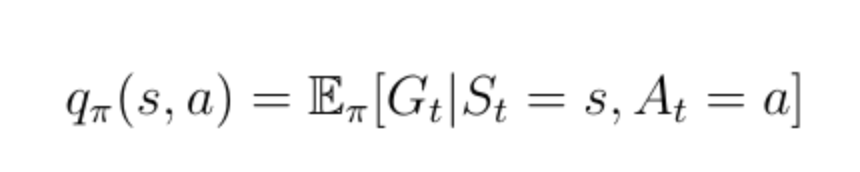
公式13:動(dòng)作價(jià)值函數(shù)
狀態(tài)值函數(shù)v(s)可以分解為以下形式:

公式14:狀態(tài)價(jià)值函數(shù)分解
同樣的分解也適用于動(dòng)作價(jià)值函數(shù):

公式15:動(dòng)作價(jià)值函數(shù)分解
在這一點(diǎn)上,我們討論v(s)和q(s,a)如何相互關(guān)聯(lián)。 這些函數(shù)之間的關(guān)系可以在圖中再次可視化:

圖8:v(s)和q(s,a)之間關(guān)系的可視化
在這個(gè)例子中,處于狀態(tài)s允許我們采取兩種可能的行動(dòng)a,根據(jù)定義,在特定狀態(tài)下采取特定的行動(dòng)給了我們動(dòng)作值q(s,a)。價(jià)值函數(shù)v(s)是概率q(s,a)的和,由在狀態(tài)s中采取行動(dòng)a的概率來賦予權(quán)重。

公式16:狀態(tài)值函數(shù)是動(dòng)作值的加權(quán)和
現(xiàn)在讓我們考慮圖9中的相反情況。二叉樹的根現(xiàn)在是一個(gè)我們選擇采取特定動(dòng)作的狀態(tài)。 請記住,馬爾可夫過程是隨機(jī)的。 采取行動(dòng)并不意味著你將以100%的確定性結(jié)束你想要的目標(biāo)。 嚴(yán)格地說,你必須考慮在采取行動(dòng)后最終進(jìn)入其他狀態(tài)的概率。 在采取行動(dòng)后的這種特殊情況下,你可以最終處于兩個(gè)不同的下一個(gè)狀態(tài)s':

圖9:v(s)與q(s,a)關(guān)系的可視化
為了獲得動(dòng)作值,你必須用概率加權(quán)的折現(xiàn)狀態(tài)值來最終得到所有可能的狀態(tài)(在本例中僅為2),并加上即時(shí)獎(jiǎng)勵(lì):
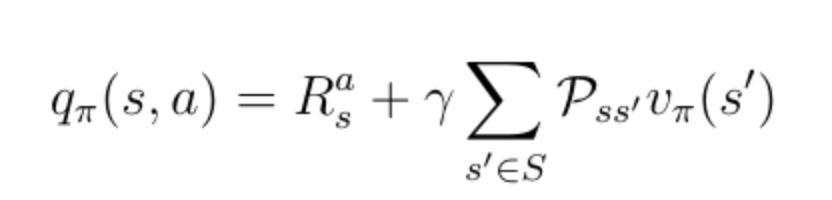
公式17:q(s,a)和v(s)之間的關(guān)系
既然我們知道了這些函數(shù)之間的關(guān)系,我們就可以將公式16中的v(s)插入公式17中的q(s,a)中。我們得到公式18,可以看出當(dāng)前的q(s,a)和下一個(gè)動(dòng)作值q(s,a)之間存在遞歸關(guān)系。

公式18:動(dòng)作值函數(shù)的遞歸性質(zhì)
這種遞歸關(guān)系可以再次在二叉樹中可視化(圖10)。
圖10:q(s,a)遞歸行為的可視化
-
智能體
+關(guān)注
關(guān)注
1文章
162瀏覽量
10599 -
強(qiáng)化學(xué)習(xí)
+關(guān)注
關(guān)注
4文章
268瀏覽量
11274
原文標(biāo)題:AlphaGo等智能體是如何煉成的?你需要懂得馬爾科夫鏈
文章出處:【微信號:AI_era,微信公眾號:新智元】歡迎添加關(guān)注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關(guān)推薦
強(qiáng)悍版智能小車
設(shè)計(jì)完P(guān)CB后走線不能躲避障礙物時(shí)什么情況
求教 障礙物感應(yīng)類開關(guān)
越障小車電機(jī)、輪胎選擇
智能壁障車
基于AT89S52芯片的簡易智能小車的設(shè)計(jì)
遇障礙物時(shí) 語音提示 前方危險(xiǎn),請注意。
基于labview機(jī)器視覺的障礙物時(shí)別
新人求教AD中Pullback(障礙物)到底是一個(gè)什么概念或作用?
ANYmal機(jī)器人具有腿和腳,可跨越障礙物
障礙物檢測實(shí)驗(yàn)
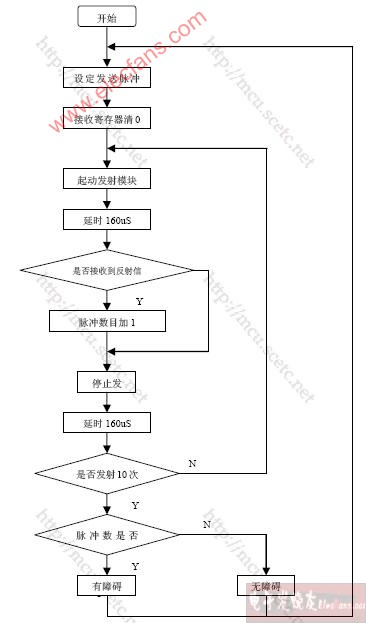
障礙物方位檢測實(shí)驗(yàn)




 AI智能體學(xué)習(xí)如何跑步、躲避跨越障礙物
AI智能體學(xué)習(xí)如何跑步、躲避跨越障礙物










評論