在經典力學中，當粒子攜帶的能量不足以克服勢壘時，粒子是無法穿過勢壘的。但是在量子力學中，電荷等微觀粒子卻能夠穿越大于其自身攜帶總能量的勢壘層，這就是量子隧穿效應。我們可以使用 COMSOL? 軟件的“半導體模塊”中提供的 WKB 隧穿模型來以及異質結和肖特基等邊界條件，描述量子隧穿的相關現象。在下文中，我們將通過基準模型演示其用法。

Wentzel-Kramers-Brillouin 近似

根據 K.Yang、J.R.East 和 G.I. Haddad 的參考文獻（Ref. 1），若采用 Wentzel-Kramers-Brillouin（WKB）近似假設，隧穿電流會向熱離子電流增加一個分數因子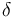

(1)

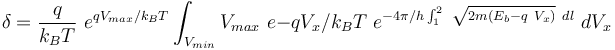
其中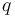

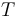
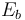
內積分

WKB 隧穿模型

為了使用 WKB 近似模擬隧穿效應，首先需要設置邊界條件，此步驟涉及添加隧穿產生的額外電流密度。針對異質結，選擇熱電子發射；針對金屬接觸，選擇理想肖特基。選定上述（非默認）選項之后，新建的額外電流貢獻 欄將立即顯示在界面中，我們即可為電子和空穴分別指定額外電流貢獻。默認情況下，不需要添加額外電流。我們還可以在內置的 WKB 隧穿模型和用戶定義選項間進行選擇。請參考下方示例截圖。

選擇熱電子發射以添加額外電流貢獻。

如上文所述，對于與勢壘相關的變量，電子和空穴的計算方式不同，所以我們為每種類型的載流子引入了不同的特征，它們在“模型開發器”中被添加到異質結或肖特基接觸邊界條件的子節點。請參考下方示例截圖。

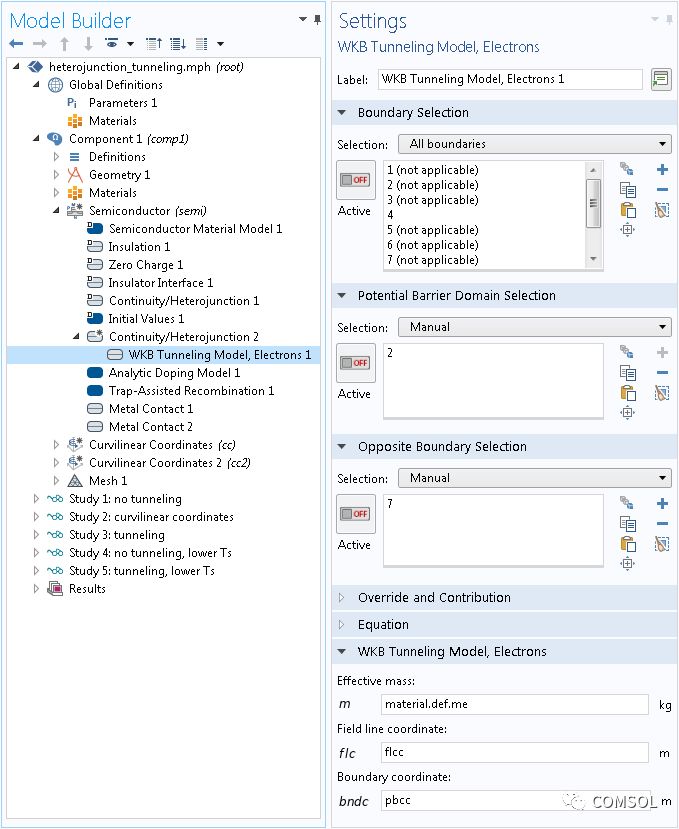
“模型開發器”的樹結構和 WKB 隧穿模型，電子 特征的設置窗口。

在上圖的設置 窗口中，邊界選擇 通常指定添加了額外電流密度的邊界。域選擇則指定勢壘所在的相鄰域。第二個邊界選擇指定了與第一個邊界選擇相對的域的邊界。隧穿基本發生在選定域內，即第一個和第二個邊界選擇之間。

在二維和三維模型中，除了有效質量之外，我們還需要輸入一個描述電場線方向的坐標變量，并輸入一個（二維）或兩個（三維）跨過隧穿邊界的坐標變量。在簡單的矩形幾何中，內置空間變量x，y和z（或基于它們的表達式）可用于定義坐標變量。在更通用的幾何中，則可以使用曲線坐標 數學接口。“案例下載”中的“異質結隧穿”教學模型演示了后一種方法。

漸變異質結模型

異質結隧穿模型比較了在不同溫度下，發生與不發生隧穿效應的漸變異質結的電流密度模擬值。為了便于比較仿真結果，設備構型和所有材料屬性均來源于參考文獻（特別是 3.3 節）。

這是一個分子束外延生長的 AlxGa1-xAs 漸變異質結，它形成了可阻擋電子的三角形勢壘。為了獲得與實驗數據的最佳擬合，文獻作者在運行每個仿真時使用了一組未必與實驗標稱值相同的材料及設備參數。為了方便比較仿真結果，我們采用了作者選定的一組模擬參數，理由與文獻提出的論點一致。

我們通過在空間上改變 AlxGa1-xAs 層中鋁的摩爾分數來形成三角形勢壘層。在 COMSOL Multiphysics? 軟件中，我們能夠基于摩爾分數等局部變量，以及參考溫度、晶格溫度和摻雜濃度等參數和變量，直接創建材料并定義材料屬性。摩爾分數則通過空間變化變量來定義。使變量在空間中變化有兩種方法：使用顯式表達式，或者在不同域內使用不同定義。我們在模型中利用了這兩種方法。如下方截圖所示，我們在定義下創建了多個變量節點，在不同域內應用不同的摻雜變量和摩爾分數。此外，我們利用內置的空間坐標變量 x 使摩爾分數在“域 2”內具有空間依賴性。

通過在 定義下添加多個節點（每個域對應一個節點），對不同的域應用不同的摻雜與摩爾分數變量。內置變量 x 使變量Al_frac具有空間依賴性。

上文所定義的空間依賴性變量可以用在材料與物理場的定義中，如下圖所示。

我們將摻雜變量N_D直接輸入到摻雜特征中，如下方截圖所示。

在摻雜濃度的定義中使用空間因變量N_D。

我們利用摩爾分數變量Al_frac在材料定義中定義了一個便捷符號 x，此符號位于基本子節點的設置窗口的局部屬性欄中，并被用于定義態密度（DOS）有效質量、相對介電常數、帶隙、電子親和性和遷移率。請注意，利用前綴 def，我們可以訪問定義在基本 子節點中、帶def標簽的符號。例如，在下方截圖中，輸入框中的表達式def.x可用于訪問有效質量me和mh。

通過符號def.x使用材料定義中的空間因變量Al_frac。

當訪問物理場設置中的材料屬性時，可以利用前綴material。以下方的截圖為例，它利用表達式material.def.x來查找符號x。前文截圖顯示另一個示例，它利用表達式material.def.me訪問電子有效質量。

使用前綴material訪問物理場設置中的材料屬性。

建立曲線坐標

如前文所述，（在通用幾何的內置變量x、y和 z的簡單表達式不可行的情況下）我們可以利用曲線坐標 接口沿電場線與隧穿邊界建立坐標。此模型幾何是一個簡單的矩形（見 Ref. 1 中的圖 2b），電場線和隧穿邊界坐標簡單地表示為 x 和 y。不過為了進行演示，我們仍然在此模型中使用曲線坐標 接口。如下方截圖所示，我們在“模型開發器”中創建了兩個包含擴散方法 選項的曲線坐標 接口，一個用于電場線，另一個用于隧穿邊界。

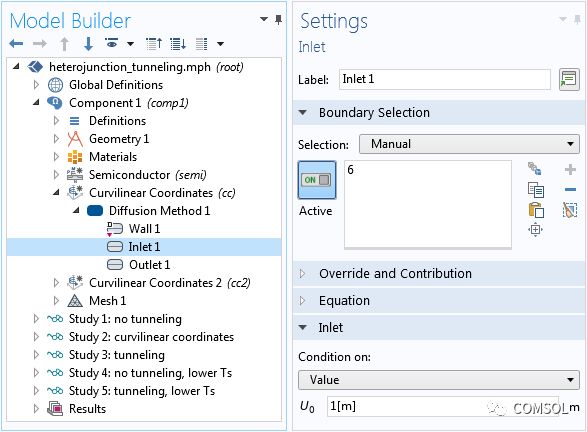
入口邊界的設置窗口。

將入口和出口邊界置于在勢壘域的另一側，這樣可以使解沿期望坐標發生變化。兩個曲線坐標接口的解如下圖所示。

兩個曲線坐標 接口的解。垂直等值線是電場線的坐標，水平等值線是隧穿邊界的坐標。

在此示例中，域 2 恰好覆蓋了感興趣區域，順勢對勢壘進行線積分。通常情況下，我們可以使用幾何內的不同邊界來定義感興趣區域，這些邊界可能與材料邊界重合，也可能不重合。

對于任意幾何，曲線坐標 接口的解也許與電場線坐標不完全重合。不過，它為我們提供了良好的近似，并省去了通過數值方式搜索場線的麻煩。

上圖中的解可用于定義 WKB 隧穿特征的坐標變量。下方截圖顯示了變量定義，前文截圖顯示了 WKB 特征的設置。

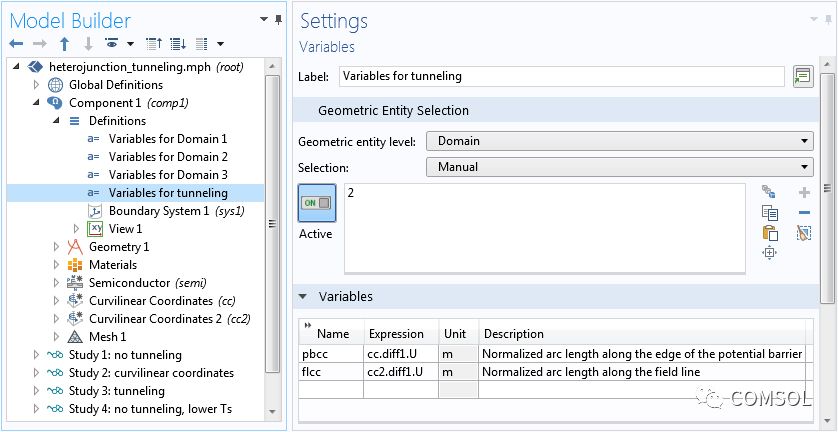
設置窗口顯示隧穿變量的定義。

模擬隧穿效應的其他物理場設置

由于隧穿效應對勢壘的形狀高度敏感，所以我們改用有限元準費米能級公式。考慮到因變量在每個網格單元內均為常數，所以缺省的有限體積公式需要更加精細的網格。

我們在模型樹中建立兩個異質結邊界條件，借此計算與比較包含與不包含隧穿效應的結果。

求解漸變異質結模型

該模型分階段進行求解。“研究 1”計算了無隧穿效應的情況。因為曲線坐標在整個模型中不變，所以“研究 2”僅進行一次求解。

“研究 3”求解了包含隧穿效應的情況，而且只包含半導體物理場。為了提供良好的初始條件，我們使求解變量的初始值 指向“研究 1”的解。由于隧穿特征所需的曲線坐標 接口未包含在研究步驟中，所以我們使不求解的變量值 指向“研究 2”中的解，從而對曲線坐標進行定義。下方截圖顯示了相關設置。

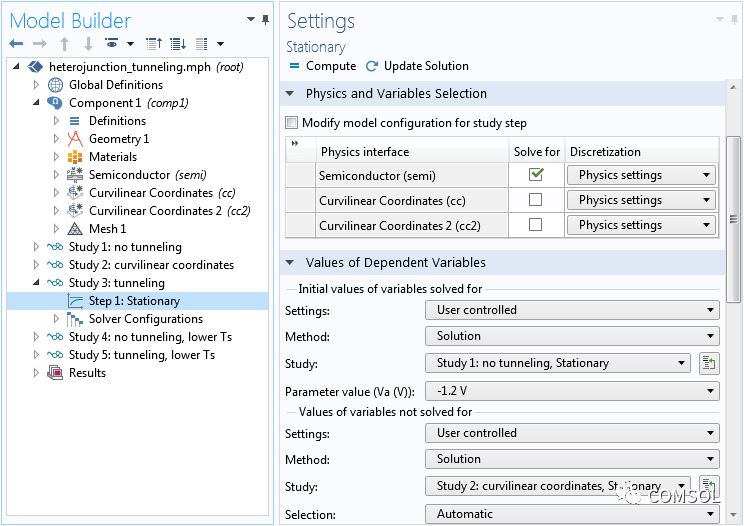
研究設置。注意求解變量的初始值和不求解的變量值使用了不同的研究。

另外兩項研究采用了相似的求解變量的初始值 和不求解的變量值 設置，主要計算低溫下的情況。對于非線性方程系統，我們需要為輔助掃描建立一個良好的初始條件。我們發現，在溫度較低的情況下，如果對 I-V 曲線從低電壓掃描到高電壓，收斂會更加容易。

比較仿真結果與參考文獻

下圖比較了溫度為 300 K 時，有無隧穿效應分別對應的電流密度與電壓（J-V）曲線。結果與 Ref. 1 中的圖 12 很好地吻合。

比較有和沒有隧穿效應情況下的 J-V 曲線。

為了解釋勢壘寬度對隧穿電流大小的影響，文獻圖 13 比較了兩個偏置電壓下的導帶結構示意圖和電子準費米能級。我們的模型準確地還原了相關數據，如下所示。

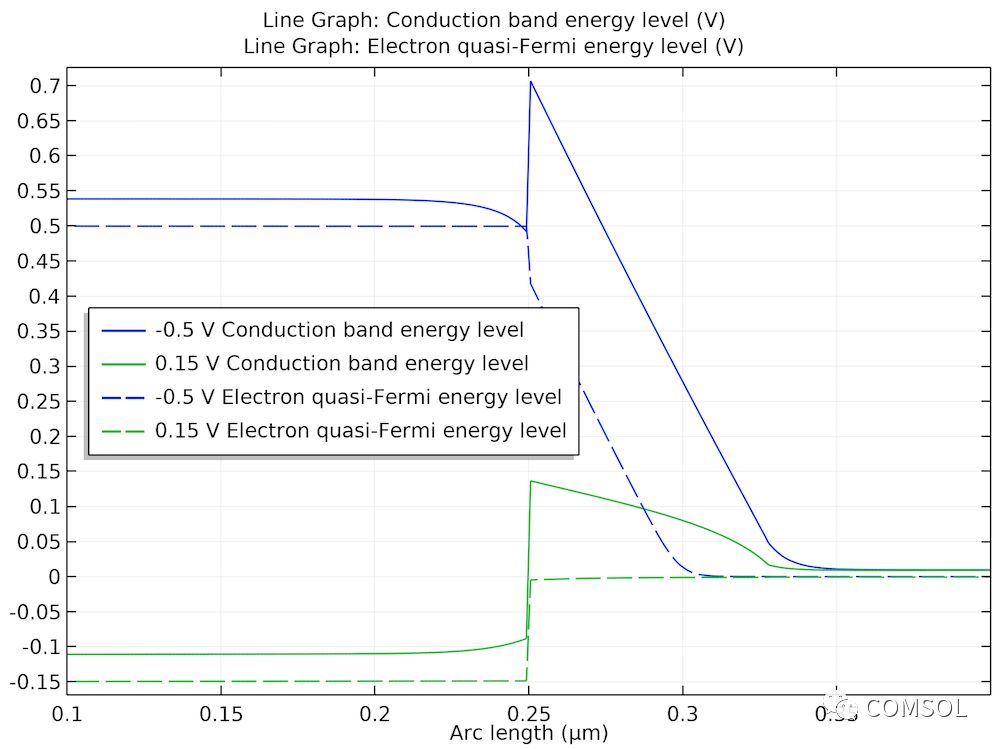
兩個偏置電壓下的導帶圖說明了勢壘寬度對隧穿效應產生的影響。

最后，下圖表明不同溫度下的 J-V 模擬曲線與文獻的圖 14 基本一致。

不同溫度下的 J-V 曲線。

結語

在本篇博客文章中，我們利用漸變異質結基準模型演示了 WKB 特征，并介紹了如何創建用戶定義的三元材料屬性。我們討論了在研究設置中定義求解變量的初始值 和不求解的變量值 的基本技巧，這些技巧可應用于很多建模情景。我們希望您會將這些功能與技巧應用到仿真工作中。

如希望親手嘗試“異質結隧穿”模型，請單擊下方按鈕跳轉至“案例下載”頁面。登錄 COMSOL Access 帳戶后，您可以下載此示例的文檔，如果您擁有有效的軟件許可證，還可以下載 MPH 文件。