在此之前，我們介紹過用于自動(dòng)微分的 TensorFlow API - 自動(dòng)微分，優(yōu)化機(jī)器學(xué)習(xí)模型的關(guān)鍵技術(shù)，這是機(jī)器學(xué)習(xí)的基本構(gòu)建塊。在今天的教程中，我們將使用先前教程中介紹的 TensorFlow 基礎(chǔ)來進(jìn)行一些簡單的機(jī)器學(xué)習(xí)。

TensorFlow 還包括一個(gè)更高級(jí)別的神經(jīng)網(wǎng)絡(luò) API（tf.keras），它提供了有用的抽象來減少樣板。我們強(qiáng)烈建議那些使用神經(jīng)網(wǎng)絡(luò)的人使用更高級(jí)別的 API。但是，在這個(gè)簡短的教程中我們將從神經(jīng)網(wǎng)絡(luò)訓(xùn)練的基本原理來建立一個(gè)堅(jiān)實(shí)的基礎(chǔ)。

設(shè)置

import tensorflow as tftf.enable_eager_execution()

變量

TensorFlow 中的張量是不可變的無狀態(tài)對(duì)象。然而，機(jī)器學(xué)習(xí)模型需要具有可變的狀態(tài)：隨著模型的訓(xùn)練，計(jì)算預(yù)測的相同代碼應(yīng)該隨著時(shí)間的推移而表現(xiàn)不同（希望具有較低的損失！）。要表示在計(jì)算過程中需要改變的狀態(tài)，事實(shí)上您可以選擇依賴 Python 這種有狀態(tài)的編程語言：

# Using python statex = tf.zeros([10, 10])x += 2 # This is equivalent to x = x + 2, which does not mutate the original # value of xprint(x)

tf.Tensor（[[2。2. 2. 2. 2. 2. 2. 2. 2. 2.] [2。2. 2. 2. 2. 2. 2. 2. 2. 2.] [2。2. 2. 2. 2. 2. 2. 2. 2. 2.] [2。2. 2. 2. 2. 2. 2. 2. 2. 2.] [2。2. 2. 2. 2. 2. 2. 2. 2. 2.] [2。2. 2. 2. 2. 2. 2. 2. 2. 2.] [2。2. 2. 2. 2. 2. 2. 2. 2. 2.] [2。2. 2. 2. 2. 2. 2. 2. 2. 2.] [2。2. 2. 2. 2. 2. 2. 2. 2. 2.] [2。2. 2. 2. 2. 2. 2. 2. 2. 2.]]，shape =（10,10），dtype = float32）

但是，TensorFlow 內(nèi)置了有狀態(tài)操作，這些操作通常比您所用的低級(jí) Python 表示更易于使用。例如，為了表示模型中的權(quán)重，使用 TensorFlow 變量通常是方便有效的。

變量是一個(gè)存儲(chǔ)值的對(duì)象，當(dāng)在 TensorFlow 計(jì)算中使用時(shí)，它將隱式地從該存儲(chǔ)值中讀取。有些操作（如：tf.assign_sub，tf.scatter_update 等）會(huì)操縱存儲(chǔ)在 TensorFlow 變量中的值。

v = tf.Variable(1.0)assert v.numpy() == 1.0# Re-assign the valuev.assign(3.0)assert v.numpy() == 3.0# Use `v` in a TensorFlow operation like tf.square() and reassignv.assign(tf.square(v))assert v.numpy() == 9.0

使用變量的計(jì)算在計(jì)算梯度時(shí)自動(dòng)跟蹤。對(duì)于表示嵌入式的變量，TensorFlow 默認(rèn)會(huì)進(jìn)行稀疏更新，這樣可以提高計(jì)算效率和內(nèi)存效率。

使用變量也是一種快速讓代碼的讀者知道這段狀態(tài)是可變的方法。

示例：擬合線性模型

現(xiàn)在讓我們把目前掌握的幾個(gè)概念 — 張量、梯度帶、變量 — 應(yīng)用到構(gòu)建和訓(xùn)練一個(gè)簡單模型中去。這通常涉及幾個(gè)步驟：

1.定義模型。

2.定義損失函數(shù)。

3.獲取訓(xùn)練數(shù)據(jù)。

4.運(yùn)行訓(xùn)練數(shù)據(jù)并使用 “優(yōu)化器” 調(diào)整變量以匹配數(shù)據(jù)。

在本教程中，我們將介紹一個(gè)簡單線性模型的簡單示例：f(x) = x * W + b，它有兩個(gè)變量 —W 和 b。此外，我們將綜合數(shù)據(jù)，以便訓(xùn)練好的模型具有 W = 3.0 和 b = 2.0。

定義模型

讓我們定義一個(gè)簡單的類來封裝變量和計(jì)算。

class Model(object): def __init__(self): # Initialize variable to (5.0, 0.0) # In practice, these should be initialized to random values. self.W = tf.Variable(5.0) self.b = tf.Variable(0.0) def __call__(self, x): return self.W * x + self.b model = Model()assert model(3.0).numpy() == 15.0

定義損失函數(shù)

損失函數(shù)測量給定輸入的模型輸出與期望輸出的匹配程度。讓我們使用標(biāo)準(zhǔn)的 L2 損失。

def loss(predicted_y, desired_y): return tf.reduce_mean(tf.square(predicted_y - desired_y))

獲取訓(xùn)練數(shù)據(jù)

讓我們用一些噪音（noise）合成訓(xùn)練數(shù)據(jù)。

TRUE_W = 3.0TRUE_b = 2.0NUM_EXAMPLES = 1000inputs = tf.random_normal(shape=[NUM_EXAMPLES])noise = tf.random_normal(shape=[NUM_EXAMPLES])outputs = inputs * TRUE_W + TRUE_b + noise

在我們訓(xùn)練模型之前，讓我們想象一下模型現(xiàn)在的位置。我們將用紅色繪制模型的預(yù)測，用藍(lán)色繪制訓(xùn)練數(shù)據(jù)。

import matplotlib.pyplot as pltplt.scatter(inputs, outputs, c='b')plt.scatter(inputs, model(inputs), c='r')plt.show()print('Current loss: '),print(loss(model(inputs), outputs).numpy())

Current loss:

7.92897

定義訓(xùn)練循環(huán)

我們現(xiàn)在有了網(wǎng)絡(luò)和培訓(xùn)數(shù)據(jù)。我們來訓(xùn)練一下，使用訓(xùn)練數(shù)據(jù)更新模型的變量 ( W 和 b)，以便使用梯度下降減少損失。在 tf.train.Optimizer 實(shí)現(xiàn)中有許多梯度下降方案的變體。我們強(qiáng)烈建議使用這種實(shí)現(xiàn)，但本著從基本原理出發(fā)的精神，在這個(gè)特定的例子中，我們將自己實(shí)現(xiàn)基本的數(shù)學(xué)。

def train(model, inputs, outputs, learning_rate): with tf.GradientTape() as t: current_loss = loss(model(inputs), outputs) dW, db = t.gradient(current_loss, [model.W, model.b]) model.W.assign_sub(learning_rate * dW) model.b.assign_sub(learning_rate * db)

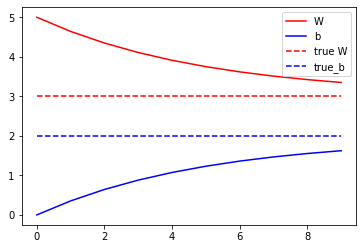
最后，讓我們反復(fù)運(yùn)行訓(xùn)練數(shù)據(jù)，看看 W 和 b 是如何發(fā)展的。

model = Model()# Collect the history of W-values and b-values to plot laterWs, bs = [], []epochs = range(10)for epoch in epochs: Ws.append(model.W.numpy()) bs.append(model.b.numpy()) current_loss = loss(model(inputs), outputs) train(model, inputs, outputs, learning_rate=0.1) print('Epoch %2d: W=%1.2f b=%1.2f, loss=%2.5f' % (epoch, Ws[-1], bs[-1], current_loss))# Let's plot it allplt.plot(epochs, Ws, 'r', epochs, bs, 'b')plt.plot([TRUE_W] * len(epochs), 'r--', [TRUE_b] * len(epochs), 'b--')plt.legend(['W', 'b', 'true W', 'true_b'])plt.show()

Epoch 0: W=5.00 b=0.00, loss=7.92897Epoch 1: W=4.64 b=0.35, loss=5.61977Epoch 2: W=4.35 b=0.64, loss=4.07488Epoch 3: W=4.11 b=0.88, loss=3.04133Epoch 4: W=3.91 b=1.07, loss=2.34987Epoch 5: W=3.75 b=1.23, loss=1.88727Epoch 6: W=3.62 b=1.36, loss=1.57779Epoch 7: W=3.51 b=1.47, loss=1.37073Epoch 8: W=3.42 b=1.55, loss=1.23221Epoch 9: W=3.35 b=1.62, loss=1.13954

下一步

在本教程中，我們介紹了變量 Variables，使用了到目前為止討論的 TensorFlow 基本原理構(gòu)建并訓(xùn)練了一個(gè)簡單的線性模型。

從理論上講，這幾乎是您使用 TensorFlow 進(jìn)行機(jī)器學(xué)習(xí)研究所需要的全部內(nèi)容。在實(shí)踐中，特別是對(duì)于神經(jīng)網(wǎng)絡(luò)，更高級(jí)別的 APItf.keras 會(huì)更方便，因?yàn)樗峁└呒?jí)別的構(gòu)建塊（稱為 “層”），保存和恢復(fù)狀態(tài)的實(shí)用程序，一套損失函數(shù)，一套優(yōu)化策略等等。