在從事數(shù)據(jù)科學(xué)工作的時(shí)候，經(jīng)常會(huì)遇到為具體問題選擇最合適算法的問題。雖然有很多有關(guān)機(jī)器學(xué)習(xí)算法的文章詳細(xì)介紹了相關(guān)的算法，但要做出最合適的選擇依然非常困難。

在這篇文章中，我將對一些基本概念給出簡要的介紹，對不同任務(wù)中使用不同類型的機(jī)器學(xué)習(xí)算法給出一點(diǎn)建議。在文章的最后，我將對這些算法進(jìn)行總結(jié)。

首先，你應(yīng)該能區(qū)分以下四種機(jī)器學(xué)習(xí)任務(wù)：

監(jiān)督學(xué)習(xí)

無監(jiān)督學(xué)習(xí)

半監(jiān)督學(xué)習(xí)

強(qiáng)化學(xué)習(xí)

監(jiān)督學(xué)習(xí)

監(jiān)督學(xué)習(xí)是從標(biāo)記的訓(xùn)練數(shù)據(jù)中推斷出某個(gè)功能。通過擬合標(biāo)注的訓(xùn)練集，找到最優(yōu)的模型參數(shù)來預(yù)測其他對象（測試集）上的未知標(biāo)簽。如果標(biāo)簽是一個(gè)實(shí)數(shù)，我們稱之為回歸。如果標(biāo)簽來自有限數(shù)量的值，這些值是無序的，那么稱之為分類。

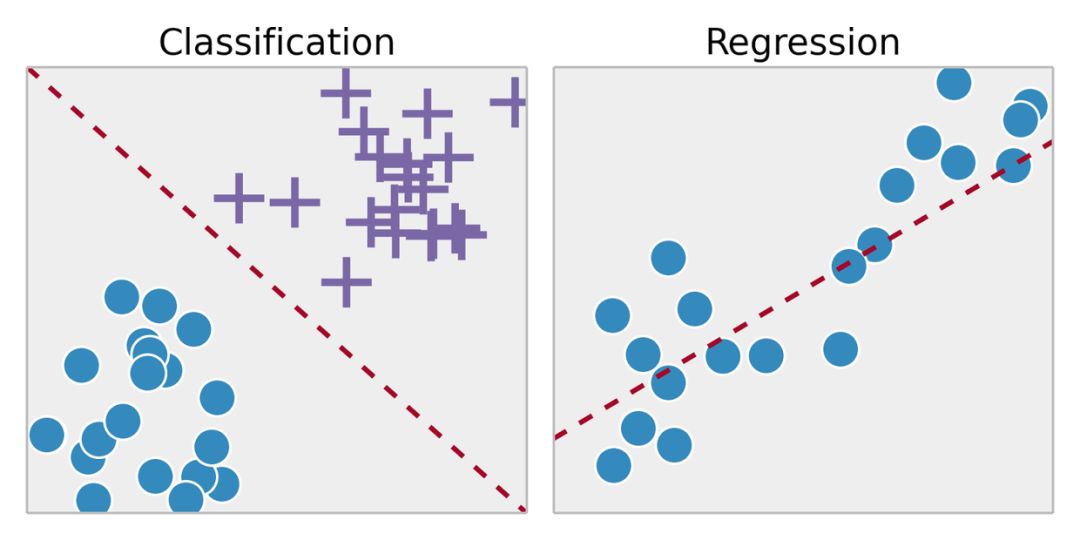
無監(jiān)督學(xué)習(xí)

在無監(jiān)督學(xué)習(xí)中，我們對于物體知道的信息比較少，特別是訓(xùn)練集沒有做過標(biāo)記。那現(xiàn)在的目標(biāo)是什么呢？觀察對象之間的相似性，并將它們劃分到不同的群組中。某些對象可能與其他群組中的對象都有很大的區(qū)別，那么我們就認(rèn)為這些對象是異常的。

半監(jiān)督學(xué)習(xí)

半監(jiān)督學(xué)習(xí)包括了前面描述的兩個(gè)問題：同時(shí)使用標(biāo)記和未標(biāo)記的數(shù)據(jù)。對于那些無法標(biāo)注所有數(shù)據(jù)的人來說，這是一個(gè)很好的方法。該方法能夠顯著提高準(zhǔn)確性，因?yàn)樵谑褂糜?xùn)練集中未標(biāo)記數(shù)據(jù)的同時(shí)，還能使用少量帶有標(biāo)記的數(shù)據(jù)。

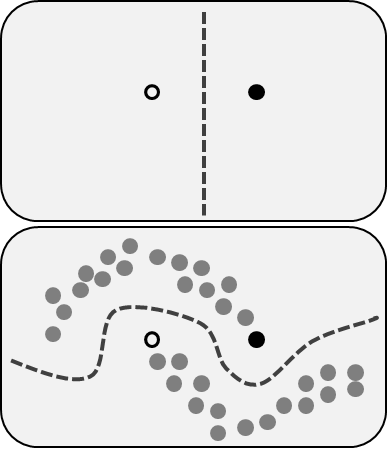
強(qiáng)化學(xué)習(xí)

強(qiáng)化學(xué)習(xí)跟上面提到的方法不太一樣，因?yàn)樵谶@里并沒有標(biāo)記或未標(biāo)記的數(shù)據(jù)集。強(qiáng)化學(xué)習(xí)涉及到軟件代理應(yīng)該如何在某些環(huán)境中采取行動(dòng)來最大化累積獎(jiǎng)勵(lì)。

想象一下，你是一個(gè)在陌生環(huán)境中的機(jī)器人，你可以執(zhí)行一些動(dòng)作，并從中獲得獎(jiǎng)勵(lì)。在每執(zhí)行一個(gè)動(dòng)作之后，你的行為會(huì)變得越來越復(fù)雜越來越聰明，也就是說 ，你正在訓(xùn)練自己在執(zhí)行每一個(gè)動(dòng)作之后讓自己表現(xiàn)得更為有效。在生物學(xué)中，這被稱為適應(yīng)自然環(huán)境。

常用的機(jī)器學(xué)習(xí)算法

現(xiàn)在，我們對機(jī)器學(xué)習(xí)的類型有了一定的了解，下面，我們來看一下最流行的算法及其在現(xiàn)實(shí)生活中的應(yīng)用。

線性回歸和線性分類器

這些可能是機(jī)器學(xué)習(xí)中最簡單的算法了。假設(shè)有對象（矩陣A）的特征x1，... xn和標(biāo)簽（向量B）。我們的目標(biāo)是根據(jù)某些損失函數(shù)（例如MSE或MAE）找到最優(yōu)權(quán)重w1，... wn和這些特征的偏差。 在使用MSE的情況下，有一個(gè)來自最小二乘法的數(shù)學(xué)公式：

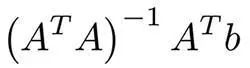
在實(shí)踐中，使用梯度下降來進(jìn)行優(yōu)化則更為容易，計(jì)算上更有效率。盡管這個(gè)算法很簡單，但是在存在成千上萬個(gè)特征的時(shí)候，這個(gè)方法依然能夠表現(xiàn)良好。更復(fù)雜的算法可能會(huì)遇到過擬合特征或者是沒有足夠大的數(shù)據(jù)集的問題，而線性回歸則是一個(gè)不錯(cuò)的選擇。

為了防止過擬合，可使用像lasso和ridge這樣的規(guī)則化技術(shù)。其主要思路是分別把權(quán)重總和以及權(quán)重平方的總和加到損失函數(shù)中。

邏輯回歸

邏輯回歸執(zhí)行的是二元分類，所以輸出的標(biāo)簽是二元的。給定輸入特征向量x，定義P(y=1|x)為輸出y等于1時(shí)的條件概率。系數(shù)w是模型要學(xué)習(xí)的權(quán)重。

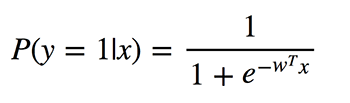
由于該算法需要計(jì)算每個(gè)類別的歸屬概率，因此應(yīng)該考慮概率與0或1的差異程度，并像在線性回歸中一樣對所有對象取平均值。這種損失函數(shù)是交叉熵的平均值：

邏輯回歸有什么好處呢？它采用了線性組合的特征，并對其應(yīng)用非線性函數(shù)（sigmoid），所以它是一個(gè)非常小的神經(jīng)網(wǎng)絡(luò)實(shí)例！

決策樹

另一個(gè)比較流行、并且容易理解的算法是決策樹。它的圖形能讓你看到你自己的想法，它的引擎有一個(gè)系統(tǒng)的、有記錄的思考過程。

這個(gè)算法很簡單。在每個(gè)節(jié)點(diǎn)中，我們選擇所有特征和所有可能的分割點(diǎn)之間的最佳分割。選擇每個(gè)分割以最大化某些功能。在分類樹中使用交叉熵和基尼指數(shù)。在回歸樹中，最小化該區(qū)域中的點(diǎn)的目標(biāo)值的預(yù)測變量與分配給它的點(diǎn)之間的平方誤差的總和。

算法會(huì)在每個(gè)節(jié)點(diǎn)上遞歸地完成這個(gè)過程，直到滿足停止條件為止。

K-means

有的時(shí)候你并不知道標(biāo)簽，而目標(biāo)是根據(jù)對象的特征來分配標(biāo)簽。這被稱為集聚化任務(wù)。

假設(shè)要把所有的數(shù)據(jù)對象分成k個(gè)簇，則需要從數(shù)據(jù)中隨機(jī)選擇k個(gè)點(diǎn)，并將它們命名為簇的中心。其他對象的簇由最近的簇中心定義。然后，聚類的中心會(huì)被轉(zhuǎn)換并重復(fù)該過程直到收斂。

雖然這個(gè)技術(shù)非常不錯(cuò)，但它仍然有一些缺點(diǎn)。首先，我們并不知道簇的數(shù)量。其次，結(jié)果依賴開始時(shí)隨機(jī)選擇的那個(gè)點(diǎn)，算法無法保證我們能夠?qū)崿F(xiàn)功能的全局最小值。

主成分分析（PCA）

昨晚或者最近的幾個(gè)小時(shí)里你有沒有在準(zhǔn)備考試？你無法記住所有的信息，但是想要在可用的時(shí)間內(nèi)最大限度地記住信息，例如，首先學(xué)習(xí)考試中經(jīng)常出現(xiàn)的定理等等。

主成分分析基于類似的思想。該算法提供了降維的功能。有時(shí)，你有很多的特征，并且彼此之間強(qiáng)相關(guān)，模型可以很容易地適應(yīng)大量的數(shù)據(jù)。然后，你可以應(yīng)用PCA。

你應(yīng)該計(jì)算某些向量上的投影，以使數(shù)據(jù)的方差最大化，并盡可能少地丟失信息。而這些向量是來自數(shù)據(jù)集特征的相關(guān)矩陣的特征向量。

算法的內(nèi)容現(xiàn)在已經(jīng)很清楚了：

計(jì)算特征列的相關(guān)矩陣，找出該矩陣的特征向量。

將這些多維向量計(jì)算出來，并計(jì)算所有特征的投影。

新特征是投影中的坐標(biāo)，其數(shù)量取決于投影的特征向量的數(shù)量。

神經(jīng)網(wǎng)絡(luò)

在上文講到邏輯回歸的時(shí)候，就已經(jīng)提到了神經(jīng)網(wǎng)絡(luò)。在一些具體的任務(wù)中，有很多不同的體系結(jié)構(gòu)都非常有價(jià)值。而神經(jīng)網(wǎng)絡(luò)更多的時(shí)候是一系列的層或組件，它們之間存在線性連接并遵循非線性。

如果你正在處理圖像，那么卷積深度神經(jīng)網(wǎng)絡(luò)能展現(xiàn)出不錯(cuò)的結(jié)果。而非線性則通過卷積層和匯聚層表現(xiàn)出來，它能夠捕捉圖像的特征。

要處理文本和序列，最好選擇遞歸神經(jīng)網(wǎng)絡(luò)。 RNN包含了LSTM或GRU模塊，并且能夠數(shù)據(jù)一同使用。也許，最有名的RNN應(yīng)用是機(jī)器翻譯吧。

結(jié)論

我希望能向大家解釋最常用的機(jī)器學(xué)習(xí)算法，并就針對具體問題如何選擇機(jī)器學(xué)習(xí)算法提供建議。為了能讓你更輕松的掌握這些內(nèi)容，我準(zhǔn)備了下面這個(gè)總結(jié)。

線性回歸和線性分類器。盡管看起來簡單，但當(dāng)其他算法在大量特征上遇到過擬合的問題時(shí)，它的優(yōu)勢就表現(xiàn)出來了。

Logistic回歸是最簡單的非線性分類器，具有二元分類的參數(shù)和非線性函數(shù)（S形）的線性組合。

決策樹通常與人類的決策過程相似，并且易于解釋。但它們最常用于隨機(jī)森林或梯度增強(qiáng)這樣的組合中。

K-means是一個(gè)更原始、但又非常容易理解的算法。

PCA是降低信息損失最少的特征空間維度的絕佳選擇。

神經(jīng)網(wǎng)絡(luò)是機(jī)器學(xué)習(xí)算法的新武器，可以應(yīng)用于許多任務(wù)，但其訓(xùn)練的計(jì)算復(fù)雜度相當(dāng)大。