棱柱形狀的天然水晶、立方體一樣的螢石、柱狀的天然石膏、一片一片分層的天然云母,這些礦石都有著獨特的形狀結(jié)構(gòu),散發(fā)著璀璨奪目的魅力。那么它們列隊整齊的背后又有什么物理學小秘密呢?且聽中國科學院大學博士生導師、中國科學院物理所研究員曹則賢教授為君娓娓道來。
摘要
晶體具有規(guī)則的外形,來自內(nèi)部原子的規(guī)則排列。晶體具有最小的重復單元,是由最小重復單元在三維空間堆積起來的,即晶體具有平移對稱性。對稱性可以用群這個數(shù)學概念來表征。平移對稱性限制了晶體重復單元只有n=1,2,3,4,6次轉(zhuǎn)軸,因此晶體只有32種點群(單胞的對稱性)。32種點群同三維空間中平移操作的組合,決定了晶體只有230種空間群。不管有多少種具體的晶體,按照對稱性分類只有230種。二維情形下,n=1,2,3,4,6次轉(zhuǎn)軸加上鏡面反映只能得到10種點群;10種點群與二維空間中的平移操作組合,只能得到17種二維空間群。遠在人類有群論知識之前,許多文明都認識到了二維晶體只有17種對稱性,反映在二維裝飾圖案,比如窗欞的設計上。
01
晶體
自然中存在許多固體,其中一些固體具有規(guī)則、美觀的外形,比如見于火山口的金剛石、水晶和硫磺等,它們被稱為晶體。 晶體具有規(guī)則的外形,如果仔細觀察,會發(fā)現(xiàn)其小面之間成恒定的夾角,與晶體大小無關(圖1)。
圖1. 天然晶體:金剛石、水晶和硫磺
打碎的晶體小塊中能看到許多相似的形狀,這讓人們猜測晶體具有一個最小的幾何單元,稱為單胞(unit cell), 晶體是單胞在三維空間中堆砌而成的,類似紙箱子堆滿倉庫。平行六面體(特例為正方體),開爾文爵士的截角八面體,都能充滿整個空間(圖2)。由此而來的一個認識是,晶體具有平移對稱性,平移對稱性又決定了晶體中允許存在的轉(zhuǎn)動只有n=1,2,3,4,6次轉(zhuǎn)動這五種可能,這被稱為晶體學限制定理。作為數(shù)學的表現(xiàn)是,描述晶體轉(zhuǎn)動的矩陣的跡(trace of matrix),必為整數(shù)。
這個晶體學限制定理,還有個簡單證明。考慮到晶體是原子層堆垛而成,故而只需考慮一個平面上的排列方式所允許的轉(zhuǎn)動。平面有兩個獨立方向,這注定了平行四邊形是平面上的單胞。畫兩組成一定夾角的線簇,可看到是平行四邊形的單胞鋪滿整個平面。任意改變平行四邊形的邊長比和夾角,可看出這個平面鋪排的花樣會出現(xiàn)哪些轉(zhuǎn)動對稱性。任意的邊長比和夾角,沒有轉(zhuǎn)動對稱性,或者只有n=1次的轉(zhuǎn)軸;夾角90°,邊長不等,對應n=2次的轉(zhuǎn)軸;夾角90°,邊長相等,對應n=4次的轉(zhuǎn)軸;夾角60°,邊長相等,對應n=6(3)次的轉(zhuǎn)軸。
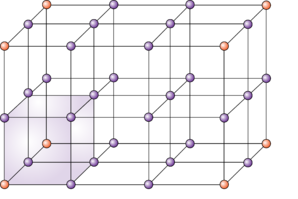
圖2. 正方體和截面八面體都能充滿整個空間
平移對稱性決定了晶體中只有n=1,2,3,4,6次這五種轉(zhuǎn)動,這限制了晶體單胞所能具有的對稱性(點群),也就限制了單胞對稱性與平移對稱性的組合(空間群)。實際的三維晶體只有32種點群,230種空間群。為了理解的方便,本篇多借助二維情形展開相關討論,而二維晶體只有10種點群,17種空間群。而且二維的空間群又叫墻紙群(wallpaper group), 會感覺特別的親切!
02
對稱性與群
對稱性操作可用群的概念描述。群的概念是研究幾何和代數(shù)方程解的時候提出來的。
若一組操作(operation,動作) 滿足如下四個條件:
1. 有一個單元操作 I (操作以后對象不變,或者是什么也沒發(fā)生);
2. 兩個操作接連完成的效果等于這個集合里某個單一操作的效果(用群論語言,G×G∈G)
3. 操作滿足結(jié)合律 (用群論語言,gi(gjgk)=(gigj)gk)
4. 每一個操作都有逆操作 (用群論語言,總存在 gj=gi-1,gigj=gjgi=I)
這一組動作就構(gòu)成一個群(group)。 其實,群就是一種特殊的集合,其元素間定義了滿足結(jié)合律的乘法,且按照這個乘法每一個元素還都有逆。對稱性操作就滿足群的定義。注意,一個群元素可以表示為一個數(shù)學對象,比如矩陣,因此群是物理學研究的重要工具。
圖3. C5對稱的雞蛋花和D3對稱的三葉草
舉例來說,圖3左圖為雞蛋花,五瓣,繞中心軸轉(zhuǎn)2π/5看不出曾有過轉(zhuǎn)動。我們說(理想的)雞蛋花具有C5對稱性,其對稱群為C5群。關于雞蛋花的對稱操作有轉(zhuǎn)動0,2π/5,4π/5,6π/5和8π/5角這五種可能,可以驗證它們滿足群的定義。 又比如圖3右圖中的三葉草,它的對稱性和正三角形是一樣,繞中心軸轉(zhuǎn)2π/3角相對于過頂點的中線作鏡面反映(σ-操作),都看不出變化。(理想的)三葉草具有D3對稱性,其對稱群為D3群。關于三葉草的對稱操作有轉(zhuǎn)動0,2π/3,4π/3和鏡面反映σ1,σ2,σ3這六種可能,可以驗證它們滿足群的定義。
03
二維晶體的點群與空間群
二維空間里,轉(zhuǎn)動只有n=1,2,3,4,6次轉(zhuǎn)軸五種可能,這構(gòu)成了C1,C2,C3,C4,C6五種點群,添加鏡面反映(其實是線反映)也各只有一種可能, ? , 這構(gòu)成了D1,D2,D3,D4,D6五種點群。這樣,二維點群總共就這么十種。此處使用Sch?flies記號,下同。
? , 這構(gòu)成了D1,D2,D3,D4,D6五種點群。這樣,二維點群總共就這么十種。此處使用Sch?flies記號,下同。
已知了二維點群,使其同平移對稱性結(jié)合(有時有多與一種的方式),可以構(gòu)造出二維空間群。用通俗的話來說,設想你設計平面裝飾圖案,你先在平面上劃格子(lattice), 格子具有某種平移對稱性(平移群),然后設計重復單元(motif),重復單元具有某種轉(zhuǎn)動加鏡面反映的對稱性(點群)。 若重復單元與格子相匹配,就可以在每個格點上放上那個重復單元,就湊成了整幅具有某種特定對稱性(空間群)的圖案。二維空間群(墻紙群)是建筑、服裝、繪畫、材料、物理等專業(yè)工人的必備知識。
現(xiàn)在看二維點群與二維格子構(gòu)成二維空間群的具體情況。先介紹要用到的術語,C是cyclic (循環(huán)的、轉(zhuǎn)圈的)的首字母,D是dihedral (二面的)的首字母,p是primitive (初級的)的首字母,c是centered (帶心的) 的首字母,m代表mirror (鏡面),g代表 glide (滑移面,經(jīng)這個面反映后,還移動一段距離)。空間群的記號會大致告訴你晶體的對稱性特征,比如pmg 是初級晶格+鏡面+滑移面,cmm是面心晶格(單胞是帶心的長方形)+垂直方向上的鏡面。二維空間群共17種可能,排列如下:
1) 點群C1,C2,C3,C4,C6分別對應空間群 p1, p2, p3, p4,p6;
2) 點群D1對應空間群 pm, pg, cm;
3) 點群D2對應空間群 pmm, pmg, pgg, cmm;
4) 點群D3對應空間群P31m, P3m1;
5) 點群D4對應空間群 p4m, p4g;
6) 點群D6對應空間群p6m.




圖4.空間群為pm,p4m,p31m,p6m的二維圖片
重復單元的對稱性與晶格對稱性的匹配問題,高對稱性的重復單元要求高對稱性的格子,其中,點群C3,C6,D3,D6要求六角格子,其單胞是夾角60°的菱形;C4,D4點群,要求正方格子。為了加深理解,圖4 中給出了具有空間群的花樣, 讀者可自己試試找出相應的重復單元和單胞。二維空間群只有17 種已知有幾個世紀了,它的別名——墻紙群可資為證。但其證明,或者說基于數(shù)學知識的列舉,要等到1891年由菲德羅夫(Евгра?ф Степа?нович Фёдоров, 1853-1919)才給出。
04
三維晶體的點群與空間群
三維空間依然只有平面型的轉(zhuǎn)動,即只有n=1,2,3,4,6次五種轉(zhuǎn)動,但多了一個維度,因此就擴大了轉(zhuǎn)動與鏡面反映組合的可能性。轉(zhuǎn)軸除了C 和D 的區(qū)別外, 要加入鏡面,可能是v(vertical, 豎直的,鏡面過轉(zhuǎn)軸),也可能是d(diagonal, 對角的,鏡面過轉(zhuǎn)軸) ,還可能是h(horizontal, 水平的,鏡面垂直于轉(zhuǎn)軸 ) 。 此外,還有轉(zhuǎn)動與鏡面反映的組合S(Spiegel,德語,鏡子),以及高對稱的T(tetrahedron, 正四面體)和O(octahedron, 正八面體)。
三維點群可列舉如下,C1,C2,C3,C4,C6共五種,加h得Cnh五種,加v得Cnv五種;D1,D2,D3,D4,D6五種,加h得Dnh五種,加d得Dnd五種,共30種。 然而,在三維空間中C1v=C1h,D1=C2,D1h=C2v,D1d=C2h, 而D4d,D6d意味著存在8-次和12-次轉(zhuǎn)軸,是不允許的。排除這6種可能,實際上得到的是24種點群。加上更復雜的組合S2,S4和S6;T, Th,Td;O, Oh, 又有8種,故總共有32種點群。
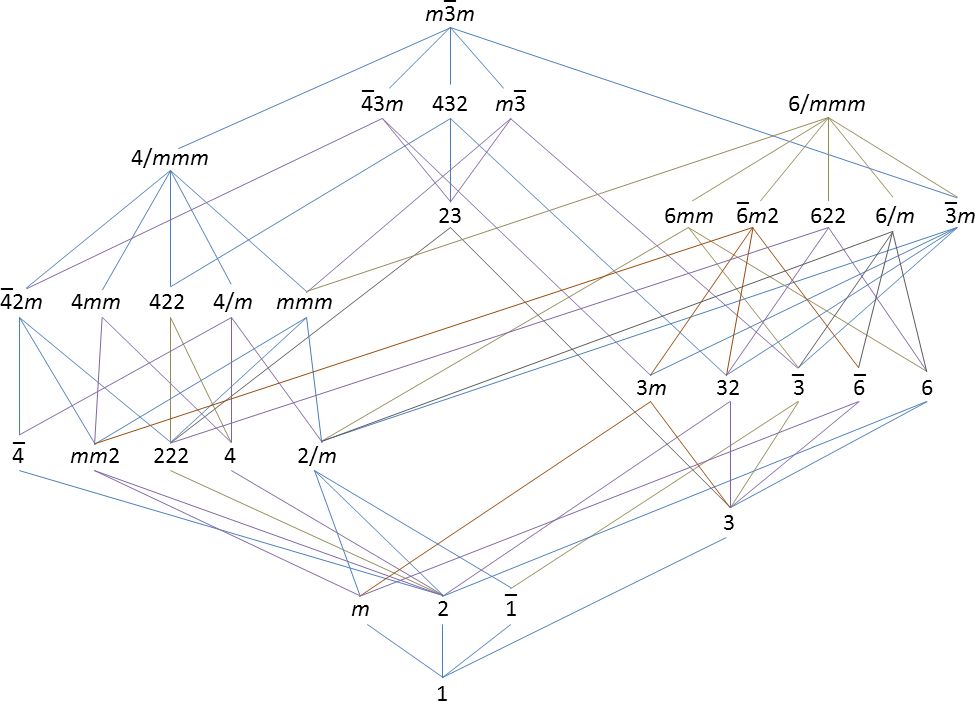
圖5. 32種三維空間點群的關系
(此處使用的是Hermann-Mauguin記號)
這32種點群,對稱性高低不同,其中Oh,O6h,O4h分別占據(jù)最高端,其它低對稱性點群是高對稱性點群的子群,如圖5。32種點群的結(jié)果,是由赫賽爾(Johann Friedrich Christian Hessel, 1796-1872)于1830年推導出來的。
32種點群與三維空間平移對稱性組合,可得到230種空間群(若不同手征的只算一種,是219種)。三維空間群由菲德羅夫和熊夫利斯(Arthur Moritz Sch?nflies,1853-1928)于 1891年獨立地列舉空間群,但各有疏漏。1892年兩人在通訊中互相校正,得到了230種正確的列表。由于內(nèi)容太多,此處不一一列舉了。 有興趣的讀者,尤其是凝聚態(tài)物理類的研究生,請參閱相關專業(yè)書籍。這中間的一個關鍵步驟是,確立了三維空間的格子只有14種, 這是由布拉菲(Auguste Bravais, 1811-1863 )于1850年完成的。
所謂的布拉菲格子,是由那個根據(jù)平移能夠充滿空間的單胞(平行六面體)的形狀加以表征的。布拉菲格子,用其單胞來指代,按照點群對稱性由低到高,分別有三斜晶系/Ci一種,單斜晶系/C2h兩種(外加帶底心的),正交晶系/D2h四種(外加帶底心的, 帶體心的,帶面心的),四方晶系/D4h兩種(外加帶體心的);六角晶系/D3d和/D6h各一種,以及立方晶系/Oh三種(外加帶體心的,帶面心的),如圖6。 各種教科書內(nèi)鮮有排列順序正確的圖示,甚至有把三方晶系和三斜晶系并列的圖解。順便說一句,布拉菲是群論創(chuàng)始人之一伽羅華在巴黎工科學校的同班同學。

圖6. 從上到下按對稱性排列的14種布拉菲格子
05
點群與空間群的再推導
點群與空間群的關系,來自晶體平移對稱性的約束。晶體的平移對稱性宣稱,若在空間某個點r(x,y,z)上有原子,存在三個線性不相關的基矢量 a1,a2,a3,在R=n1a1+n2a2+n3a3+r處(n1,n2,n3是任意整數(shù)),必有原子。但若將該原子放到合適的格點上,公式中的r值, 以基矢量來表示,也只能是有限的幾種可能(與帶心的單胞或滑移面有關)。這個平移對稱性限制了單胞形狀的可能,也限制了點群和空間群的數(shù)目。
從數(shù)學的角度來看,晶體中的變換不改變空間中任一兩點間的距離,因此它必須是取向歐幾里得空間里的等距變換(group of isometries of an oriented Euclidean space)。因為原子是離散的,所以點群、空間群也是分立的(離散的、分立的,discrete)。空間群的一個元素,由(M, D)構(gòu)成, 其作用是等距變換Y=M·X+D,M是個矩陣,M 矩陣形成一個點群;D是個矢量,由點群和點群能匹配的晶格共同決定。考慮到平移對稱性意思是R=n1a1+n2a2+n3a3+r中的n1,n2,n3是任意整數(shù),空間群可以看作是某些整數(shù)域上的變換群。從群論出發(fā),硬推導出三維空間的230種可能,對誰都是挑戰(zhàn)。熊夫利斯的導師可是大數(shù)學家?guī)炷瑺?Ernst Kummer, 1810-1893) 和威爾斯特拉斯(Karl Weierstrass, 1815-1897), 而威爾斯特拉斯可是分析學的奠基人。
2007年,David Hestenes用歐幾里得空間的共形幾何代數(shù)方法給出了二維、三維情形下晶系、點群和空間群的詳細推導。更重要的是,還給出了各個空間群的生成元。不過,追蹤過David Hestenes用幾何代數(shù)重寫整個物理學努力的人太少了。不知道將來是否有有能力對晶體學感興趣的人詳細講解這項工作。
06
多余的話
晶體學群論的工作,是由一批德國和俄羅斯科學家完成的。礦物學發(fā)祥于這兩個國家,相關的數(shù)學這兩個國家的人有能力掌握,因此由他們構(gòu)造晶體群以及考慮更高維格子、更復雜motif之晶體的群(比如色群)就顯得天經(jīng)地義了。他們這些工作追求的是關于物質(zhì)的結(jié)構(gòu)原則,結(jié)構(gòu)原則同樣適用于數(shù)學—結(jié)構(gòu)是數(shù)學的最高原則。Some mathematical structures show up in many different contexts, under many different guises。 推導出完整的空間群是很困難的,從32種點群于1830年由一人推導出來到230種空間群于1891-1892年由兩人才正確推導出來,這其中的難度可以想象。 可惜這些文獻多是德語和俄語的, 尤其那些珍貴的俄語文獻鮮有譯文,現(xiàn)在是更沒有人肯去掌握了。
還有一點難能可貴的是,德國和俄羅斯的科學家和工程師似乎有點傻傻地真心熱愛科學。一個理所當然的結(jié)果是,它們的人工晶體長得非常好。俄羅斯不僅有多種系統(tǒng)的晶體學教科書,他們長晶體也是最棒的。看著俄羅斯人生長的一人多高的硅單晶,令人不由得肅然起敬。
固體物理學教育在吾國已經(jīng)開展多年了。然而,關于晶體結(jié)構(gòu)數(shù)學的介紹,基本上還只停留在固體有32種點群、230空間群這么一句膚淺的介紹上。群論,群表示論,空間群的導出與表示,空間群在計算物理方面的應用,空間群對物質(zhì)物理性質(zhì)的限制,空間群對物質(zhì)刺激-響應行為的限制,這些都應該成為凝聚態(tài)物理類研究生的必備知識。
-
晶體
+關注
關注
2文章
1379瀏覽量
35905 -
矩陣
+關注
關注
0文章
428瀏覽量
34878
原文標題:你以為你真了解晶體?看懂對稱群再說吧
文章出處:【微信號:bdtdsj,微信公眾號:中科院半導體所】歡迎添加關注!文章轉(zhuǎn)載請注明出處。
發(fā)布評論請先 登錄
相關推薦
簡述你不夠了解的晶振作用
你了解你自已的產(chǎn)品和選用的晶振嗎?
大兄弟啊,你還在擼嗎?
你聽過藍牙的知識產(chǎn)權嗎?關于藍牙的知識產(chǎn)權你了解多少?
頻率和時序,你是否真的了解呢?
你真的了解快充嗎?
學了多年的電路,你真了解晶體管嗎?




















評論